曲线积分：沿着曲线的积分

曲线积分，顾名思义，就是沿着一条曲线进行的积分。与我们常见的定积分（在一段区间上积分）不同，曲线积分的积分路径是一条曲线。

在物理学中，很多问题都可以转化为曲线积分。例如，计算一个力沿一条路径所做的功，计算一个向量场沿一条曲线的环量等等。曲线积分可以用来计算曲线的长度、曲面面积等几何量。

• 第一型曲线积分: 计算一根非均匀密度细杆的总质量。此时，f(x,y)表示细杆在点(x,y)处的线密度，积分结果就是整根细杆的质量。
• 第二型曲线积分: 计算一个物体在变力作用下沿一条曲线移动所做的功。此时，F(x,y)表示作用力，dr表示位移，积分结果就是总功。

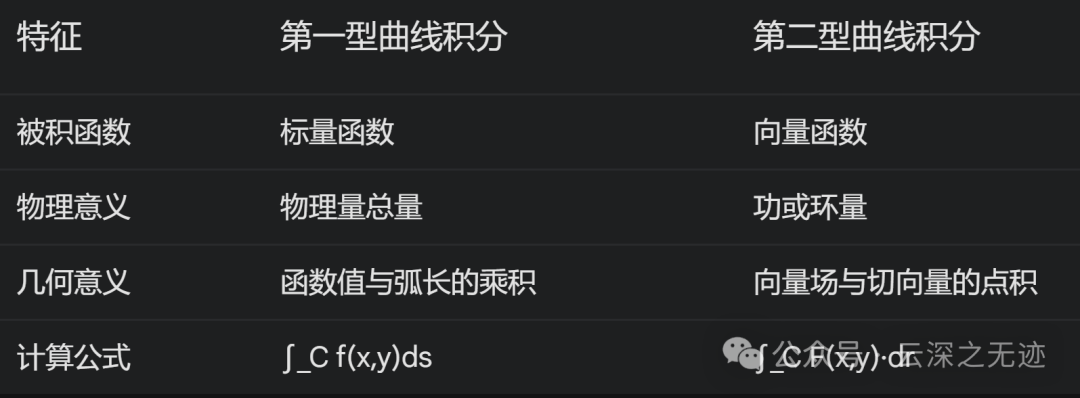
根据被积函数的不同，曲线积分可以分为两类：

第一型曲线积分:

其中，C为积分路径，f(x,y)为被积函数，ds为曲线C上的弧长微元。

被积函数为一个标量函数（即一个数值函数）。

几何意义：表示曲线上的某种物理量（如质量密度、线密度）的总量。在曲线上的函数值与弧长的乘积的累加。

• ∫_C f(x,y)ds

C为积分路径，f(x,y)为被积函数，ds为曲线C上的弧长微元。

第二型曲线积分:

其中，C为积分路径，F(x,y)为向量场，dr为曲线C上的微元向量。

被积函数为一个向量函数。

物理意义：表示一个力场沿一条路径所做的功，或一个向量场沿一条曲线的环量。

• ∫_C F(x,y)·dr

C为积分路径，F(x,y)为向量场，dr为曲线C上的微元向量，·表示向量点积。

• 参数方程法: 将曲线C用参数方程表示，然后将曲线积分转化为定积分。
• 格林公式: 对于闭合曲线上的第二型曲线积分，可以利用格林公式将其转化为二重积分。

格林公式告诉我们，在一定条件下，我们可以将一个闭合曲线的线积分转化为一个平面区域的二重积分。

格林公式将复杂的曲线积分转化为相对简单的二重积分。当曲线积分的计算比较困难时，通过格林公式，我们可以将积分区域转化为平面区域，从而简化计算过程。

设D为平面上的一个简单区域，C是D的正向光滑闭曲线，P(x,y)和Q(x,y)在D上具有连续的一阶偏导数，则有：

∮C Pdx + Qdy = ∬D (∂Q/∂x - ∂P/∂y)dxdy

其中：

• ∮C 表示沿闭曲线C的线积分
• ∬D 表示在区域D上的二重积分
• ∂Q/∂x 和 ∂P/∂y 分别表示函数Q和P对变量x和y的偏导数

格林公式只适用于简单区域和光滑闭曲线。

特别的有当一个第二型曲线积分的值只与路径的起点和终点有关，而与路径的具体形状无关时，我们就说这个曲线积分与路径无关。

从山脚爬到山顶，无论你走的是之字形小路、还是直线登山道，只要起点和终点不变，所做的功（即重力做功）就是一样的。

这就是一个典型的曲线积分与路径无关的例子。

保守力场: 在物理学中，重力、弹力等力被称为保守力。对于保守力场，其对应的曲线积分与路径无关。

全微分: 在数学上，如果一个向量场F(x,y) = P(x,y)i + Q(x,y)j满足条件：

∂Q/∂x = ∂P/∂y

那么向量场F(x,y)就是一个保守场，对应的曲线积分与路径无关。

单连通区域: 积分区域必须是单连通的，即区域内没有“洞”。

混合偏导数相等: 向量场的两个分量函数的混合偏导数相等。

有一个向量场F(x,y) = yi + xj，我们可以验证：

∂Q/∂x = ∂(x)/∂x = 1
∂P/∂y = ∂(y)/∂y = 1

由于∂Q/∂x = ∂P/∂y，所以这个向量场是一个保守场，对应的曲线积分与路径无关。

再次总结