【数据结构与算法】插入排序：原理、实现与分析

一、插入排序 算法简介

在众多排序算法中，插入排序作为一种简单直观的排序方法，虽然在大规模数据集上可能不是最高效的选择，但其独特的优势使得它在某些场景下仍然非常有用。插入排序的基本思想与我们日常生活中整理书籍或卡片的方式非常相似：将未排序的部分逐一取出，然后在已排序的部分中找到合适的位置插入。这种直观的操作方式使得插入排序易于理解和实现，成为学习排序算法时的基础课程。

然而，仅仅掌握插入排序的基本实现是远远不够的。为了在实际应用中更好地利用这一算法，我们还需要深入理解其工作原理、性能特点和应用场景。

————__本文旨在通过详细解析插入排序的原理、实现方式和应用场景，帮助读者全面掌握这一基础但强大的排序算法。我们将从插入排序的基本思想出发，逐步深入到其代码实现、性能分析的探讨中，力求为读者呈现一个全面而深入的插入排序知识体系。

阅读完本篇文章之后，相信你会对插入排序的高级进阶版：希尔排序 感兴趣 可阅读下面文章 【数据结构与算法】希尔排序：基于插入排序的高效排序算法-CSDN博客

二、工作原理

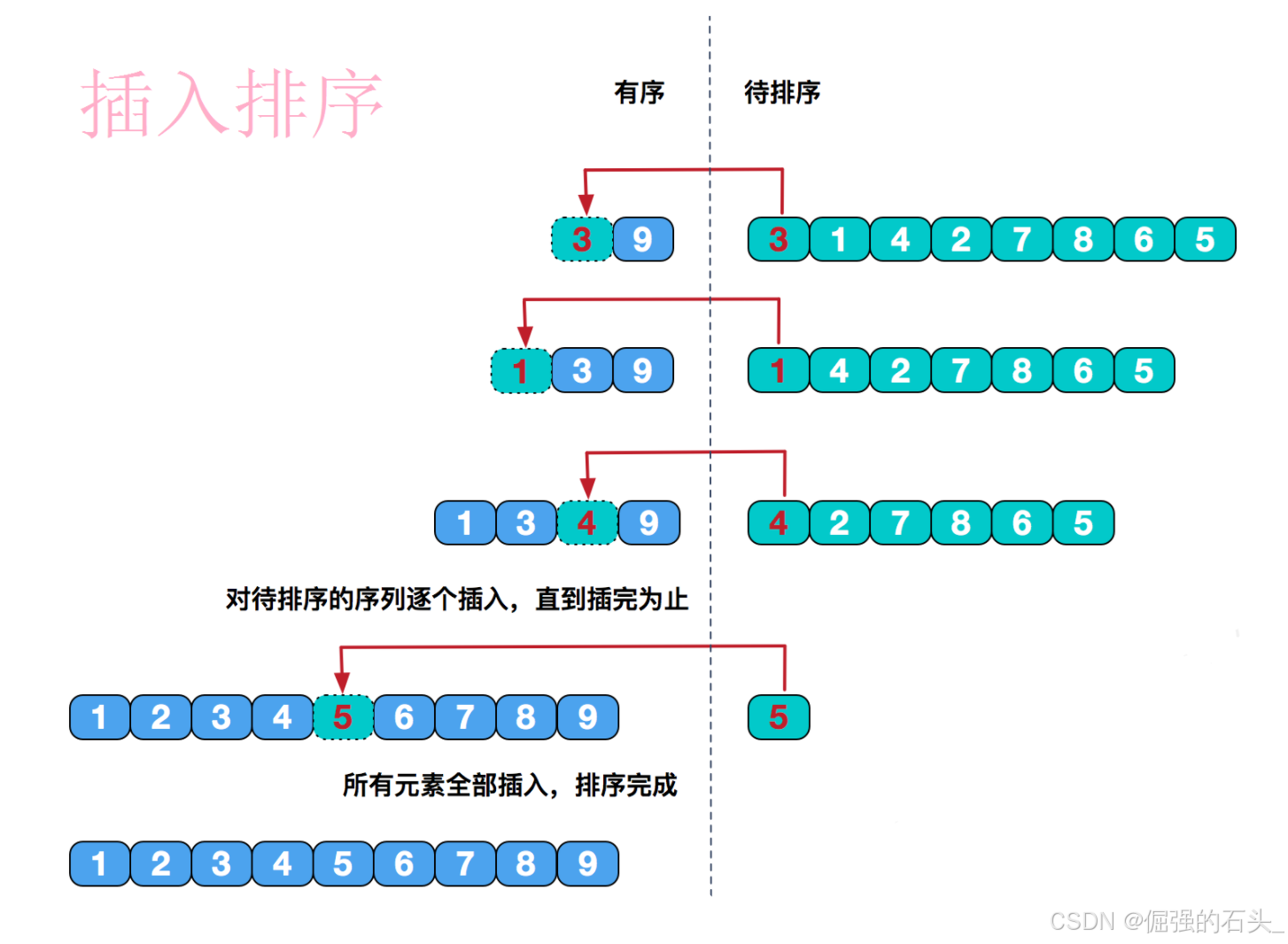
插入排序的基本思想是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据。

三、实现思路

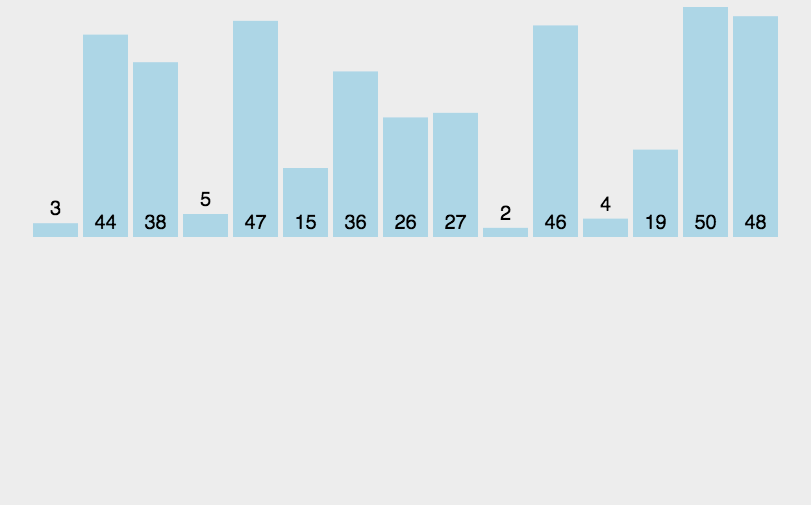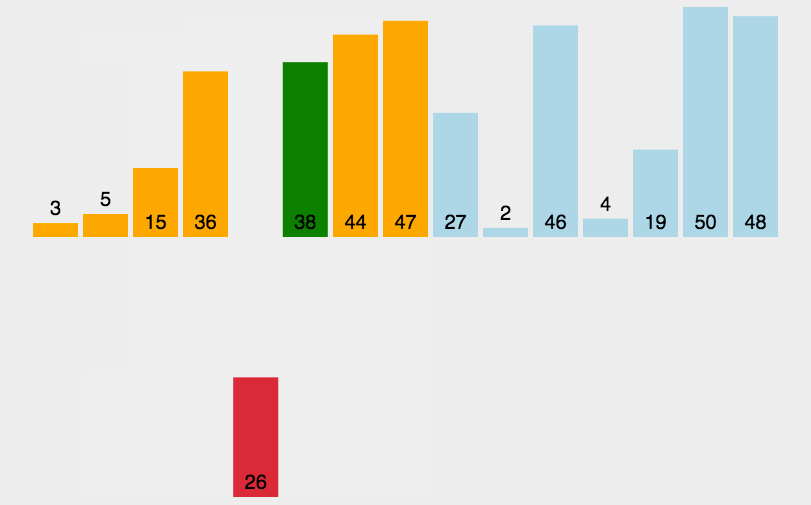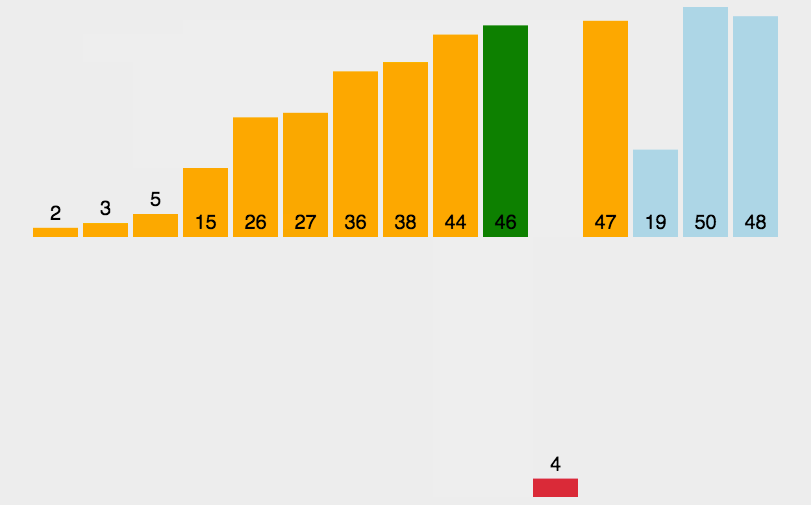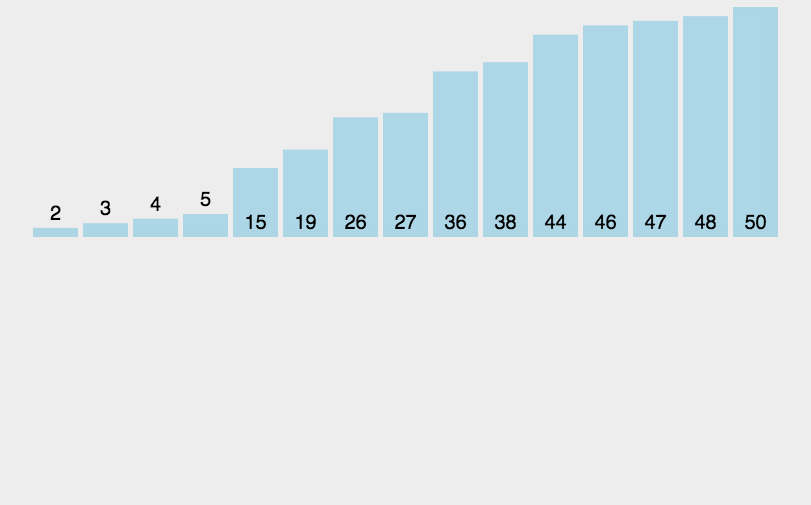
具体步骤是这样的： （以排升序为例）

1. 从第一个元素开始，该元素可以认为已经被排序。
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描。
3. 如果该元素（已排序）大于新元素，将该元素向后移动一位。
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置。
5. 将新元素插入到该位置后。
6. 重复步骤2~5，直到所有元素都排序完成。

四、C语言实现

void InsertSort1(int* a, int n)//升序
{
	for (int i = 1; i <= n-1 ; i++)//控制要插入的元素个数
	{
		int key = a[i];
		int end = i - 1;
		while (end >= 0 && a[end] > key)//移动元素
		{
			a[end + 1] = a[end];
			end--;
		}
		a[end+1] = key;//满足大小关系后插入到指定位置
	}
}
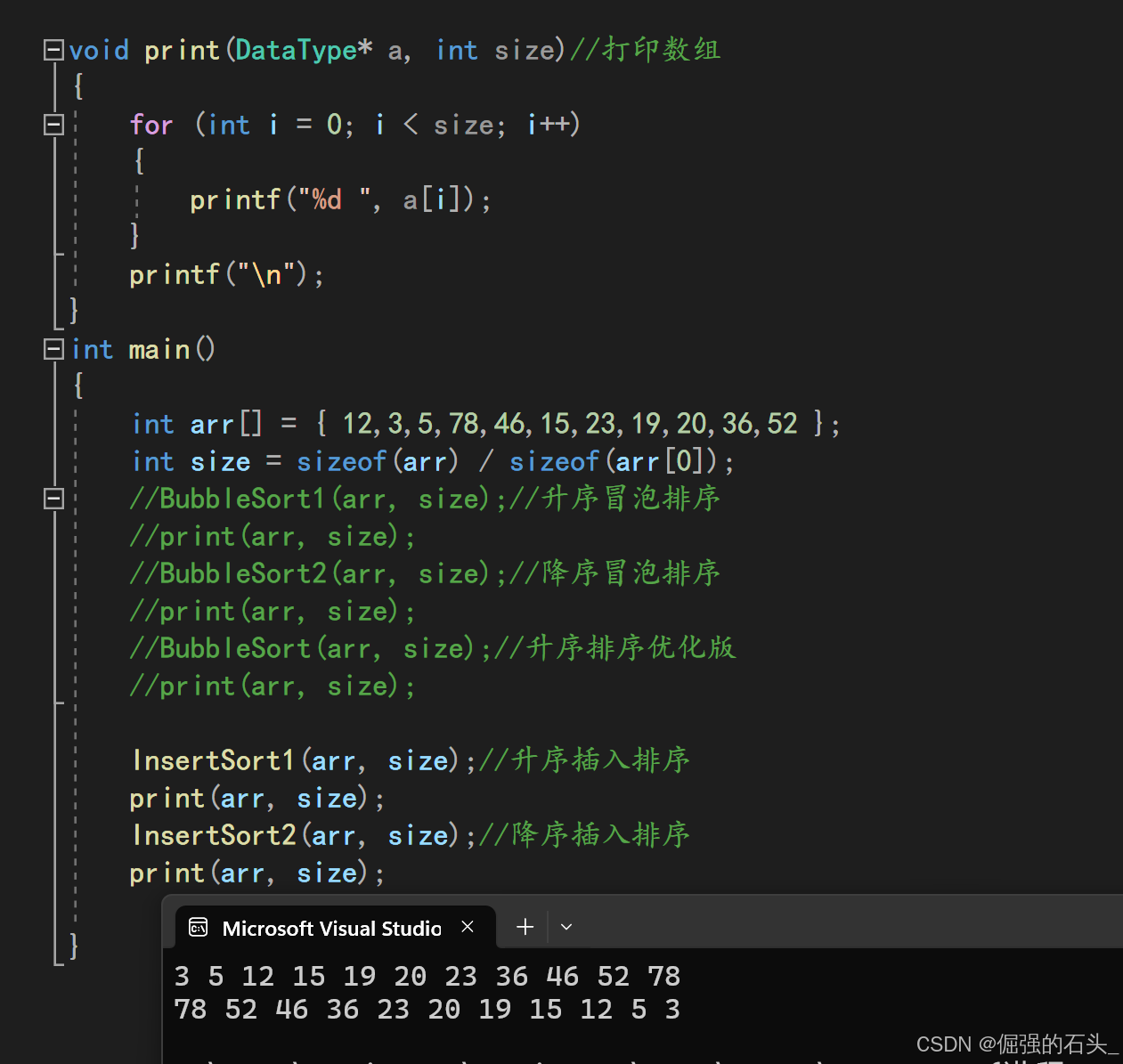
void InsertSort2(int* a, int n)//降序
{
	for (int i = 1; i <= n - 1; i++)//控制要插入的元素个数
	{
		int key = a[i];
		int end = i - 1;
		while (end >= 0 && a[end] < key)//移动元素
		{
			a[end + 1] = a[end];
			end--;
		}
		a[end + 1] = key;//满足大小关系后插入到指定位置
	}
}

五、性能分析

🍃时间复杂度：O(n^2)

最好情况（O(n)）： 当输入数组已经是排序状态时，插入排序的性能最优。此时，每个元素只需与其前面的一个元素进行比较（因为它已经位于正确的位置），因此总共需要进行大约n-1次比较，时间复杂度为O(n)。这里的n是数组的长度。 最坏情况（O(n^2)）： 当输入数组完全逆序时，插入排序的性能最差。对于每个元素，都需要与其前面的所有元素进行比较，直到找到合适的位置。因此，第i个元素需要比较i次（其中i从2开始，直到n），总共需要进行的比较次数大约为1 + 2 + 3 + ... + (n-1) = n(n-1)/2，时间复杂度为O(n^2)。 平均情况（O(n^2)）： 对于随机排列的数组，插入排序的平均时间复杂度也是O(n^2)。这是因为大部分情况下，元素都需要进行多次移动和比较才能找到正确的位置。

🍃空间复杂度：O(1)

插入排序是一种原地排序算法，它只需要一个额外的存储空间来暂存当前需要插入的元素（即“key”），而不需要额外的数组来存储排序过程中的数据。因此，其空间复杂度为O(1)。

🍃稳定性：稳定算法

插入排序是一种稳定的排序算法。在插入排序过程中，如果两个相等的元素，后面的元素不会移动到前面元素的前面，而是直接插入到与它相等的元素之后，从而保持了原有的相对顺序。

六、应用场景

插入排序虽然在大规模数据集上可能不是最高效的排序算法，但其简单性、稳定性和在某些特定场景下的高效性使得它在许多实际应用中仍然具有一定的价值。

• 小规模数据集：由于插入排序在小规模数据集上表现良好，且实现简单，因此常用于对少量数据进行排序的场景。
• 几乎有序的数据集：当数据已经接近有序时，插入排序的性能会显著提高。因为此时大部分元素已经处于或接近其最终位置，所需的比较和移动次数会大幅减少。
• 链表排序：由于链表不支持像数组那样的随机访问，因此在链表上进行排序时，插入排序成为了一个非常合适的选择。它可以通过改变节点的指针来实现元素的移动，而不需要额外的存储空间。