【深度学习】Pytorch 系列教程（六）：PyTorch数据结构：2、张量的数学运算（4）：一维卷积及其数学原理（步长stride、零填充pad；宽卷积、窄卷积、等宽卷积；卷积运算与互相关运算）

Qomolangma

发布于 2025-06-02 12:17:48

19000

代码可运行

文章被收录于专栏：深度学习深度学习

运行总次数：0

代码可运行

一、前言

卷积运算是一种在信号处理、图像处理和神经网络等领域中广泛应用的数学运算。在图像处理和神经网络中，卷积运算可以用来提取特征、模糊图像、边缘检测等。在信号处理中，卷积运算可以用来实现滤波器等操作。本文将介绍一维卷积运算，包括步长、零填充；宽卷积、窄卷积、等宽卷积；卷积运算与互相关运算等及其PyTorch实现。

二、实验环境

本系列实验使用如下环境

conda create -n DL python==3.11

conda activate DL

conda install pytorch torchvision torchaudio pytorch-cuda=12.1 -c pytorch -c nvidia

三、PyTorch数据结构

1、Tensor（张量）

Tensor（张量）是PyTorch中用于表示多维数据的主要数据结构，类似于多维数组，可以存储和操作数字数据。

1. 维度（Dimensions）

Tensor（张量）的维度（Dimensions）是指张量的轴数或阶数。在PyTorch中，可以使用size()方法获取张量的维度信息，使用dim()方法获取张量的轴数。

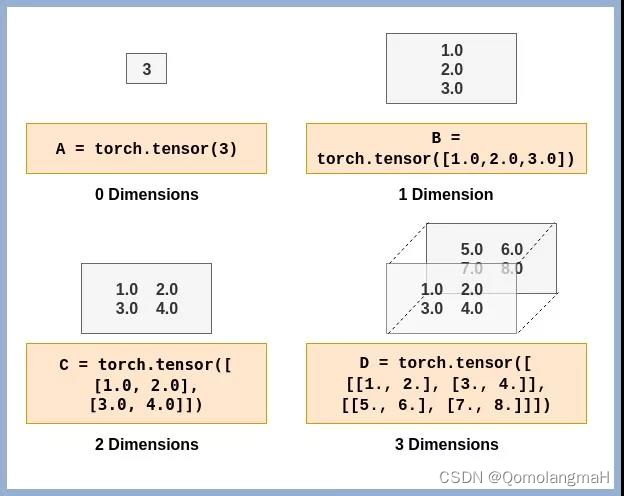
2. 数据类型（Data Types）

PyTorch中的张量可以具有不同的数据类型：

torch.float32或torch.float：32位浮点数张量。
torch.float64或torch.double：64位浮点数张量。
torch.float16或torch.half：16位浮点数张量。
torch.int8：8位整数张量。
torch.int16或torch.short：16位整数张量。
torch.int32或torch.int：32位整数张量。
torch.int64或torch.long：64位整数张量。
torch.bool：布尔张量，存储True或False。

【深度学习】Pytorch 系列教程（一）：PyTorch数据结构：1、Tensor（张量）及其维度（Dimensions）、数据类型（Data Types）

3. GPU加速（GPU Acceleration）

【深度学习】Pytorch 系列教程（二）：PyTorch数据结构：1、Tensor（张量）： GPU加速（GPU Acceleration）

2、张量的数学运算

PyTorch提供了丰富的操作函数，用于对Tensor进行各种操作，如数学运算、统计计算、张量变形、索引和切片等。这些操作函数能够高效地利用GPU进行并行计算，加速模型训练过程。

4. 一维卷积运算

卷积运算是一种在信号处理、图像处理和神经网络等领域中广泛应用的数学运算。在图像处理和神经网络中，卷积运算可以用来提取特征、模糊图像、边缘检测等。在信号处理中，卷积运算可以用来实现滤波器等操作。

a. 数学原理

在离散的情况下，给定两个函数

f(n)

和

g(n)

，它们的卷积运算定义为：

(f * g)(n) = \sum_{i} (f(i) \cdot g(n-i))

这里的

代表卷积运算，

代表离散的变量。具体地，

f(n)

和

g(n)

的卷积运算

(f * g)(n)

表示在

位置上的加权求和，其中每个加权项是

f(i)

和

g(n-i)

的乘积，

是自由变量。

在连续的情况下，给定两个函数

f(x)

和

g(x)

，它们的卷积运算定义为：

(f * g)(x) = \int f(u) \cdot g(x-u) du

这里的

代表连续的变量。具体地，

f(x)

和

g(x)

的卷积运算

(f * g)(x)

表示在

位置上的加权积分，其中每个加权项是

f(u)

和

g(x-u)

的乘积，

是自由变量。

在图像处理和神经网络中，卷积运算通常是在离散的情况下进行的。卷积运算的主要特点是具有移动不变性和线性性质，这使得它在信号处理和图像处理中具有广泛的应用。

b. 一维卷积

基于卷积的定义，给定长度为

的输入信号

和长度为

的卷积核（或滤波器）

，一维离散卷积操作可以表示为：

(x * h)[n] = \sum_{k=0}^{N-1} x[k] \cdot h[n-k]

其中，

x[k]

表示输入信号的第

个元素，

h[n-k]

表示卷积核的第

n-k

个元素。

计算步骤：

对输入信号x和卷积核h进行对齐，即将卷积核h翻转180度；
将卷积核h从输入信号x的左端开始，依次与输入信号进行元素级乘法并累加求和，得到卷积输出的第n个元素;

在深度学习中，一维卷积常被用于处理时序数据，例如语音识别、文本分类等任务。同时，一维卷积操作也是构建一维卷积神经网络（1D-CNN） 的基础，通过多层一维卷积层和池化层的堆叠，可以提取输入时序数据中的特征。

步长

步长（stride）是指卷积核在进行卷积操作时在输入信号上滑动的步长大小。在一维卷积中，如果步长为1，则卷积核每次只移动一个元素进行卷积操作；如果步长为2，则卷积核每次移动两个元素进行卷积操作，以此类推。调整步长可以影响输出信号的长度，以及最终卷积后的特征提取效果。较大的步长可以减少输出信号的长度，同时减少特征提取时的重叠部分，而较小的步长则可以保留更多输入信号的信息。

零填充

零填充（zero-padding）是一种在进行卷积操作时在输入信号的两侧（或者一个侧）填充零值的技术。填充的目的是为了调整卷积操作后输出信号的长度，以及保持输入输出信号的对齐性。

宽卷积、窄卷积、等宽卷积

卷积的结果按输出长度不同可以分为三类（输入向量的长度M，卷积核的长度K）：

窄卷积（Narrow Convolution）
- 步长 𝑇 = 1，两端不补零 𝑃 = 0
- 卷积后输出长度为 𝑀 − 𝐾 +1
宽卷积（Wide Convolution）
- 步长 𝑇 = 1，两端补零 𝑃 = 𝐾 -1
- 卷积后输出长度为 𝑀 + 𝐾 - 1
等宽卷积（Same Convolution）
- 步长 𝑇 = 1，两端补零 𝑃 = (𝐾 -1) / 2
- 卷积后输出长度为 𝑀
注意：
- 在早期的文献中，卷积一般默认为窄卷积；而目前的文献中，一般默认为等宽卷积。

c. nn.Conv1d函数

在PyTorch中，使用nn.Conv1d计算一维卷积，其期望的输入是一个三维张量，具有以下维度：[batch_size, in_channels, input_length]。同样，卷积核也需要转换成合适的维度。一般来说，卷积操作期望输入信号和卷积核的维度满足这种规范。

batch_size表示一次输入的样本数量，通常情况下使用1。
in_channels表示输入信号的通道数。
input_length表示输入信号的长度。

因此需要使用.view(1, 1, -1)将输入信号和卷积核转换成了这种期望的维度格式。

第一个参数1表示batch size为1。
第二个参数1表示通道数为1。
第三个参数-1表示PyTorch会根据张量的总元素数自动计算最后一个维度的大小，这里用于自动计算输入信号的长度。

import torch
import torch.nn as nn


input_signal = torch.tensor([1, 1, 2, -1, 1, -3, 1], dtype=torch.float)
# conv_kernel = torch.tensor([1/3, 1/3, 1/3])
conv_kernel = torch.tensor([-1, 0, 1], dtype=torch.float)
conv_kernel = torch.flip(conv_kernel, [0])
print(f"原始维度:{conv_kernel.size()}")
print(f"原始轴数:{conv_kernel.dim()}")

# 将输入信号和卷积核转换成合适的维度
input_signal = input_signal.view(1, 1, -1)
conv_kernel = conv_kernel.view(1, 1, -1)
print(f"转换后维度:{conv_kernel.size()}")
print(f"转换后轴数:{conv_kernel.dim()}")
# conv_kernel = torch.flip(conv_kernel, [0])
# print(f"conv_kernel:{conv_kernel}")

M = input_signal.size(-1)
K = conv_kernel.size(-1)
# 创建宽、窄、等宽卷积层
conv1d_wide = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=K, padding=K - 1, bias=False)
conv1d_narrow = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=K, bias=False)
conv1d_same = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=K, padding=int((K - 1) / 2), bias=False)
conv1d_stride2 = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=K, stride=2, bias=False)

# 将卷积核加载到卷积层中
conv1d_wide.weight.data = conv_kernel
conv1d_narrow.weight.data = conv_kernel
conv1d_same.weight.data = conv_kernel
conv1d_stride2.weight.data = conv_kernel

output_wide = conv1d_wide(input_signal)
print(f"宽卷积:\n\t{output_wide}")
output_same = conv1d_same(input_signal)
print(f"等宽卷积:\n\t{output_same}")
output_narrow = conv1d_narrow(input_signal)
print(f"窄卷积:\n\t{output_narrow}")
output_stride2 = conv1d_stride2(input_signal)
print(f"步长=2窄卷积:\n\t{output_stride2}")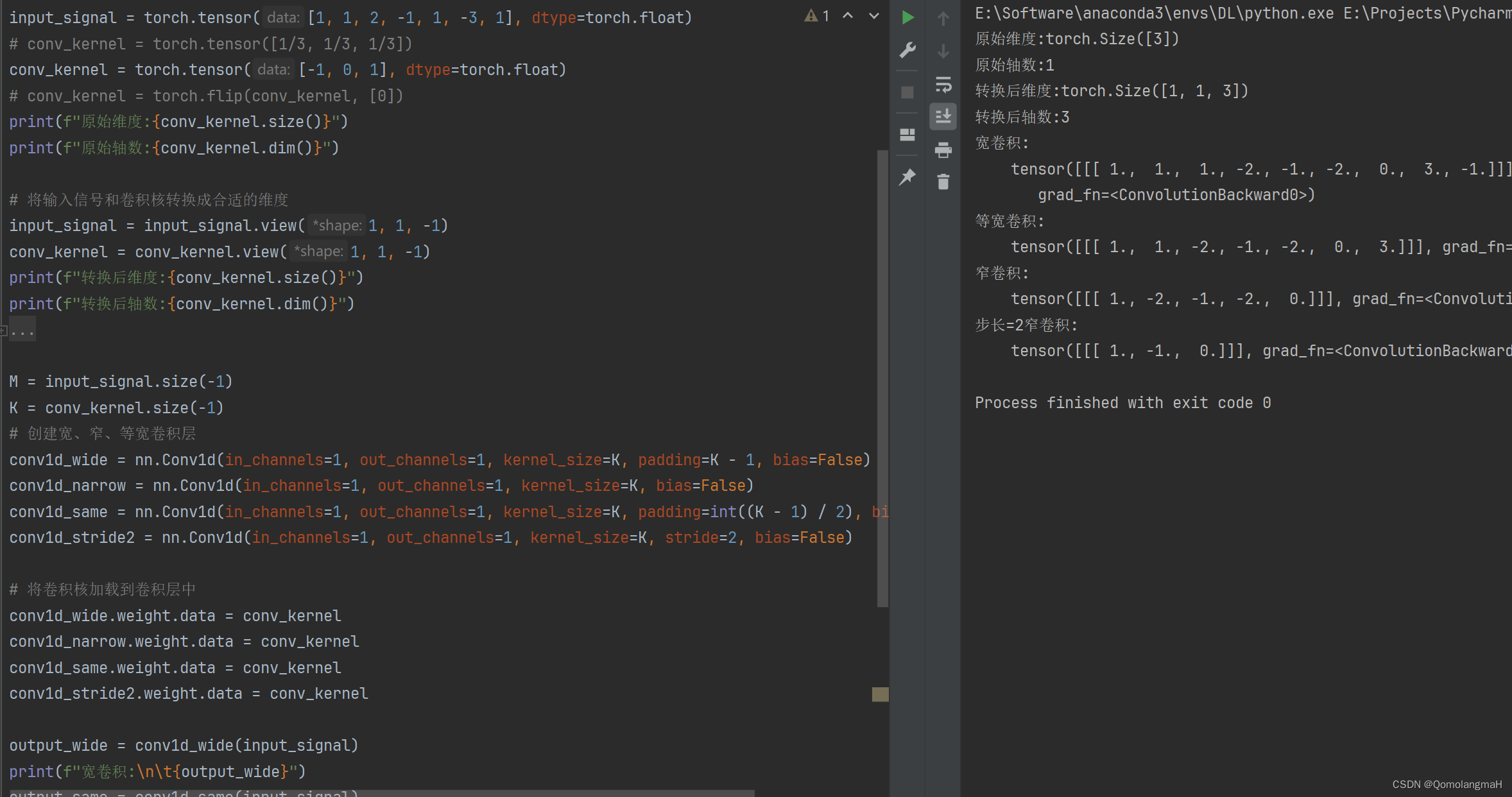

d. 互相关

注意：在神经网络中使用卷积是为了进行特征抽取，卷积核是否进行翻转和其特征抽取的能力无关（互相关和卷积的区别也可以理解为图像是否进行翻转）。特别是当卷积核是可学习的参数时，卷积和互相关在能力上是等价的。因此，为了实现上（或描述上）的方便起见，我们用互相关来代替卷积。事实上，很多深度学习工具中卷积操作其实都是互相关操作，如上图PyTorch计算结果即为互相关。

翻转卷积核，计算结果与前面手动计算结果相同：

conv_kernel = torch.flip(conv_kernel, [0])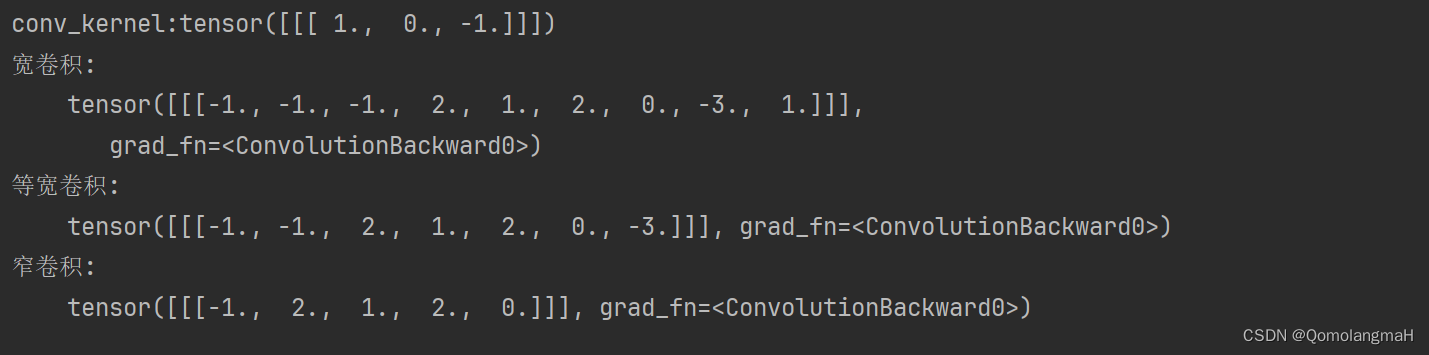

d. torch.nn.functional.conv1d

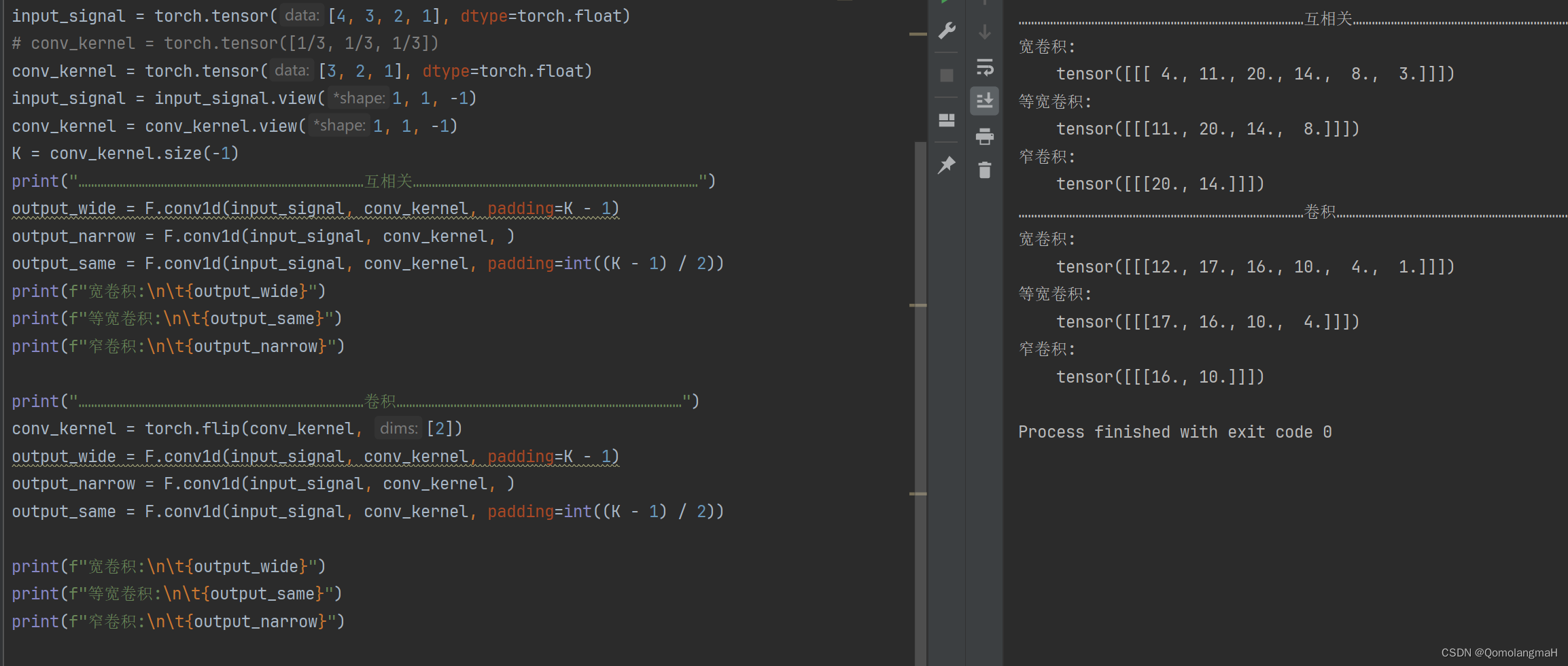
import torch
import torch.nn.functional as F

input_signal = torch.tensor([1, 1, 2, -1, 1, -3, 1], dtype=torch.float)
# conv_kernel = torch.tensor([1/3, 1/3, 1/3])
conv_kernel = torch.tensor([-1, 0, 1], dtype=torch.float)
input_signal = input_signal.view(1, 1, -1)
conv_kernel = conv_kernel.view(1, 1, -1)
K = conv_kernel.size(-1)
print("………………………………………………………………………………互相关………………………………………………………………………………")
output_wide = F.conv1d(input_signal, conv_kernel, padding=K - 1)
output_narrow = F.conv1d(input_signal, conv_kernel, )
output_same = F.conv1d(input_signal, conv_kernel, padding=int((K - 1) / 2))
print(f"宽卷积:\n\t{output_wide}")
print(f"等宽卷积:\n\t{output_same}")
print(f"窄卷积:\n\t{output_narrow}")

print("………………………………………………………………………………卷积………………………………………………………………………………")
conv_kernel = torch.flip(conv_kernel, [2])
output_wide = F.conv1d(input_signal, conv_kernel, padding=K - 1)
output_narrow = F.conv1d(input_signal, conv_kernel, )
output_same = F.conv1d(input_signal, conv_kernel, padding=int((K - 1) / 2))

print(f"宽卷积:\n\t{output_wide}")
print(f"等宽卷积:\n\t{output_same}")
print(f"窄卷积:\n\t{output_narrow}")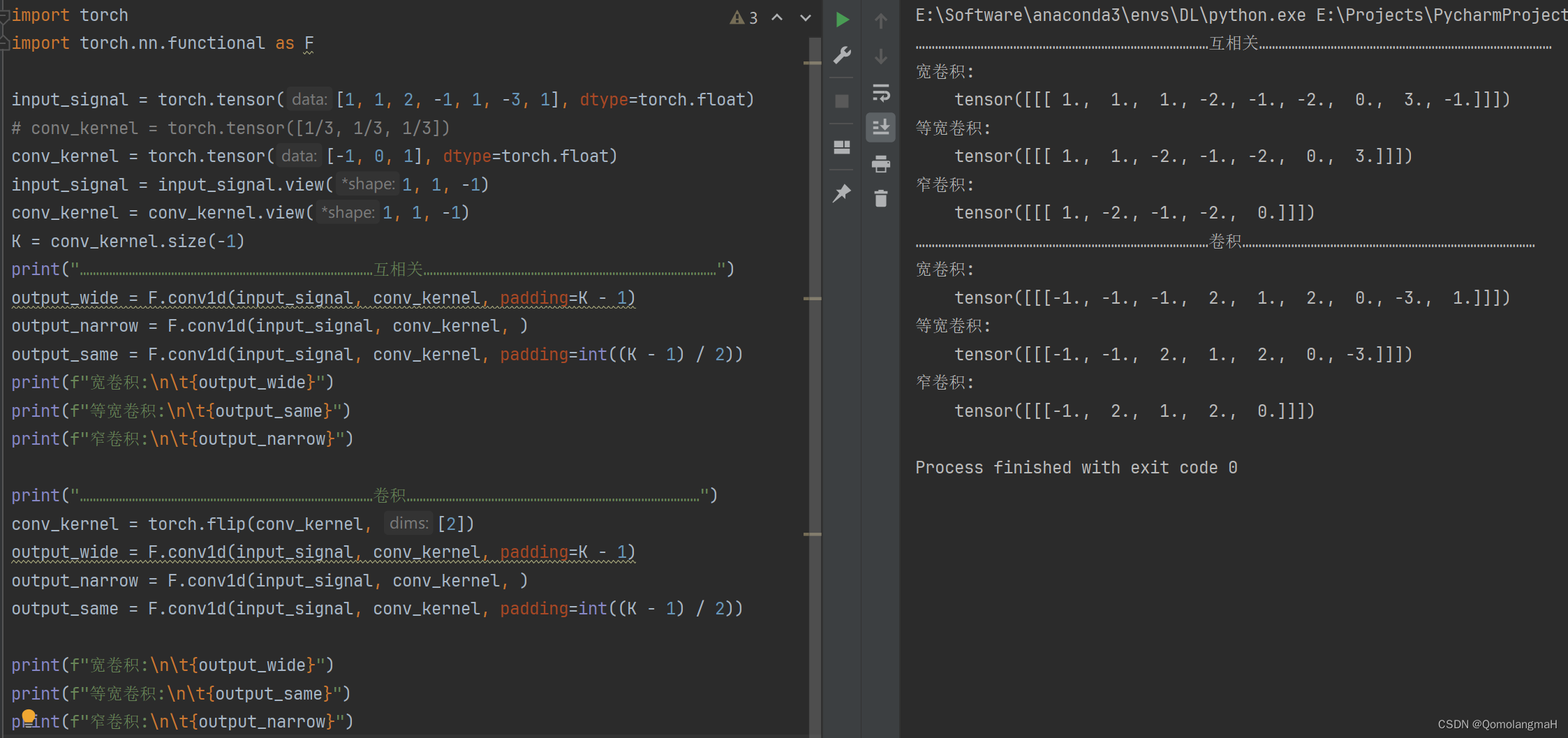

注意：卷积与互相关不是相反数关系，上述卷积核-1, 0, 1特殊~

e. torch.nn.functional.pad

import torch


input_signal = torch.tensor([1, 1, 2, -1, 1, -3, 1], dtype=torch.float)
conv_kernel = torch.tensor([-1, 0, 1], dtype=torch.float)

# 反转卷积核~定义
conv_kernel_flipped = torch.flip(conv_kernel, [0])
K = conv_kernel.numel()
print(f"K:{K}")
# 零填充输入信号
padded_input = torch.nn.functional.pad(input_signal, (K - 1, K - 1), 'constant', 0)
print(f"输入信号:{padded_input}")
# 执行卷积运算
output1 = torch.nn.functional.conv1d(padded_input.view(1, 1, -1), conv_kernel_flipped.view(1, 1, -1))
# 输出结果
print(f"卷积运算:{output1}")
# 互相关运算
output2 = torch.nn.functional.conv1d(padded_input.view(1, 1, -1), conv_kernel.view(1, 1, -1))
# 输出结果
print(f"互相关运算:{output2}")

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-01-09，如有侵权请联系 cloudcommunity@tencent.com 删除

pytorch

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度