【数据结构】考研408｜从B树到B+树：多路平衡的优化形态与数据库索引基石

(B+树)

B+树

导读

大家好，很高兴又和大家见面啦！！！ 在前面的内容中我们对 B树 进行了深入的探讨： B树 可以是一棵空树，也可以是一棵满足以下性质的 m叉树：

• 树中的每个结点最多有 m 棵子树，结点中最多有 m - 1 个关键字
• 若根结点不是叶结点，则根结点至少有 2 棵子树，即至少有 1 个关键字
• 除根节点外，其余所有的非叶结点至少有 \lceil \frac{m}{2} \rceil 棵子树，即至少有 \lceil \frac{m}{2} \rceil - 1 个关键字
• 所有的 叶结点 均位于同一层次上，且不携带任何信息（叶结点 也可称为 空叶结点、外部结点 或 失败结点）

B树 作为一棵最经典的 多路平衡查找树，通过 分裂 、借位、合并等操作实现了其动态操作时的 绝对平衡 在 B树 中，其 树高 与 磁盘存取次数 成正比，通过深入的探讨，我们得到了其树高 h 与结点数量 n 以及分支数量 m 之间的关系：

尽管 B树 本身设计精妙，但在实际数据库应用中，它逐渐暴露出一些局限性。例如：

• B树 在进行范围查询（如查找5到50之间的所有数据）时效率较低。因为在 B树 中找到范围的起始点（如5）之后，无法直接、连续地访问下一个关键字，往往需要回溯到父节点再进入其他子树进行查找，这个过程会产生大量的随机磁盘I/O操作
• B树的结点既存储数据又存储指针，导致空间利用率相对较低，且节点分裂和合并操作较为复杂，维护成本较高。

这些局限性促使数据库系统寻找更优化的索引结构，于是 B+树 应运而生。 那么，B+树 具体是如何解决 B树 的这些痛点的？它的设计又有哪些精妙之处？接下来，就让我们一起进入 B+树 的精彩世界，探索这一数据库索引核心技术的奥秘。

一、基本概念

B+树 是应数据库所需而出现的一种 B树 的变形树。

1.1 定义

一棵 m阶B+树 应满足以下条件：

• 每个分支结点最多有 m 棵子树
• 非叶根结点至少有两颗子树，其他每个分支结点至少有 \lceil \frac{m}{2} \rceil 棵子树
• 结点的子树个数与关键字个数相等
• 所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序相互链接起来（支持顺序查找）
• 所有分支结点（可视为索引的索引）中仅包含它的各个子结点（下一级的索引块）中关键字的最大值及指向其子结点的指针

1.2 B+树的结构

B+树 我们可以将其视为一棵 多路分块查找树 。 在说明 B+树 之前，我们先简单的回顾一下 分块查找：

• 分块查找 又称为 索引顺序查找
  • 核心思想：通过将查找的关键字进行分块，并通过分块中的最大值建立相应的索引表，我们可以通过索引表来快速的确定具体的分块，之后再对分块进行顺序查找

分块查找 通过 块内无序，块间有序 的设计思想平衡了顺序查找的动态性与查找效率；

相信有部分朋友可能已经忘记了什么是 分块查找 ，存在疑惑的朋友可以点击链接，回顾一下其具体内容。

B+树 正是采用了 分块查找 的索引思路：

• B+树 中的每一个结点就是一个 块
• 每个结点中会存储 [\lceil \frac{m}{2} \rceil, m] 个关键字
• 每个结点中的关键字的最大值会作为索引存储在其父结点中
• 除了 终端结点 外，其他结点中的关键字仅作为 索引值

这里我们以一棵 4阶B+树 为例进行说明：

flowchart TB
	subgraph 索引值
		a[60, 85]
		b[10, 20, 50, 60]
		c[77, 85]
	end
a--->b
a--->c
	subgraph 数据信息
		d[8, 10]
		e[16, 20]
		f[40, 50]
		g[55, 60]
		h[69, 77]
		i[80, 85]
	end
b--->d
b--->e
b--->f
b--->g

c--->h
c--->i

在 B+树 中，根据关键字的具体功能，我们可以将树分为两部分：

• 索引部分：只负责索引的 根结点 和其他 非叶结点
• 数据部分：负责存储数据信息的 叶子结点 也可以称之为 终端结点

1.2.1 索引部分

在索引部分中，关键字只负责指示下一层的结点具体位置。 就比如根结点中的关键字 60 只负责指示下一层的结点为 左侧子树 ，且子树中的最大值为 60 ；关键字 85 只负责指示下一层的结点为 右侧子树，且子树中的最大值为 85；

flowchart TB
	subgraph 索引值
		a[60, 85]
		b[10, 20, 50, 60]
		c[77, 85]
	end
a--->b
a--->c
	subgraph 数据信息
		d[8, 10]
		e[16, 20]
		f[40, 50]
		g[55, 60]
		h[69, 77]
		i[80, 85]
	end
b--->d
b--->e
b--->f
b--->g

c--->h
c--->i

classDef R color: white, fill: red, stroke: red, stroke-width: 2px
class a R

以关键字 60 为例，我们通过该关键字以及该关键字对应的指针，能够找到具体的子树：

flowchart TB
	subgraph 索引值
		b[10, 20, 50, 60]
	end
	subgraph 数据信息
		d[8, 10]
		e[16, 20]
		f[40, 50]
		g[55, 60]
	end
b--->d
b--->e
b--->f
b--->g

classDef R color: white, fill: red, stroke: red, stroke-width: 2px
class b R

在该子树中，其根节点仍为 索引部分 ，因此根节点中存储的关键字仍然只负责进行索引，且结点中的每一个关键字均对应着一棵子树；

1.2.2 数据部分

我们通过索引部分的索引值以及索引值对应的指针，最终能够找到目标关键字所在的 叶子结点，通过叶子结点中的关键字以及对应的指针，我们能够获取对应的全部数据信息； 比如我们要在上述的 B+树 中查找关键字 10 ，通过索引部分，我们最终能够确定该关键字所在的 终端结点：

flowchart TB
	subgraph Node[终端结点]
		direction TB
		a[8<br>ptr]
		b[10<br>ptr]
	end
	a--->data1[数据记录1]
	b--->data2[数据记录2]

classDef R color: white, fill: red, stroke: red, stroke-width: 2px
class b R
class data2 R

在该结点中，每个关键字均会对应一个指向 数据记录 的指针，我们通过目标关键字的指针就能够读取相应的数据信息；

1.2.3 顺序链表

在 B+树 中，除了能够通过索引值进行索引查找的 索引查找树 之外，同时还存在一个能够进行 顺序查找 的 链表：

flowchart LR
	subgraph T[数据部分]
		d[8, 10]
		e[16, 20]
		f[40, 50]
		g[55, 60]
		h[69, 77]
		i[80, 85]
	end
	ptr ---> d ---> e ---> f ---> g ---> h ---> i

该 链表 就是由 索引树 中的 叶子结点 组成，我们可以通过指针 ptr 对该部分中的内容进行 顺序查找 ，在找到目标关键字后，我们可以继续通过其对应的指针来读取相应的数据信息；

1.3 B+树的形态

完整的 B+树 可以视为两部分：

• 索引树部分：索引树由 索引部分 和 数据部分 组成

flowchart TB
	subgraph 索引值
		direction TB
		a[60, 85]
		b[10, 20, 50, 60]
		c[77, 85]
	end
a--->b
a--->c
	subgraph 数据信息
		direction LR
		subgraph N1[叶子1]
			direction TB
			d1[8<br>ptr]
			d2[10<br>ptr]
		end
		subgraph N2[叶子2]
			direction TB
			e1[16<br>ptr]
			e2[20<br>ptr]
		end
		subgraph N3[叶子3]
			direction TB
			f1[8<br>ptr]
			f2[10<br>ptr]
		end
		subgraph N4[叶子4]
			direction TB
			g1[16<br>ptr]
			g2[20<br>ptr]
		end
		subgraph N5[叶子5]
			direction TB
			h1[8<br>ptr]
			h2[10<br>ptr]
		end
		subgraph N6[叶子6]
			direction TB
			i1[16<br>ptr]
			i2[20<br>ptr]
		end
	end
b--->N1
b--->N2
b--->N3
b--->N4

c--->N5
c--->N6

	subgraph Cord[数据记录]
		cord1[记录1]
		cord2[记录2]
		cord3[记录3]
		cord4[记录4]
		cord5[记录5]
		cord6[记录6]
		cord7[记录7]
		cord8[记录8]
		cord9[记录9]
		cord10[记录10]
		cord11[记录11]
		cord12[记录12]
	end
	d1--->cord1
	d2--->cord2
	e1--->cord3
	e2--->cord4
	f1--->cord5
	f2--->cord6
	g1--->cord7
	g2--->cord8
	h1--->cord9
	h2--->cord10
	i1--->cord11
	i2--->cord12
classDef R color: white, fill: red, stroke: red, stroke-width: 2px

• 链表部分：链表部分由 数据部分 组成

flowchart LR
	subgraph T[数据部分]
		direction LR
		d[8, 10]
		e[16, 20]
		f[40, 50]
		g[55, 60]
		h[69, 77]
		i[80, 85]
	end
	ptr ---> d ---> e ---> f ---> g ---> h ---> i

在该链表中，每个结点中的每个关键字都会对应一个记录：

flowchart TB
	subgraph 结点
		direction TB
		data1[key1<br>ptr] 
		data2[key2<br>ptr] 
	end
	data1 ---> cord1[记录1]
	data2 ---> cord2[记录2]

当我们将二者结合，就得到了一棵完整的 B+树：

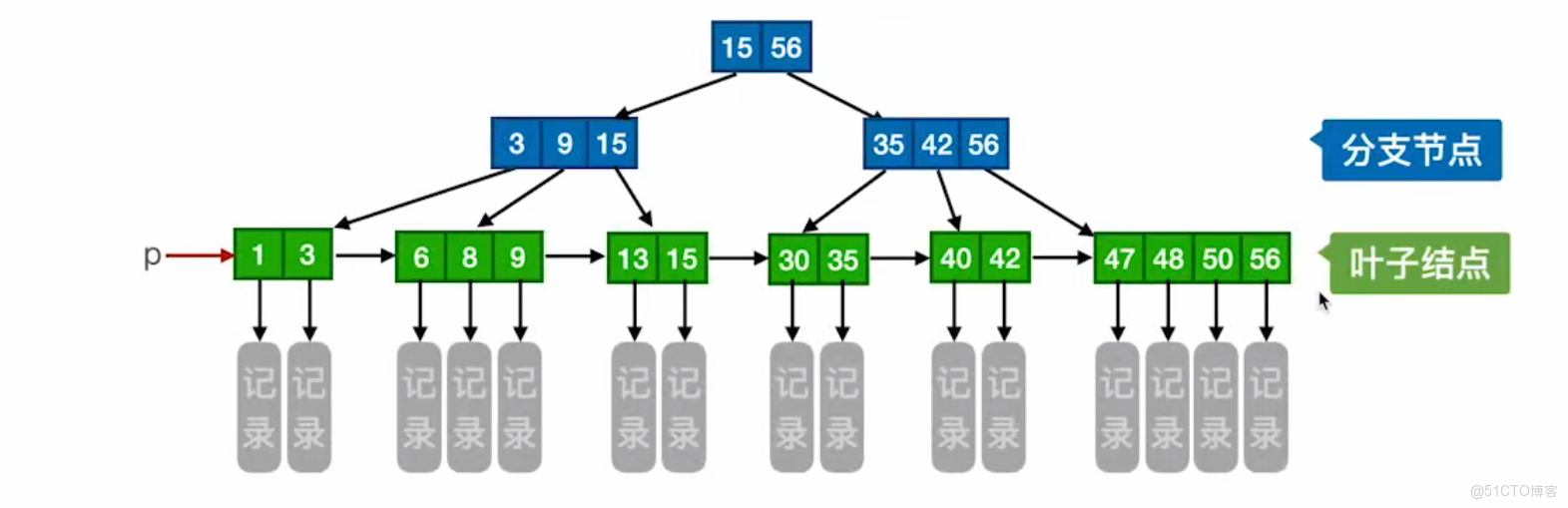
B+树.png

二、两种视角

根据 B+树 的索引部分的结点中关键字的作用，存在着两种不同视角下的 B+树：

• 教学视角：关键字作为“子树代表”
• 算法视角：关键字作为“分界值”

在前面的介绍中，我们就是从 教学视角 出发，在学习 B+树 的基本定义。在该视角下，索引部分中的关键字是作为其子树的代表，因此一个关键字就对应着一棵子树，这也就得到了 结点的子树个数与关键字个数相等 这条性质； 而我们在具体的实现中，通常使用的是 算法视角，这是《算法导论》、数据库系统教材（如《Database System Concepts》）采用的算法定义，是数据库引擎实际实现的基础。 在 算法视角 下，B+树 索引部分的关键字作用与 B树 一样，均是作为子树的分界值：

• 一个关键字对应着两棵子树：
  • 左子树中，关键字的值不大于 分界值
  • 右子树中，关键字的值不小于 分界值

就比如我们可以采用：左子树 <$``$\leq 右子树 ，这一定义来构建一棵 B+树：

flowchart TB
a[key1, key2]
b[key3, key4]
c[key1, key5, key6]
d[key2, key7, key8]
a--->b
a--->c
a--->d

当然我们也可以采用：左子树 \leq 分界值 <

flowchart TB
a[key1, key2]
b[key3, key4, key1]
c[key5, key6, key2]
d[key7, key8]
a--->b
a--->c
a--->d

不管是上述的哪种定义，在 算法视角 中，作为索引的关键字均是作为子树的 分界值。因此，在该视角中，结点的子树个数 == 关键字个数 + 1 ； 算法视角 实际上就是严格意义上的基于 B树 的一棵变形树，该视角下的 B+树 与 教学视角 下的 B+树 的核心一致：

• 非叶结点中的关键字仅作为 索引值
• 所有数据 仅存于 叶子结点
• 叶子结点形成 有序链表

算法视角（子树指针数 = 关键字数 + 1）是国际学术界和工业界在形式化定义、算法描述及系统实现中最为通行的标准。而 教学视角（子树数 = 关键字数）是一种广泛使用、非常有效的教学可视化工具。因此，无论采用的是哪种视角，我们只需要抓住 B+树 的核心即可。 接下来我们就从 教学视角 出发，一起来探讨一下 B+树 与 B树 之间的差异；

三、B树与B+树的差异

同样是 多路查找树 家族中的一员，B树 与 B+树 之间还是存在不少差异：

• 子树个数与关键字个数对应关系不同： B树 中，n 个关键字对应 n + 1 棵子树 B+树 中，n 个关键字对应 n 棵子树
• 关键字个数的范围不同： B树： 根结点的关键字个数：1 \leq n \leq m - 1 非根内部结点的关键字个数：\lceil \frac{m}{2} \rceil -1 \leq n \leq m - 1 B+树 根叶结点的关键字个数：1 \leq n \leq m 非叶根结点的关键字个数：2 \leq n \leq m 非根内部结点的关键字个数：\lceil \frac{m}{2} \rceil \leq n \leq m
• 关键字的作用不同：
  • B树 中，每个结点中的关键字既充当子树的分界点，也直接关联或指向其对应的数据记录
  • B+树：
    • 叶结点 中的关键字包含了相应记录的存储地址
    • 非叶结点 中的关键字仅作为索引，且每个索引对应着一棵子树。我们无法通过这些索引找到相应记录的存储地址，只能够找到该索引对应的子树；
• 关键字的总数量不同：
  • B树 中，每个结点中的关键字均不相同
  • B+树 中，叶结点包含了全部的关键字，非叶结点中则会出现重复的关键字作为索引值；
• 树的形态不同：
  • B树 是一棵严格的 多路平衡查找树
  • B+树 则是一棵 多路平衡查找树 与一个 有序链表 的结合体，其 终端结点 既是 查找树 中的 叶子结点，也是 有序链表 中的 链表结点；
• 查找性能不同：
  • B树​ 的查询性能不稳定。最好情况是目标关键字在根节点，一次查找即命中；最坏情况则需要查找到叶子节点。此外，在进行范围查询时，效率较低。
  • B+树​ 的每一次查询都必须走一条从根结点到叶子结点的路径，因此查询速度非常稳定。同时，得益于叶子结点的顺序链表，其范围查询效率极高。

结语

通过对 B树 局限性的分析和对 B+树 深入探讨，我们现在可以清晰地看到这两种数据结构在设计哲学和实际效能上的根本差异。 B+树 作为 B树 的优化变体，通过几个关键改进解决了 B树 在数据库应用中面临的核心问题。 ✨ B+树的核心优势 B+树 最显著的特征是数据与索引的分离：所有数据记录都存储在叶子节点中，非叶子节点仅作为索引路径。这种设计带来了多方面的优势：

• 在查询性能上，B+树 提供了更加稳定的表现。由于每次查询都必须从根节点遍历到叶子节点，查询路径长度固定，使得查询效率具有可预测性。相比之下，B树 的查询性能波动较大，最好情况下可能在根节点就找到数据，最坏情况则需要访问到叶子节点。
• 对于范围查询，B+树的优势更为明显。叶子节点通过指针顺序连接形成的链表结构，使得范围查询只需找到起始点后顺链扫描即可，极大提升了效率。而 B树 进行范围查询时需要在不同层级的节点间来回跳跃，效率较低。
• 在空间利用率方面，B+树 的非叶子节点仅存储索引信息，相同大小的节点可以容纳更多的关键字，从而降低了树的高度，减少了磁盘I/O次数。

🔄 结构稳定性与适用场景 B+树的结构设计还带来了更好的稳定性。插入和删除操作主要集中在叶子节点进行，减少了节点分裂和合并的频率，维护了树的平衡性。这种特性使 B+树 特别适合需要频繁更新和查询的大型数据库系统。 从 教学视角 来看，B+树 “子树个数=关键字个数” 的特性使其概念更加清晰，易于理解其作为 多路分块查找树 的本质。虽然实际数据库实现多采用 算法视角，但 教学视角 为我们理解 B+树 的核心思想提供了直观的桥梁。 💎 总结 B+树通过数据与索引分离、叶子节点链表连接等创新设计，在 B树 的基础上实现了查询性能优化、空间利用率提升和结构稳定性增强，使其成为现代数据库系统的首选索引结构。理解 B+树 的工作原理，对于设计高效的数据存储和检索系统具有重要意义。 希望本篇博客能够帮助您建立对 B+树 的全面认识，为后续的数据库学习和应用开发打下坚实基础！

互动与分享

• 点赞👍 - 您的认可是我持续创作的最大动力
• 收藏⭐ - 方便随时回顾这些重要的基础概念
• 转发↗️ - 分享给更多可能需要的朋友
• 评论💬 - 欢迎留下您的宝贵意见或想讨论的话题

感谢您的耐心阅读！ 关注博主，不错过更多技术干货。我们下一篇再见！