GPU矩阵分块｜让大矩阵运算速度起飞

AI老马

发布于 2026-01-13 15:11:20

2130

文章被收录于专栏：AI前沿技术AI前沿技术

GPU的片上共享内存有限，完整的大矩阵的运算会导致内存溢出，对矩阵分块应用并行计算是必备的优化方法，那如何对矩阵分块，分块后如何并行计算？了解以上问题可以加深对涉及大量矩阵运算算法的理解。

1）如何对大矩阵进行分块，矩阵分块基于怎样的数学原理 2）分块后的矩阵如何利用多GPU核心进行并行计算，提高计算效率 3）Tile Size 分块大小如何选择，需要考虑哪些限制因素

1，矩阵分块（Tiling）原理

矩阵分块核心目标是：优化内存访问效率，避免片上内存溢出。

传统的矩阵乘法直接计算完整矩阵，若矩阵规模较大，会导致片上内存（如缓存、寄存器）无法容纳所有中间数据，进而频繁访问主存，计算效率降低。

1.1，为什么矩阵可以拆解为 Tile-wise 矩阵？

矩阵拆解的可行性基于以下两点：

• 加法结合律

矩阵乘法满足分配律与加法结合律，即对于矩阵 A,B,C 有：。扩展到分块场景，整个矩阵乘法可拆解为多个小块矩阵乘法的和。

例如，若将矩阵 A 和 B 划分为多个子矩阵（Tile），则：其中和为分块后的子矩阵，通过累加所有子矩阵的乘积，最终得到完整结果。

• 硬件内存限制的适配：

GPU 的 Shared Memory、CPU 缓存的片上内存容量远小于主存，分块后每次仅需在片上存储少量子矩阵，无论原矩阵规模多大，都能将内存占用控制在硬件限制内，避免溢出。

1.2，实例 4×4 矩阵分块乘法

以两个 4×4 矩阵 A 和 B 相乘为例，将其划分为 2×2 的子矩阵（T=2），分块计算过程。

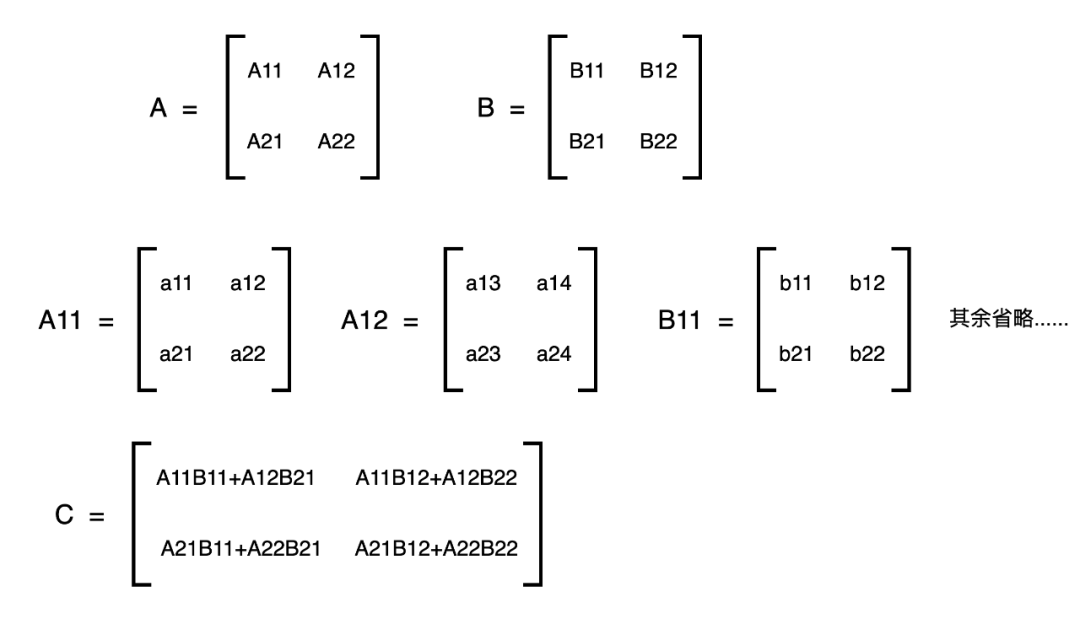
分块计算的执行流程（以 C11 为例）

• 将 A11 和 B11 加载到片上内存，计算 A11*B11，暂存结果 C11_temp。
• 卸载 B11，加载 A12和B21，计算 A12 * B21，并将结果累加到 C11_temp中，得到最终 C11。
• 重复上述过程计算其它子块，最终组合成完整矩阵 C。

分块计算的内存优势

• 传统计算的内存占用与元素大小正相关：直接计算 4×4 矩阵乘法需存储 4×4×2=32 个元素，若矩阵更大，内存占用线性增长。
• 分块计算与矩阵规模解耦：当T=2时，每次仅需在片上存储 3 个 2×2 子矩阵（如 A11, B11,和 A11*B11 的中间结果），共 3×2×2=12 个元素，远小于传统方式。即使矩阵扩展到 1024×1024，分块后片上内存仍仅需个元素（如 T=32 时，为 3×32×32=3072 个元素），与矩阵规模解耦。

矩阵分块代码：

def tile_matrix(matrix, tile_size):
    """将矩阵分割为多个tile"""
    rows, cols = matrix.shape
    tiles = []
    
    for i inrange(0, rows, tile_size):
        row_tiles = []
        for j inrange(0, cols, tile_size):
            # 提取一个tile
            tile = matrix[i:i+tile_size, j:j+tile_size]
            row_tiles.append(tile)
        tiles.append(row_tiles)
    
    return tiles

分块计算代码：

def matrix_multiply_tiled(A, B, tile_size):
    """使用分块技术实现矩阵乘法"""
    ...
    # 遍历所有tile组合进行计算
    for i inrange(num_tile_rows):
        for j inrange(num_tile_cols):
            # 初始化当前C的tile为零矩阵
            current_C_tile = np.zeros_like(C_tiles[i][j])
            
            # 累加所有k对应的乘积
            for k inrange(num_tile_k):
                A_tile = A_tiles[i][k]
                B_tile = B_tiles[k][j]
                # 计算两个tile的乘积并累加到结果
                current_C_tile += A_tile @ B_tile
            
            # 将计算结果写回C的对应tile位置
            tile_row_start = i * tile_size
            tile_col_start = j * tile_size
            C[tile_row_start:tile_row_start+current_C_tile.shape[0], 
              tile_col_start:tile_col_start+current_C_tile.shape[1]] = current_C_tile
    
    return C

通过分块，矩阵运算得以在硬件约束下高效执行，这也是现代高性能计算框架（如 CUDA、OpenBLAS）的核心优化手段之一。熟悉了矩阵分块的基本原理，再来看下不同分块是怎样并行计算，加速整个矩阵计算过程的。

2，GPU 分块矩阵乘法的并行计算

在 GPU 上实现分块矩阵乘法时，主要利用 CUDA 的线程层次结构（Thread Hierarchy）将计算任务分配给大量 CUDA 核心，并通过共享内存（Shared Memory）优化数据访问效率。

2.1，CUDA 线程层次结构与矩阵分块的映射

CUDA 将线程组织为线程块（Thread Block）和网格（Grid）：

• 线程块：由多个线程组成，共享片上内存（Shared Memory），线程间可协作计算。
• 网格：由多个线程块组成，分布在不同的 SM（Streaming Multiprocessor）上并行执行。

对于分块矩阵乘法，典型的映射策略是：

• 每个线程块计算一个结果子矩阵（Tile）
• 每个线程计算结果 Tile 中的一个元素

2.2， 4×4 矩阵在 GPU 上的分块并行计算

以两个 4×4 矩阵相乘为例，假设使用 2×2 的分块大小（T=2），并映射到 GPU 线程。

1，矩阵分块

• 每个 Tile 的大小为 2×2。
• 每个线程块负责计算一个 C 的 Tile。
• 每个线程块包含 2×2=4 个线程，每个线程计算 C 中一个元素，如上图一中的C矩阵所示。

2，加载数据到共享内存：

• 线程块内所有线程协作，将 A11 和 B11 从全局内存加载到共享内存。
• 然后所有线程从共享内存读取数据进行计算，避免重复访问全局内存。

3，线程并行计算：

每个线程计算 C11 中的一个元素，例如：

• 线程 T(0,0) 计算 C11 [0,0] = A11 [0,0]*B11 [0,0] + A11 [0,1]*B11 [1,0]
• 线程 T(0,1) 计算 C11 [0,1] = A11 [0,0]*B11 [0,1] + A11 [0,1]*B11 [1,1]
• 依此类推...

4，结果写回全局内存：

计算完成后，将 C11 写回全局内存。同理对于C12，C21，C22也是同样的计算过程。

2.3 多线程块并行计算

整个网格包含 4 个线程块，并行计算 C 的 4 个 Tile：

• 线程块 TB(0,0) 计算 C11
• 线程块 TB(0,1) 计算 C12
• 线程块 TB(1,0) 计算 C21
• 线程块 TB(1,1) 计算 C22

这些线程块可在不同的 SM 上并行执行，大幅加速计算。

总结： GPU 上分块矩阵乘法通过以下方式实现高效并行计算：

• 分块策略：将大矩阵分解为小 Tile，控制内存访问
• 线程映射：每个线程块计算一个 Tile，每个线程计算一个元素
• 共享内存优化：利用快速的共享内存减少全局内存访问
• 大规模并行：利用数千个 CUDA 核心同时计算不同 Tile

3，如何选择合适的Tile Size？

分块大小（Tile Size）的选择，直接影响性能，太小增加内存访问次数，降低计算效率。太大可能导致共享内存溢出，或无法充分利用线程并行性。典型的 Tile Size 选择为 16×16 或 32×32，具体取决于 GPU 架构和矩阵规模。具体Tile Size 的选择考虑以下几个方面的限制

3.1，共享内存大小

• 限制：每个 SM（Streaming Multiprocessor）的共享内存容量有限（如 NVIDIA V100 为 96KB，RTX 3080 为 64KB）

• 影响：合适的Tile Size 需保证， A 和 B 的分片后的 Tile 能同时放入共享内存

• 计算公式

每个线程块所需共享内存 = 2 × Tile Size² × sizeof(float)

例如：Tile Size=32 时需 2×32×32×4B = 8KB（远小于 64KB，可行），若 Tile Size=64，则需 32KB（接近某些 GPU 限制，需谨慎）

3.2，线程块大小限制

• 限制：每个线程块的最大线程数通常为 1024
• 影响：Tile Size² ≤ 1024，即 Tile Size ≤ 32
• 典型配置16×16 = 256 线程（安全选择）32×32 = 1024 线程（最大利用）

3.3，矩阵维度与 Tile Size 的整除性

• 要求：矩阵维度需能被 Tile Size 整除，避免边界处理复杂度示例，矩阵 A 为 1024×1024，Tile Size 可选 16、32、64（均能整除 1024）。若矩阵 A 为 1000×1000，Tile Size 选 16（1000÷16=62.5，需补零至 1008）需要注意大矩阵和小Tile 的平衡，当大矩阵时，使用较大 Tile Size（如 32）减少分块数，降低调度开销。小矩阵时，使用较小 Tile Size（如 16）避免共享内存浪费。

4，总结

分块技术的核心价值为：

• 内存优化：通过分块将大规模矩阵运算拆解为小尺度计算，确保片上内存占用恒定，适配硬件限制。
• 计算效率提升：减少主存访问次数，利用片上高速内存加速计算，尤其在 GPU 等异构计算设备中效果显著。
• 算法通用性：基于加法结合律的数学性质，分块技术可推广到矩阵求逆、LU 分解等多种数值计算场景。

如果使用pytorch框架进行训练或是推理，Tile size 会自动的进行调整，当手撸自定义算子时候，可能需要自己定义，对于大多数 GPU，32×32 是平衡内存和计算的良好起点。当共享内存有限或矩阵较小时，尝试 16×16 的分片。

以上主要是为大型矩阵是如何在GPU上进行分块计算，可以帮助理解模型前向和后向传播的过程，以及一些attention的优化方案。