数据结构（C语言篇）：（十七）选择排序

前言

排序算法是计算机科学中的基础课题，对数据处理效率有着决定性影响。在众多排序方法中，选择排序以其简洁性和直观性成为初学者理解算法设计的经典范例。该算法通过反复寻找未排序部分的最小元素并交换位置来完成排序，体现了分治思想的核心逻辑。尽管时间复杂度为O(n²)使其不适用于大规模数据集，但选择排序在算法教学中具有不可替代的价值，能够清晰展示基本排序原理和循环控制结构。本文将深入解析选择排序的实现机制、性能特征以及优化方向，为读者构建系统的算法认知框架提供技术参考。

一、直接选择排序

1.1 选择排序的基本思想

选择排序（Selection Sort）是一种简单直观的排序算法，它的基本思想可概括为：每一趟从待排序的元素中选出值最小（或最大）的元素，将其与待排序部分的起始位置元素交换，直至整个序列有序。它的核心是 “选最小（大），放前面”，通过逐步缩小待排序范围，最终完成整个数组的排序。

选择排序其实也可以分为很多种，在本期博客中，我们将来学习其中的直接选择排序和堆排序。

1.2 直接选择排序的思路

1. 在元素集合 array[i]--array[n-1] 中选择关键码最大（小）的数据元素；

2. 若它不是这组元素中的最后一个（第一个）元素，则将它与这组元素中的最后一个（第一个）元素交换；

3. 在剩余的 array[i]--array[n-2]（array[i+1]-array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素。

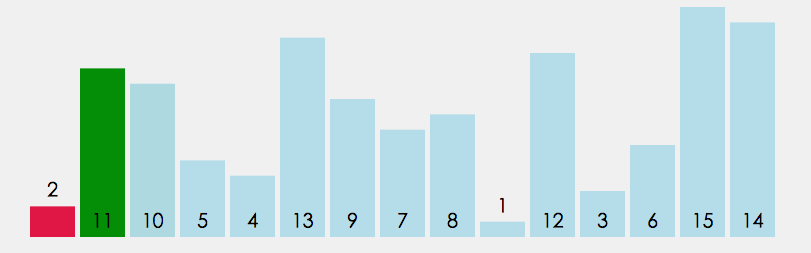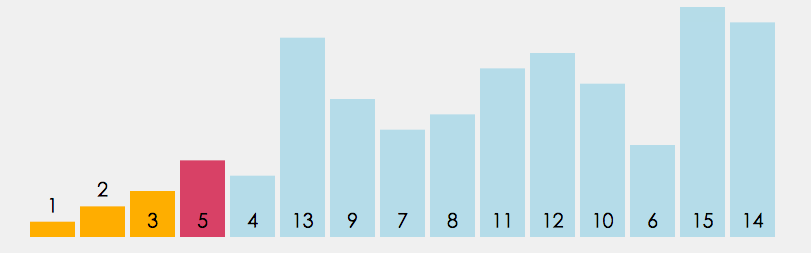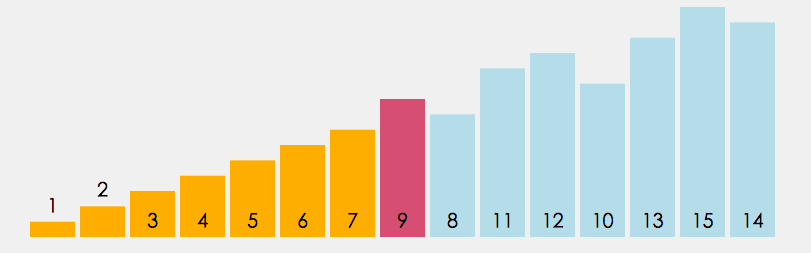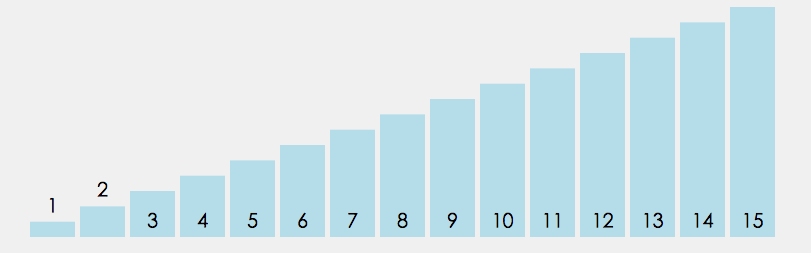
代码实现：

void SelectSort(int* a, int n)
{
    int begin = 0, end = n - 1;
    while (begin < end)
    {
        int mini = begin, maxi = begin;
        for (int i = begin; i <= end; i++)
        {
            if (a[i] > a[maxi])
            {
                maxi = i;
            } 
            if (a[i] < a[mini])
            {
                mini = i;
            }
        } 
        if (begin == maxi)
        {
            maxi = mini;
        } 
        swap(&a[mini], &a[begin]);
        swap(&a[maxi], &a[end]);

        ++begin;
        --end;
    }
}

1.3 直接选择排序的特性

（1）操作方式：通过 "选择最小值 + 交换位置" 实现排序，无需额外辅助空间（原地排序）。

（2）稳定性：不稳定排序。例如对 [3, 2, 3, 1] 排序时，第一个 3 会与 1 交换，导致两个 3 的相对位置改变。

（3）适用数据：适用于数组、列表等随机访问结构，对链表效率较低（因查找最小值需频繁遍历）。

（4）优缺点：

（5）时间复杂度计算：

这里我们以升序排序为例，直接选择排序的核心操作是 "比较" 和 "交换"，其中比较操作是主导因素：

1. 外层循环：共执行 n-1 趟（需确定前 n-1 个元素的位置，最后一个元素自然有序）。
2. 内层循环：每趟在待排序区间 [i, n-1] 中查找最小值，比较次数随趟数减少：
   • 第 1 趟：比较 n-1 次（i=0，j 从 1 到 n-1）
   • 第 2 趟：比较 n-2 次（i=1，j 从 2 到 n-1）
   • ...
   • 第 n-1 趟：比较 1 次（i=n-2，j=n-1）
3. 总比较次数： 求和公式为 (n-1) + (n-2) + ... + 1 = n(n-1)/2，这是一个关于 n 的二次函数。
4. 时间复杂度： 忽略常数系数（1/2）和低阶项（-n），最终时间复杂度为 O(n²)，且最好、最坏、平均情况均为 O (n²)（因比较次数固定）。

二、堆排序

在之前介绍堆的相关应用的博客中，我为大家介绍了堆排序这一排序方法。堆排序（Heapsort）这种排序方法实际上是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它的核心思想是利用堆的特性（大顶堆或小顶堆），通过反复提取堆顶元素并调整堆结构，实现整个序列的排序。这里我就再帮大家复习一下堆排序：

堆排序的核心步骤可概括为：

1. 构建初始堆：将待排序数组转换为一个大顶堆（或小顶堆，取决于排序方向）。大顶堆的特性是：每个父节点的值大于或等于其左右子节点的值。
2. 提取堆顶元素：将堆顶元素（最大值）与堆的最后一个元素交换，此时最大值被放置到数组末尾（即其最终位置）。
3. 调整堆结构：交换后，堆的规模减小 1（排除已排序的末尾元素），需要对剩余元素重新调整为大顶堆。
4. 重复操作：重复步骤 2 和 3，直到堆的规模为 1，此时整个数组排序完成。

完整代码如下：

#include <stdio.h>

// 交换两个元素的值
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 堆调整函数：将以i为根的子树调整为大顶堆
// n为堆的大小，i为需要调整的节点索引
void heapify(int arr[], int n, int i) {
    int largest = i;        // 初始化最大值为根节点
    int left = 2 * i + 1;   // 左子节点索引 = 2*i + 1
    int right = 2 * i + 2;  // 右子节点索引 = 2*i + 2

    // 如果左子节点大于根节点
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // 如果右子节点大于当前最大值
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 如果最大值不是根节点
    if (largest != i) {
        swap(&arr[i], &arr[largest]);
        
        // 递归调整受影响的子树
        heapify(arr, n, largest);
    }
}

// 堆排序主函数
void heapSort(int arr[], int n) {
    // 构建大顶堆
    // 从最后一个非叶子节点开始向上调整
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    // 逐个提取堆顶元素（最大值）
    for (int i = n - 1; i > 0; i--) {
        // 将当前堆顶（最大值）与堆的最后一个元素交换
        swap(&arr[0], &arr[i]);
        
        // 对剩余元素重新调整为大顶堆
        heapify(arr, i, 0);
    }
}

假设待排序数组为 [4, 10, 3, 5, 1]， 堆排序的执行流程如下（以大顶堆升序排序为例）：

1.构建初始大顶堆：

将数组视为完全二叉树，从最后一个非叶子节点（索引 1，值为 10）开始调整，最终得到大顶堆 [10, 5, 3, 4, 1]。

2.第一趟排序：

交换堆顶（10）与末尾元素（1）→ 数组变为 [1, 5, 3, 4, 10]（10 已确定为最大值）；

对前 4 个元素 [1, 5, 3, 4] 重新调整为大顶堆 → [5, 4, 3, 1]，数组整体为 [5, 4, 3, 1, 10]。

3.第二趟排序：

交换堆顶（5）与当前末尾元素（1）→ 数组变为 [1, 4, 3, 5, 10]（5 已确定位置）；

对前 3 个元素 [1, 4, 3] 调整为大顶堆 → [4, 1, 3]，数组整体为 [4, 1, 3, 5, 10]。

4.第三趟排序：

交换堆顶（4）与当前末尾元素（3）→ 数组变为 [3, 1, 4, 5, 10]（4 已确定位置）；

对前 2 个元素 [3, 1] 调整为大顶堆 → [3, 1]，数组整体为 [3, 1, 4, 5, 10]。

5.第四趟排序：

交换堆顶（3）与当前末尾元素（1）→ 数组变为 [1, 3, 4, 5, 10]（3 已确定位置）；

剩余 1 个元素，排序完成，最终结果为 [1, 3, 4, 5, 10]。

堆排序的核心特点

• 时间复杂度：构建堆的时间为 O (n)，每次调整堆的时间为 O (log n)，共需调整 n-1 次，因此总时间复杂度为 O(n log n)（最好、最坏、平均情况均为此值）。
• 空间复杂度：仅需常数个临时变量，属于原地排序，空间复杂度为 O(1)。
• 稳定性：不稳定（交换堆顶元素时可能改变相等元素的相对位置）。
• 适用场景：适合大规模数据排序，对时间效率要求高但对稳定性无要求的场景。

综合上述可知，堆排序的优势在于时间复杂度稳定（不受数据分布影响），且空间效率高，是一种高性能的排序算法。

总结

本期博客我为大家介绍了两种选择排序算法 —— 直接选择排序和堆排序。希望大家再看完本期博客之后能加深对选择排序的认识，下期博客我们将继续学习排序算法中的交换排序，请大家多多支持！