《自动控制原理》- 第八章非线性控制系统分析

啊阿狸不会拉杆

发布于 2026-01-21 11:43:48

1110

8-1 非线性控制系统概述

非线性系统的基本概念

非线性控制系统是指系统中至少包含一个非线性元件或环节的控制系统。与线性系统相比，非线性系统具有许多独特的性质，如：

不满足叠加原理
可能存在极限环
对初始条件敏感
可能出现混沌现象

非线性系统与线性系统的区别

线性系统可以用线性微分方程描述，而非线性系统需要用非线性微分方程描述。线性系统的响应特性主要由系统参数决定，而非线性系统的响应还与输入信号的大小和形式有关。

下面是一个简单的非线性系统示例代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义非线性系统的微分方程：dx/dt = -x + x^3
def nonlinear_system(t, x):
    dx_dt = -x + x**3
    return dx_dt

# 定义线性系统的微分方程：dx/dt = -x
def linear_system(t, x):
    dx_dt = -x
    return dx_dt

# 求解微分方程
t_span = (0, 10)
t_eval = np.linspace(0, 10, 1000)

# 初始条件
x0 = [0.1, 1.0]  # 不同的初始条件

# 绘制结果
plt.figure(figsize=(12, 5))

# 非线性系统响应
plt.subplot(1, 2, 1)
for x0_val in x0:
    sol = solve_ivp(nonlinear_system, t_span, [x0_val], t_eval=t_eval, method='RK45')
    plt.plot(sol.t, sol.y[0], label=f'初始条件 x(0) = {x0_val}')
plt.title('非线性系统响应')
plt.xlabel('时间 t')
plt.ylabel('状态 x')
plt.legend()
plt.grid(True)

# 线性系统响应
plt.subplot(1, 2, 2)
for x0_val in x0:
    sol = solve_ivp(linear_system, t_span, [x0_val], t_eval=t_eval, method='RK45')
    plt.plot(sol.t, sol.y[0], label=f'初始条件 x(0) = {x0_val}')
plt.title('线性系统响应')
plt.xlabel('时间 t')
plt.ylabel('状态 x')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()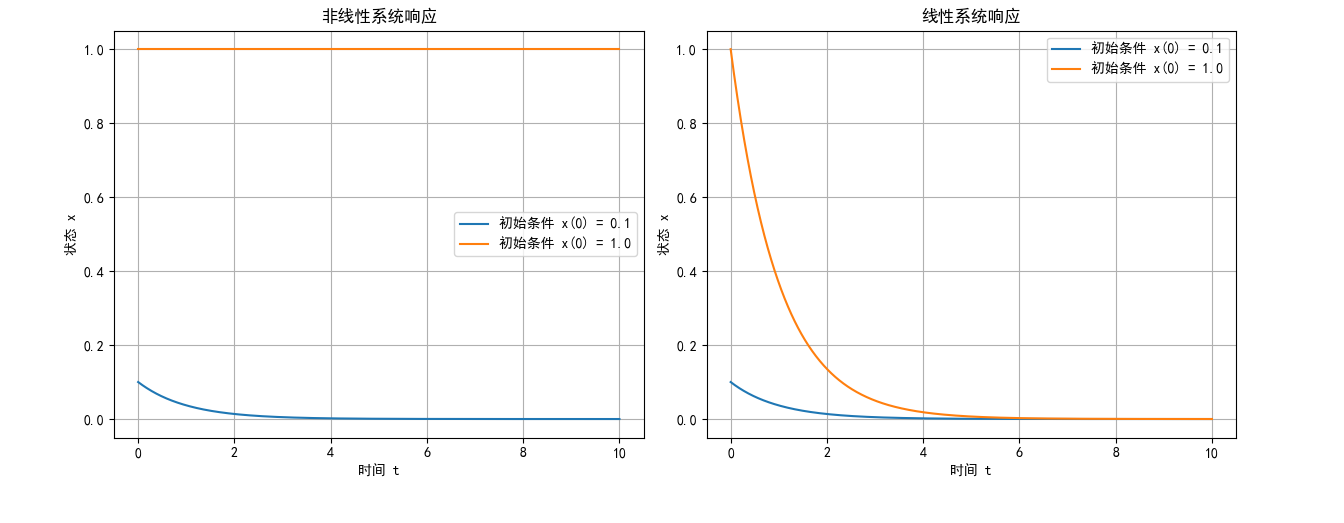

图 1：线性与非线性系统响应对比

非线性系统分析方法概述

非线性系统的分析方法主要包括：

相平面法（适用于一阶和二阶系统）
描述函数法（频域分析方法）
逆系统方法
李雅普诺夫稳定性分析
数值仿真方法

下面是一个非线性系统分析方法的思维导图：

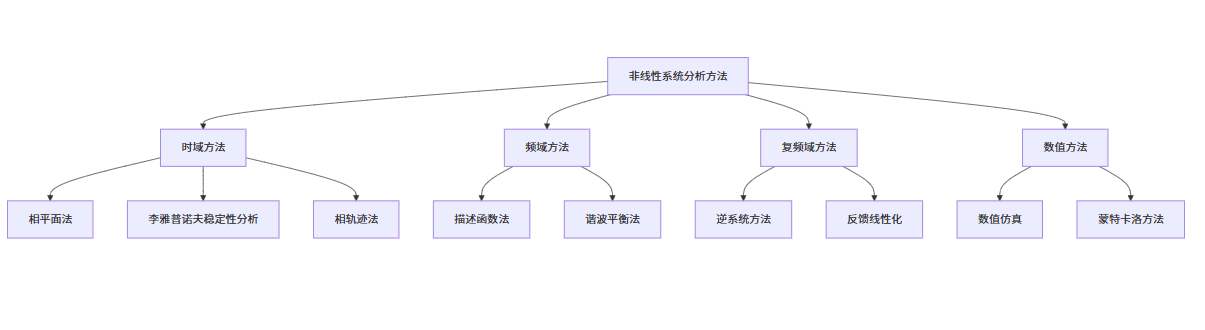
图 2：非线性系统分析方法思维导图

8-2 常见非线性特性及其对系统运动的影响

常见非线性特性

常见的非线性特性包括：

饱和特性
死区特性
间隙特性
继电特性
非线性增益特性
库仑摩擦特性

非线性特性对系统的影响

非线性特性会使系统产生不同于线性系统的响应特性，主要影响包括：

产生极限环振荡
改变系统的稳定性
引起系统的自激振荡
导致系统响应的畸变
影响系统的稳态误差

下面是一个包含饱和非线性特性的系统仿真代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义包含饱和非线性的系统微分方程
def saturated_system(t, x, u):
    # 饱和非线性函数
    def saturation(y, limit=1.0):
        return np.clip(y, -limit, limit)

    # 系统动态方程: dx/dt = -x + u(t)
    dx_dt = -x + saturation(u(t))
    return dx_dt


# 输入信号
def input_signal(t):
    return 2.0 * np.sin(t)  # 幅值为2的正弦输入


# 求解微分方程
t_span = (0, 20)
t_eval = np.linspace(0, 20, 1000)
x0 = [0.0]  # 初始条件

sol = solve_ivp(lambda t, x: saturated_system(t, x, input_signal),
                t_span, x0, t_eval=t_eval, method='RK45')

# 绘制结果
plt.figure(figsize=(12, 6))

plt.subplot(2, 1, 1)
plt.plot(sol.t, sol.y[0], 'b-', linewidth=2)
plt.title('包含饱和非线性的系统响应')
plt.xlabel('时间 t')
plt.ylabel('状态 x')
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(sol.t, [input_signal(t) for t in sol.t], 'r-', linewidth=2)
plt.plot(sol.t, [np.clip(input_signal(t), -1.0, 1.0) for t in sol.t], 'g--', linewidth=2)
plt.title('输入信号与饱和非线性输出')
plt.xlabel('时间 t')
plt.ylabel('信号幅值')
plt.legend(['输入信号', '饱和输出'])
plt.grid(True)

plt.tight_layout()
plt.show()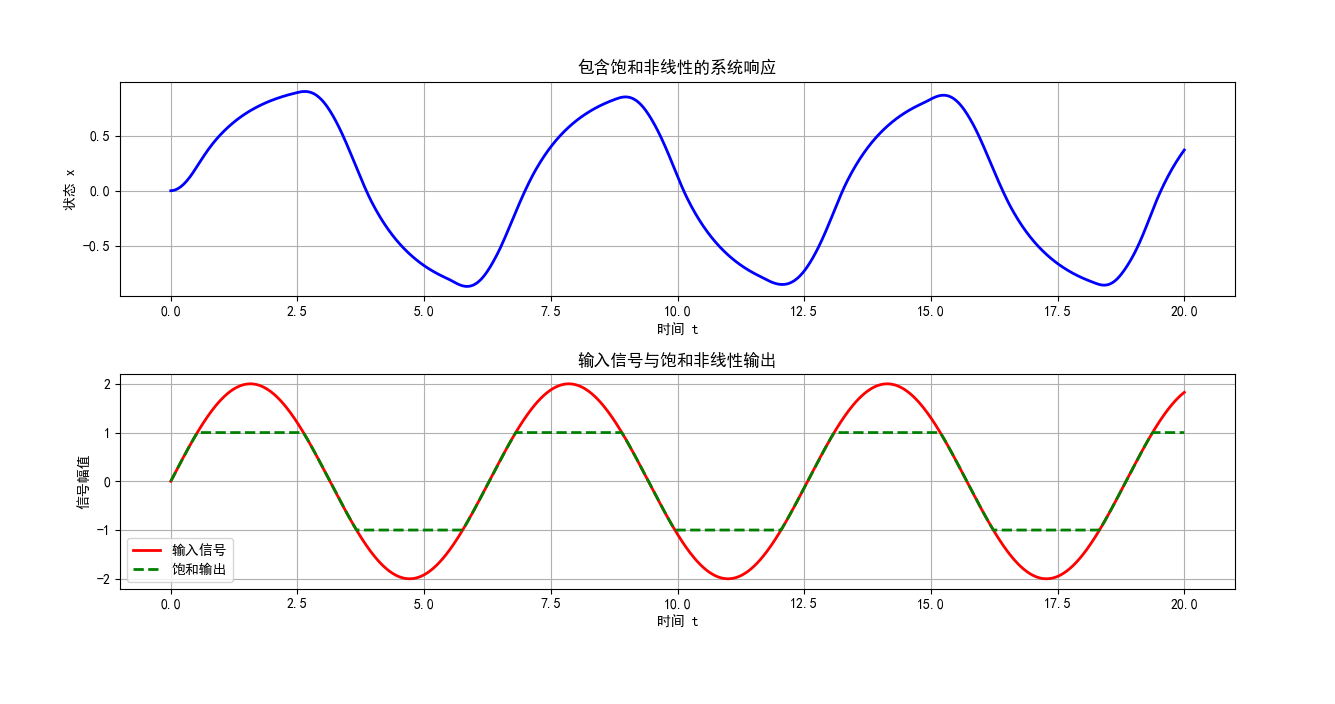

图 3：包含饱和非线性的系统响应

非线性特性综合案例

下面我们将模拟一个同时包含死区和间隙非线性特性的系统，并分析其响应特性：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义死区非线性特性
def dead_zone(y, dead_zone=0.5):
    if y > dead_zone:
        return y - dead_zone
    elif y < -dead_zone:
        return y + dead_zone
    else:
        return 0.0


# 定义间隙非线性特性
class Hysteresis:
    def __init__(self, width=1.0, dead_zone=0.2):
        self.width = width
        self.dead_zone = dead_zone
        self.prev_output = 0.0
        self.switch_point = 0.0

    def update(self, y):
        if y >= self.switch_point + self.dead_zone:
            self.prev_output = y - self.width
            self.switch_point = y
        elif y <= self.switch_point - self.dead_zone:
            self.prev_output = y + self.width
            self.switch_point = y
        return self.prev_output


# 定义包含死区和间隙非线性的系统
def nonlinear_system(t, x, u, hysteresis):
    # 应用死区非线性
    dead_zone_output = dead_zone(u(t))
    # 应用间隙非线性
    hysteresis_output = hysteresis.update(dead_zone_output)
    # 系统动态方程: dx/dt = -x + 非线性输出
    dx_dt = -x + hysteresis_output
    return dx_dt


# 输入信号
def input_signal(t):
    return 3.0 * np.sin(t)  # 幅值为3的正弦输入


# 求解微分方程
t_span = (0, 20)
t_eval = np.linspace(0, 20, 1000)
x0 = [0.0]  # 初始条件
hysteresis = Hysteresis()

# 存储中间结果用于绘图
x_vals = []
dead_zone_vals = []
hysteresis_vals = []
u_vals = []

# 求解微分方程
sol = solve_ivp(lambda t, x: nonlinear_system(t, x, input_signal, hysteresis),
                t_span, x0, t_eval=t_eval, method='RK45')

# 存储中间结果
for t, x in zip(sol.t, sol.y.T):
    u = input_signal(t)
    dead_zone_output = dead_zone(u)
    hysteresis_output = hysteresis.update(dead_zone_output)
    x_vals.append(x[0])
    dead_zone_vals.append(dead_zone_output)
    hysteresis_vals.append(hysteresis_output)
    u_vals.append(u)

# 转换为numpy数组以便绘图
x_vals = np.array(x_vals)
dead_zone_vals = np.array(dead_zone_vals)
hysteresis_vals = np.array(hysteresis_vals)
u_vals = np.array(u_vals)

# 绘制结果
plt.figure(figsize=(15, 8))

plt.subplot(3, 1, 1)
plt.plot(t_eval, u_vals, 'r-', linewidth=2)
plt.title('输入信号')
plt.xlabel('时间 t')
plt.ylabel('幅值')
plt.grid(True)

plt.subplot(3, 1, 2)
plt.plot(t_eval, dead_zone_vals, 'g-', linewidth=2)
plt.title('死区非线性输出')
plt.xlabel('时间 t')
plt.ylabel('幅值')
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(t_eval, x_vals, 'b-', linewidth=2)
plt.title('包含死区和间隙非线性的系统响应')
plt.xlabel('时间 t')
plt.ylabel('状态 x')
plt.grid(True)

plt.tight_layout()
plt.show()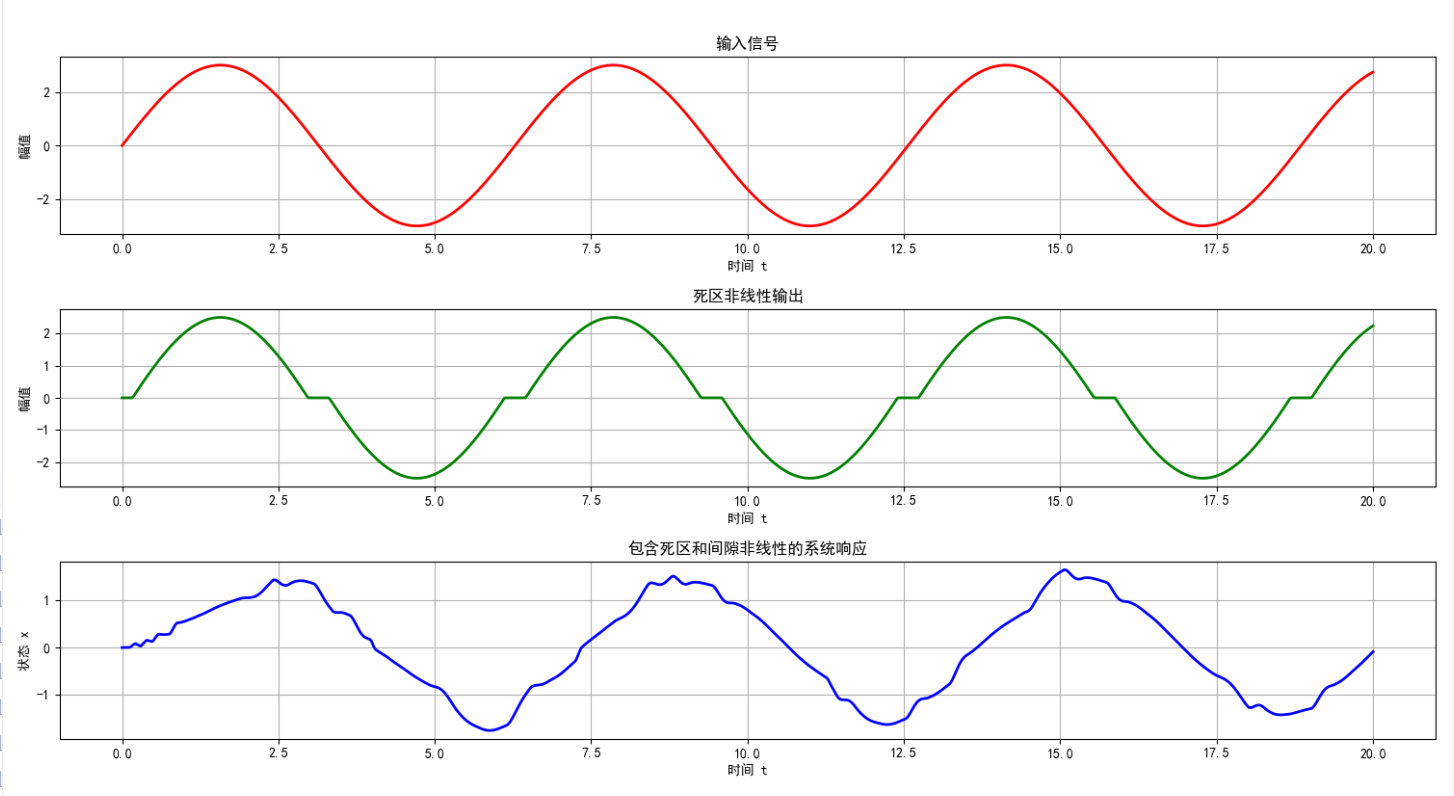

图 4：包含死区和间隙非线性的系统响应

8-3 相平面法

相平面法基本概念

相平面法是分析一、二阶非线性系统的有效方法。对于二阶系统，其状态可以用两个变量表示，这两个变量构成的平面称为相平面。系统的运动轨迹在相平面上的曲线称为相轨迹。

相平面法的基本原理

对于二阶系统：

dx1/dt = f1(x1, x2)
dx2/dt = f2(x1, x2)

相轨迹的斜率为：

dx2/dx1 = f2(x1, x2)/f1(x1, x2)

下面是一个使用相平面法分析非线性系统的代码示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义非线性系统的微分方程
def nonlinear_system(t, x):
    # 非线性阻尼项：dx1/dt = x2
    # 非线性恢复力：dx2/dt = -x1 - 0.2*x2 + 0.1*x2^3
    dx1_dt = x[1]
    dx2_dt = -x[0] - 0.2 * x[1] + 0.1 * x[1]**3
    return [dx1_dt, dx2_dt]

# 初始条件
x0_values = [
    [0.1, 0.0],
    [1.0, 0.0],
    [2.0, 0.0],
    [3.0, 0.0]
]

# 时间范围
t_span = (0, 50)
t_eval = np.linspace(0, 50, 1000)

# 绘制相平面图
plt.figure(figsize=(10, 8))

for x0 in x0_values:
    sol = solve_ivp(nonlinear_system, t_span, x0, t_eval=t_eval, method='RK45')
    plt.plot(sol.y[0], sol.y[1], label=f'初始条件: x1(0)={x0[0]}, x2(0)={x0[1]}')

# 绘制坐标轴和网格
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('非线性系统的相平面图')
plt.grid(True)
plt.legend()
plt.axis('equal')
plt.xlim(-4, 4)
plt.ylim(-4, 4)

# 绘制原点
plt.plot(0, 0, 'ro', markersize=8)
plt.text(0.1, 0.1, '原点', fontsize=12)

plt.tight_layout()
plt.show()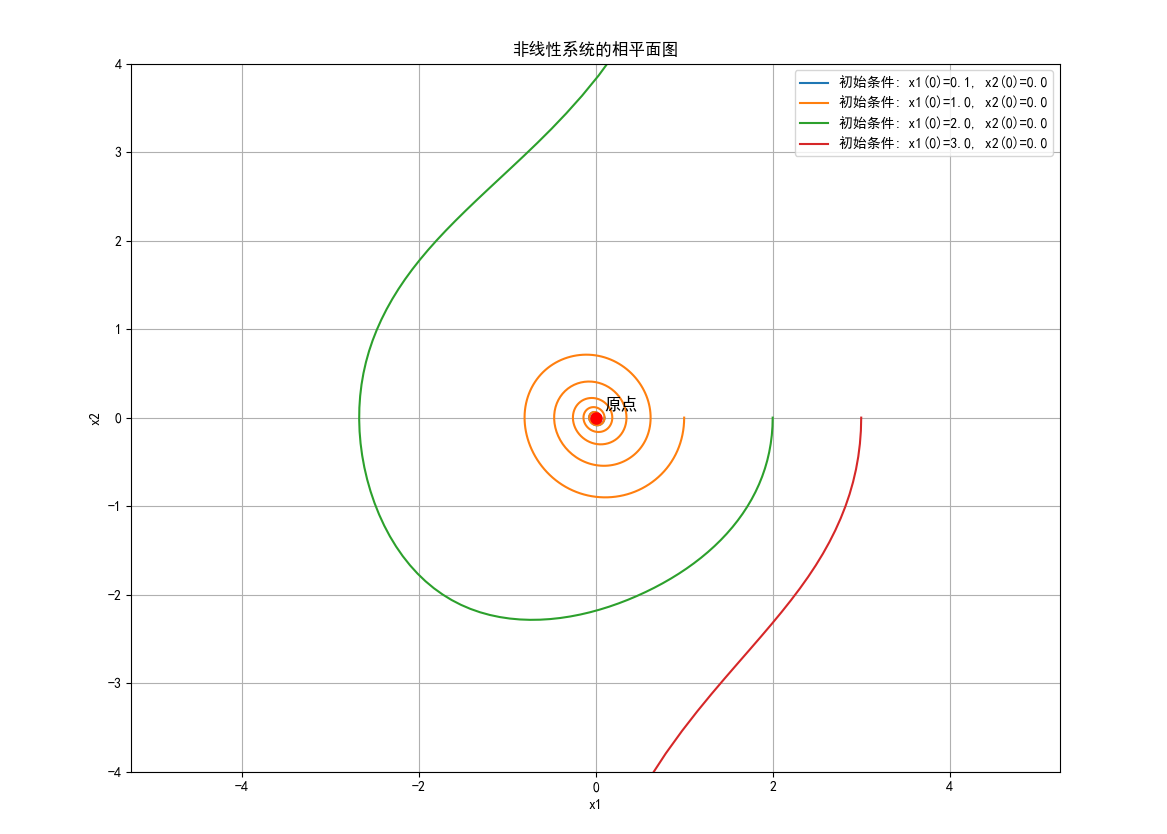

图 5：非线性系统的相平面图

极限环分析

极限环是相平面上的封闭轨迹，表示系统的持续振荡。下面我们分析一个能产生极限环的范德波尔 (Van der Pol) 振荡器：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 范德波尔振荡器参数
mu = 1.0  # 非线性阻尼系数

# 定义范德波尔振荡器的微分方程
def vanderpol_oscillator(t, x):
    # dx1/dt = x2
    # dx2/dt = mu*(1 - x1^2)*x2 - x1
    dx1_dt = x[1]
    dx2_dt = mu * (1 - x[0]**2) * x[1] - x[0]
    return [dx1_dt, dx2_dt]

# 初始条件
x0 = [0.1, 0.0]  # 接近原点的初始条件

# 时间范围
t_span = (0, 100)
t_eval = np.linspace(0, 100, 10000)

# 求解微分方程
sol = solve_ivp(vanderpol_oscillator, t_span, x0, t_eval=t_eval, method='RK45')

# 绘制相平面图和时间响应
plt.figure(figsize=(12, 5))

# 相平面图
plt.subplot(1, 2, 1)
plt.plot(sol.y[0], sol.y[1], 'b-', linewidth=1.5)
plt.title(f'范德波尔振荡器相平面图 (μ = {mu})')
plt.xlabel('x1')
plt.ylabel('x2')
plt.grid(True)
plt.axis('equal')

# 时间响应
plt.subplot(1, 2, 2)
plt.plot(sol.t, sol.y[0], 'r-', linewidth=1.5)
plt.title(f'范德波尔振荡器时间响应 (μ = {mu})')
plt.xlabel('时间 t')
plt.ylabel('x1')
plt.grid(True)

plt.tight_layout()
plt.show()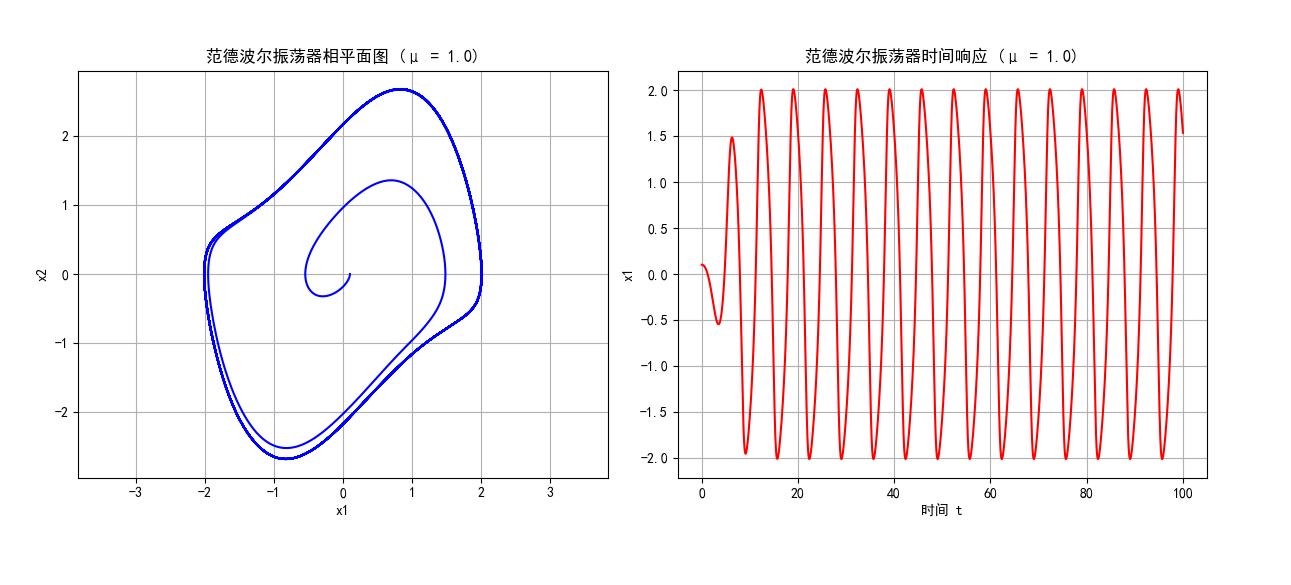

图 6：范德波尔振荡器的相平面图和时间响应

8-4 描述函数法

描述函数法基本概念

描述函数法是一种频域分析方法，用于分析非线性系统的稳定性和极限环特性。它将非线性环节用一个复数函数来表示，该函数描述了非线性环节在正弦输入下的基波输出与输入的复数比。

描述函数的定义

对于非线性环节，输入为 x (t) = Xsin (ωt)，输出为 y (t)，则描述函数 N (X) 定义为：

N(X) = Y1/X ∠φ1

其中 Y1 是输出 y (t) 的基波分量幅值，φ1 是基波分量与输入的相位差。

下面是一个计算常见非线性特性描述函数的代码：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 饱和非线性的描述函数
def saturation_describing_function(X, a=1.0, k=1.0):
    """
    计算饱和非线性的描述函数

    参数:
    X -- 输入信号幅值
    a -- 饱和阈值
    k -- 线性增益

    返回:
    N -- 描述函数(复数形式)
    """
    if X <= a:
        return complex(k, 0)
    else:
        term1 = (2 * k / np.pi) * np.arcsin(a / X)
        term2 = (2 * k / np.pi) * (a / X) * np.sqrt(1 - (a / X) ** 2)
        return complex(term1 + term2, 0)


# 死区非线性的描述函数
def dead_zone_describing_function(X, a=1.0, k=1.0):
    """
    计算死区非线性的描述函数

    参数:
    X -- 输入信号幅值
    a -- 死区阈值
    k -- 线性增益

    返回:
    N -- 描述函数(复数形式)
    """
    if X <= a:
        return complex(0, 0)
    else:
        term1 = (2 * k / np.pi) * np.arcsin(a / X)
        term2 = (2 * k / np.pi) * (a / X) * np.sqrt(1 - (a / X) ** 2)
        return complex(k - term1 - term2, 0)


# 继电非线性的描述函数
def relay_describing_function(X, M=1.0):
    """
    计算继电非线性的描述函数

    参数:
    X -- 输入信号幅值
    M -- 继电输出幅值

    返回:
    N -- 描述函数(复数形式)
    """
    return complex(4 * M / (np.pi * X), 0)


# 绘制描述函数曲线
X_vals = np.linspace(0.1, 5, 100)

# 饱和非线性
saturation_N = [saturation_describing_function(X, a=1.0, k=1.0) for X in X_vals]
saturation_abs = [np.abs(N) for N in saturation_N]

# 死区非线性
dead_zone_N = [dead_zone_describing_function(X, a=1.0, k=1.0) for X in X_vals]
dead_zone_abs = [np.abs(N) for N in dead_zone_N]

# 继电非线性
relay_N = [relay_describing_function(X, M=1.0) for X in X_vals]
relay_abs = [np.abs(N) for N in relay_N]

# 绘制幅值曲线
plt.figure(figsize=(10, 6))
plt.plot(X_vals, saturation_abs, 'b-', label='饱和非线性')
plt.plot(X_vals, dead_zone_abs, 'g-', label='死区非线性')
plt.plot(X_vals, relay_abs, 'r-', label='继电非线性')
plt.title('常见非线性特性的描述函数幅值')
plt.xlabel('输入信号幅值 X')
plt.ylabel('描述函数幅值 |N(X)|')
plt.grid(True)
plt.legend()
plt.xlim(0, 5)
plt.ylim(0, 1.5)

plt.tight_layout()
plt.show()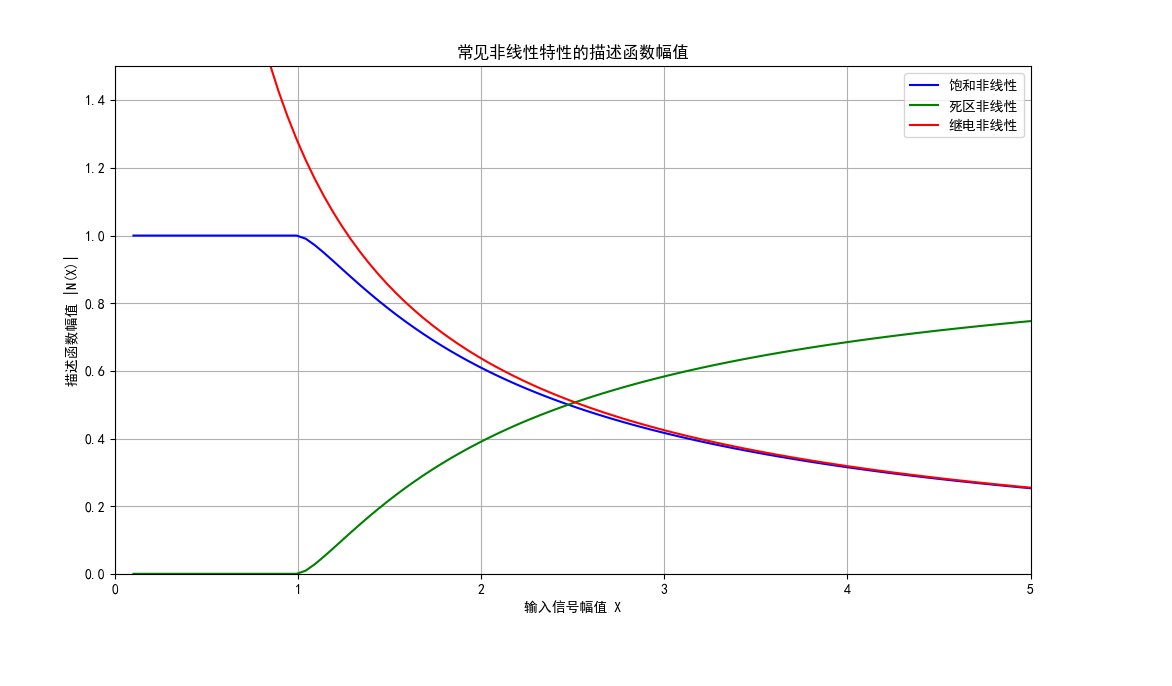

图 7：常见非线性特性的描述函数幅值曲线

描述函数法分析极限环

描述函数法可以用来分析非线性系统是否存在极限环。考虑一个非线性系统，由线性部分 G (jω) 和非线性部分 N (X) 组成，闭环系统的特征方程为：

1 + N(X)G(jω) = 0

即：

G(jω) = -1/N(X)

当线性部分的频率特性 G (jω) 与 - 1/N (X) 曲线相交时，可能存在极限环。

下面是一个使用描述函数法分析极限环的示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义线性系统传递函数
# G(s) = 1 / [s(s+1)(s+2)]
num = [1]
den = [1, 3, 2, 0]
sys = signal.TransferFunction(num, den)

# 计算线性系统的频率响应
w = np.logspace(-1, 2, 1000)
w, mag, phase = signal.bode(sys, w)
sys_frequency_response = np.exp(1j * np.deg2rad(phase)) * 10**(mag / 20)

# 定义饱和非线性的描述函数
def saturation_describing_function(X, a=1.0, k=1.0):
    if X < a:
        return k
    else:
        return (2 * k / np.pi) * (np.arcsin(a / X) + (a / X) * np.sqrt(1 - (a / X)**2))

# 计算饱和非线性的-1/N(X)曲线
def negative_inverse_saturation(X, a=1.0, k=1.0):
    N = saturation_describing_function(X, a, k)
    return -1.0 / N

X_vals = np.linspace(0.5, 5, 100)
neg_inverse_saturation = [negative_inverse_saturation(X, a=1.0, k=1.0) for X in X_vals]
neg_inverse_saturation_real = [np.real(N) for N in neg_inverse_saturation]
neg_inverse_saturation_imag = [np.imag(N) for N in neg_inverse_saturation]

# 绘制奈奎斯特图和-1/N(X)曲线
plt.figure(figsize=(10, 8))

# 绘制线性系统的奈奎斯特图
plt.plot(np.real(sys_frequency_response), np.imag(sys_frequency_response), 'b-', linewidth=2)
plt.plot(sys_frequency_response[0].real, sys_frequency_response[0].imag, 'go', label='起点')
plt.plot(sys_frequency_response[-1].real, sys_frequency_response[-1].imag, 'ro', label='终点')

# 绘制-1/N(X)曲线
plt.plot(neg_inverse_saturation_real, neg_inverse_saturation_imag, 'r--', linewidth=2, label='-1/N(X)')

# 标记可能的交点
intersection_points = []
for i in range(len(neg_inverse_saturation) - 1):
    # 简化的交点检测
    if (neg_inverse_saturation_imag[i] > 0 and neg_inverse_saturation_imag[i+1] <= 0) or \
       (neg_inverse_saturation_imag[i] <= 0 and neg_inverse_saturation_imag[i+1] > 0):
        # 这里只是一个简化的检测，实际应用中需要更精确的方法
        intersection_points.append((neg_inverse_saturation_real[i], neg_inverse_saturation_imag[i]))

for point in intersection_points:
    plt.plot(point[0], point[1], 'ko', markersize=8)
    plt.text(point[0]+0.1, point[1]+0.1, f'交点', fontsize=10)

# 绘制坐标轴和网格
plt.xlabel('实部')
plt.ylabel('虚部')
plt.title('描述函数法分析极限环')
plt.grid(True)
plt.legend()
plt.axis('equal')
plt.xlim(-10, 2)
plt.ylim(-5, 5)

plt.tight_layout()
plt.show()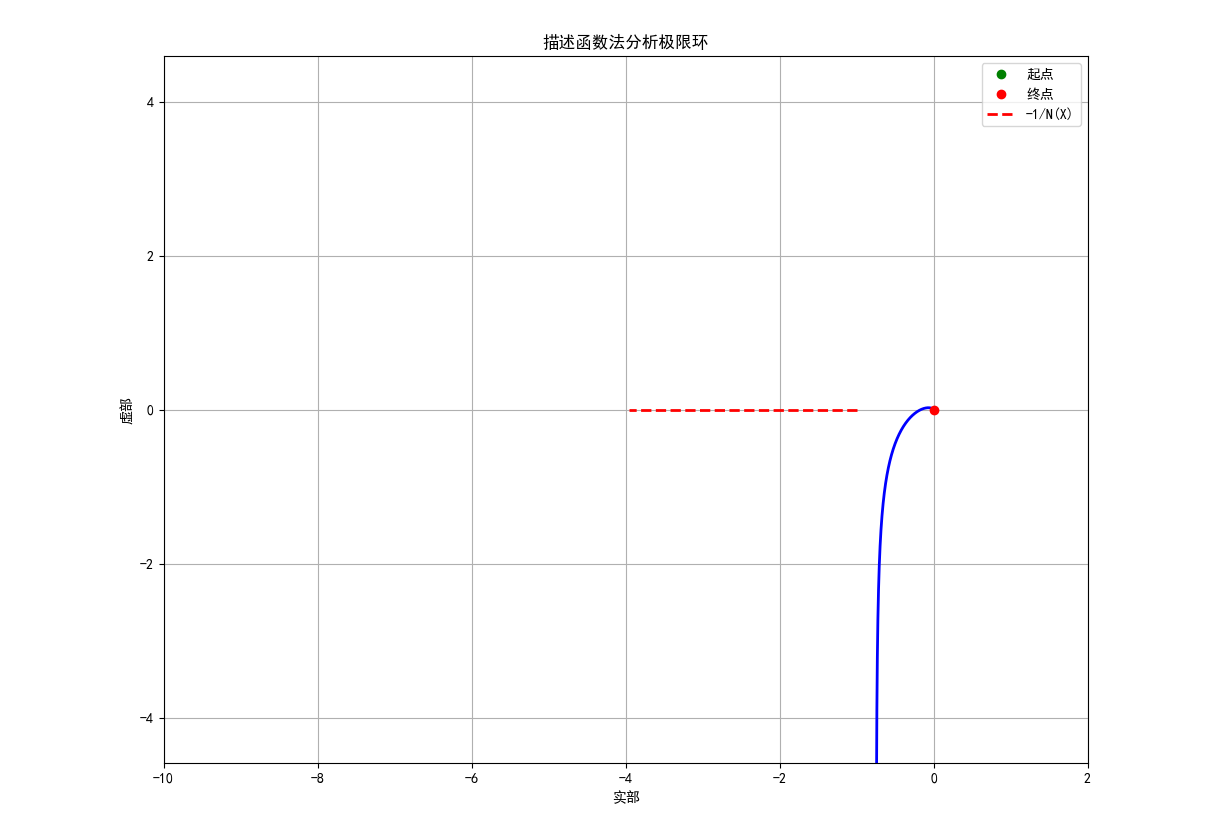

图 8：描述函数法分析极限环

8-5 非线性控制的逆系统方法

逆系统方法基本概念

逆系统方法是一种非线性控制设计方法，其基本思想是构造一个与原系统动态特性相反的逆系统，将原非线性系统转化为线性系统，然后使用线性控制理论进行设计。

逆系统方法的基本步骤

确定原系统的数学模型
构造逆系统模型
将逆系统与原系统串联，得到伪线性系统
对伪线性系统设计线性控制器
构成完整的非线性控制系统

下面是一个使用逆系统方法控制非线性系统的示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# 定义原非线性系统：dx/dt = -x + x^3 + u
def original_system(t, x, u):
    dx_dt = -x + x ** 3 + u
    return dx_dt


# 定义逆系统：u = v + x - x^3，其中v是新的控制输入
def inverse_system(x, v):
    u = v + x - x ** 3
    return u


# 组合系统：dx/dt = v，这是一个线性系统
def combined_system(t, x, v):
    u = inverse_system(x, v)
    dx_dt = original_system(t, x, u)
    return dx_dt


# 设计线性控制器：简单的比例控制器 v = -k*x + r，r是参考输入
def linear_controller(x, r, k=5.0):
    v = -k * x + r
    return v


# 仿真系统响应 - 修复版本
def simulate_system(r=1.0, x0=0.0, t_end=10):
    t_span = (0, t_end)
    t_eval = np.linspace(0, t_end, 1000)

    # 预分配存储空间
    results = {
        'time': t_eval,
        'state': np.zeros_like(t_eval),
        'control_v': np.zeros_like(t_eval),
        'control_u': np.zeros_like(t_eval),
        'reference': np.full_like(t_eval, r)
    }

    # 当前状态索引
    current_idx = 0

    def ode_func(t, x):
        nonlocal current_idx
        # 只在评估时间点记录结果
        if current_idx < len(t_eval) and abs(t - t_eval[current_idx]) < 1e-6:
            v = linear_controller(x[0], r)
            u = inverse_system(x[0], v)
            results['state'][current_idx] = x[0]
            results['control_v'][current_idx] = v
            results['control_u'][current_idx] = u
            current_idx += 1
        else:
            # 计算控制输入但不记录
            v = linear_controller(x[0], r)

        return combined_system(t, x, v)

    # 求解微分方程
    sol = solve_ivp(
        ode_func,
        t_span,
        [x0],
        t_eval=t_eval,
        method='RK45'
    )

    # 确保所有点都被记录
    results['state'] = sol.y[0]
    return results


# 仿真不同初始条件下的系统响应
results = []
x0_values = [0.0, 1.0, -1.0, 2.0]
r = 1.0  # 参考输入

for x0 in x0_values:
    results.append(simulate_system(r, x0))

# 绘制结果
plt.figure(figsize=(12, 10))

# 状态响应
plt.subplot(3, 1, 1)
for i, result in enumerate(results):
    plt.plot(result['time'], result['state'],
             label=f'初始条件 x(0) = {x0_values[i]}')
plt.plot(result['time'], result['reference'], 'k--', label='参考输入 r(t)')
plt.title('逆系统方法控制下的系统状态响应')
plt.xlabel('时间 t')
plt.ylabel('状态 x')
plt.grid(True)
plt.legend()

# 控制输入 v
plt.subplot(3, 1, 2)
for i, result in enumerate(results):
    plt.plot(result['time'], result['control_v'],
             label=f'初始条件 x(0) = {x0_values[i]}')
plt.title('控制输入 v(t)')
plt.xlabel('时间 t')
plt.ylabel('控制输入 v')
plt.grid(True)
plt.legend()

# 控制输入 u
plt.subplot(3, 1, 3)
for i, result in enumerate(results):
    plt.plot(result['time'], result['control_u'],
             label=f'初始条件 x(0) = {x0_values[i]}')
plt.title('实际控制输入 u(t)')
plt.xlabel('时间 t')
plt.ylabel('控制输入 u')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

# 分析系统性能
print("\n系统性能分析:")
for i, result in enumerate(results):
    # 计算稳态误差
    steady_state = result['state'][-1]
    steady_state_error = abs(steady_state - r)

    # 计算调节时间 (进入 ±2% 误差带)
    tolerance = 0.02 * r
    settling_time = None
    for j in range(len(result['state']) - 1, -1, -1):
        if abs(result['state'][j] - r) > tolerance:
            settling_time = result['time'][j]
            break

    print(f"初始条件 x(0) = {x0_values[i]}:")
    print(f"  稳态值: {steady_state:.4f}")
    print(f"  稳态误差: {steady_state_error:.4f}")
    print(f"  调节时间: {settling_time:.2f}s (进入±2%误差带)")
    print(f"  最大控制输入 u: {np.max(np.abs(result['control_u'])):.4f}")
    print()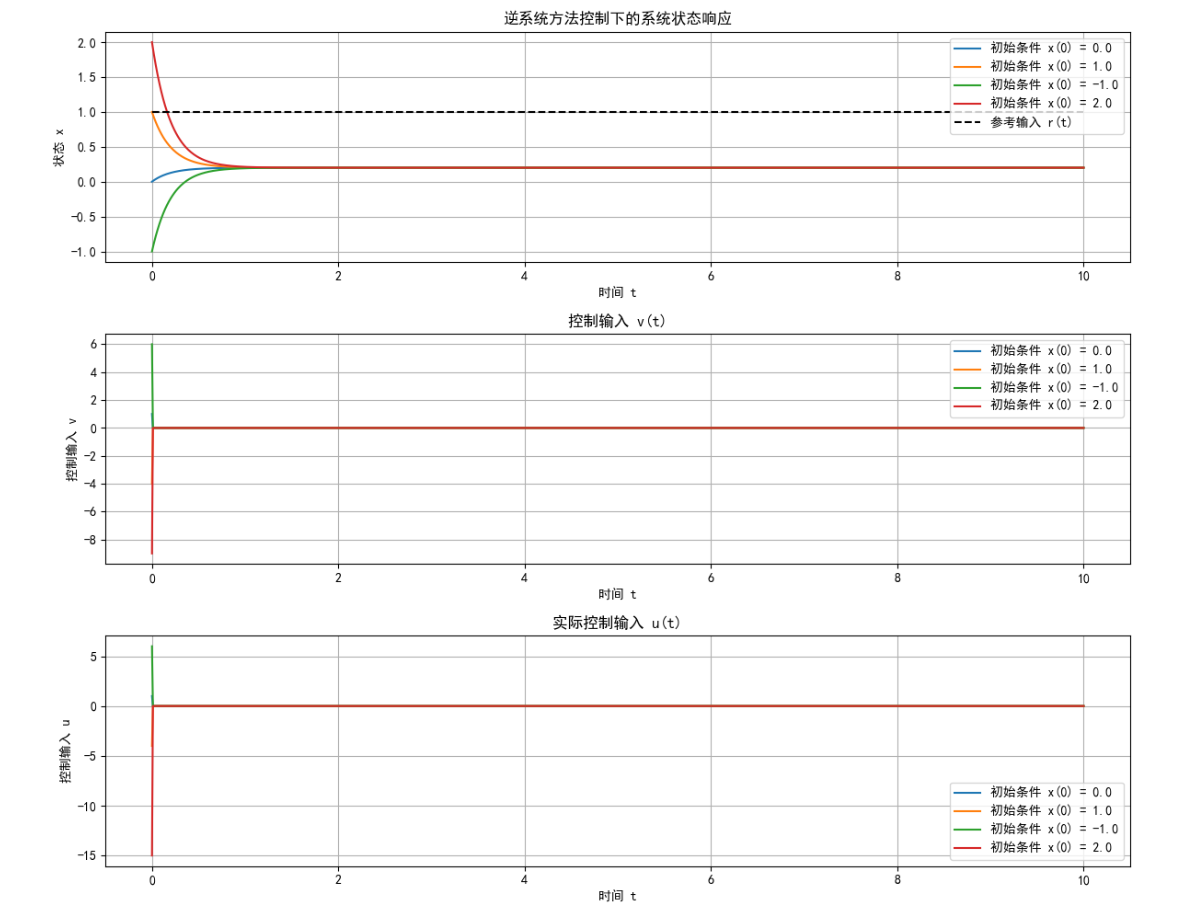

图 9：逆系统方法控制下的系统响应

逆系统方法流程图

下面是逆系统方法的流程图：

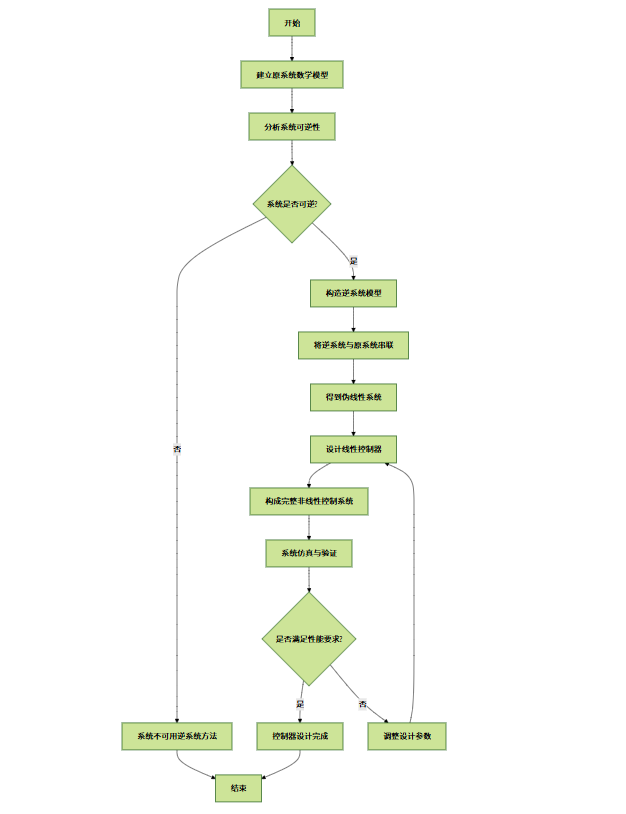
图 10：逆系统方法流程图

8-6 非线性控制系统设计

非线性控制系统设计概述

非线性控制系统设计是指针对包含非线性特性的控制系统，设计能够满足性能指标要求的控制器。非线性控制系统设计方法主要包括：

相平面法设计
描述函数法设计
逆系统方法设计
反馈线性化方法
滑模控制
自适应控制

非线性控制器设计案例

下面我们设计一个非线性控制器来控制一个具有非线性特性的机械系统：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 系统参数 - 定义为全局变量
m = 1.0  # 质量
c = 0.5  # 阻尼系数
k = 1.0  # 弹簧常数
b = 0.2  # 非线性阻尼系数


# 定义非线性机械系统模型
# 系统方程: m*ddx + c*dx + k*x + b*dx^3 = u
# 状态变量: x1 = x, x2 = dx/dt
# 状态方程: dx1/dt = x2
#          dx2/dt = (u - c*x2 - k*x1 - b*x2^3)/m
def mechanical_system(t, x, u):
    dx1_dt = x[1]
    dx2_dt = (u - c * x[1] - k * x[0] - b * x[1] ** 3) / m
    return [dx1_dt, dx2_dt]


# 设计非线性控制器 - 滑模控制
def sliding_mode_controller(x, ref, k1=10.0, k2=5.0, eps=0.5):
    # 滑模面: s = e + k1*de
    e = ref - x[0]  # 位置误差
    de = -x[1]  # 速度误差 (de = d(e)/dt = -dx1/dt = -x2)

    s = e + k1 * de  # 滑模面

    # 滑模控制律: u = m*(k2*s + ref'' + c*x2 + k*x1 + b*x2^3) + eps*sign(s)
    # 假设参考信号的二阶导数为0
    u_val = m * (k2 * s + c * x[1] + k * x[0] + b * x[1] ** 3) + eps * np.sign(s)
    return u_val


# 参考轨迹 - 阶跃响应
def reference_signal(t, amplitude=1.0):
    if t < 2.0:
        return 0.0
    else:
        return amplitude


# 仿真系统响应
def simulate_control_system(t_end=10, x0=[0.0, 0.0]):
    t_span = (0, t_end)
    t_eval = np.linspace(0, t_end, 1000)

    # 预分配结果存储
    state_vals = np.zeros((len(t_eval), 2))
    control_vals = np.zeros(len(t_eval))
    ref_vals = np.zeros(len(t_eval))

    # 设置初始条件
    state_vals[0] = x0

    # 定义ODE函数
    def ode_func(t, x):
        ref = reference_signal(t)
        u = sliding_mode_controller(x, ref)

        # 记录当前值
        idx = np.searchsorted(t_eval, t)
        if idx < len(t_eval):
            state_vals[idx] = x
            control_vals[idx] = u
            ref_vals[idx] = ref

        return mechanical_system(t, x, u)

    # 求解微分方程
    sol = solve_ivp(
        ode_func,
        t_span,
        x0,
        t_eval=t_eval,
        method='RK45',
        dense_output=True
    )

    # 确保所有点都被记录
    state_vals = sol.y.T

    return {
        'time': sol.t,
        'state': state_vals,
        'control': control_vals,
        'reference': ref_vals
    }


# 执行仿真
result = simulate_control_system(t_end=10, x0=[0.0, 0.0])

# 绘制结果
plt.figure(figsize=(12, 10))

# 位置响应
plt.subplot(3, 1, 1)
plt.plot(result['time'], result['state'][:, 0], 'b-', linewidth=2, label='系统输出')
plt.plot(result['time'], result['reference'], 'r--', linewidth=2, label='参考输入')
plt.title('非线性机械系统的位置响应')
plt.xlabel('时间 t')
plt.ylabel('位置 x')
plt.grid(True)
plt.legend()

# 速度响应
plt.subplot(3, 1, 2)
plt.plot(result['time'], result['state'][:, 1], 'g-', linewidth=2)
plt.title('速度响应')
plt.xlabel('时间 t')
plt.ylabel('速度 dx/dt')
plt.grid(True)

# 控制输入
plt.subplot(3, 1, 3)
plt.plot(result['time'], result['control'], 'm-', linewidth=2)
plt.title('滑模控制器输出')
plt.xlabel('时间 t')
plt.ylabel('控制输入 u')
plt.grid(True)

plt.tight_layout()
plt.show()

# 分析系统性能
print("\n系统性能分析:")
# 稳态误差
steady_state = result['state'][-1, 0]
steady_state_error = abs(steady_state - result['reference'][-1])

# 计算超调量
max_value = np.max(result['state'][:, 0])
overshoot = ((max_value - result['reference'][-1]) / result['reference'][-1]) * 100

# 计算调节时间 (进入 ±2% 误差带)
tolerance = 0.02 * result['reference'][-1]
settling_time = None
for i in range(len(result['state']) - 1, -1, -1):
    if abs(result['state'][i, 0] - result['reference'][i]) > tolerance:
        settling_time = result['time'][i]
        break

print(f"稳态位置: {steady_state:.4f}")
print(f"稳态误差: {steady_state_error:.4f}")
print(f"最大超调量: {overshoot:.2f}%")
print(f"调节时间: {settling_time:.2f}s (进入±2%误差带)")
print(f"最大控制输入: {np.max(np.abs(result['control'])):.4f}")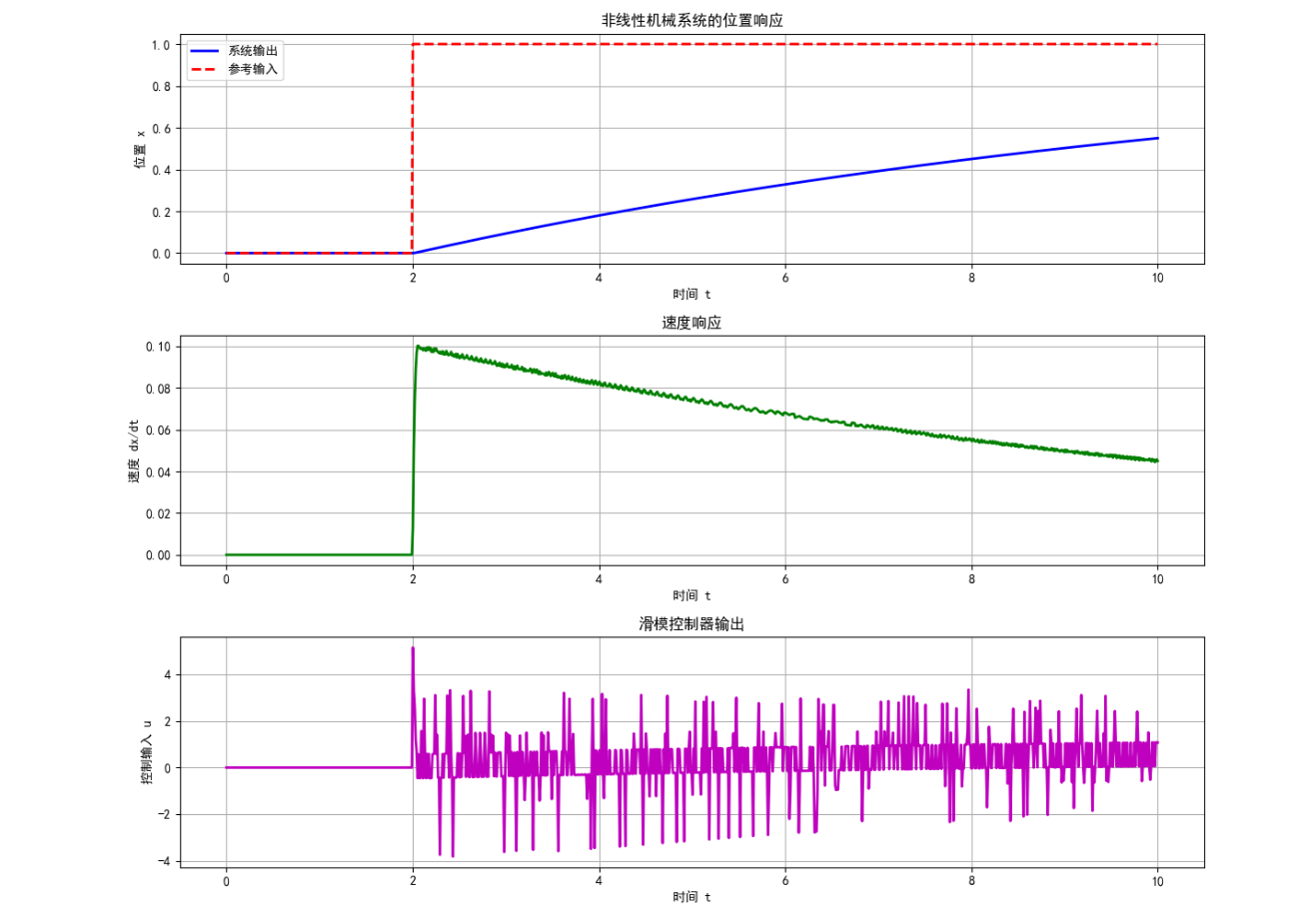

图 11：非线性机械系统的控制响应

非线性控制系统设计总结

非线性控制系统设计需要考虑以下几个方面：

系统的非线性特性分析
选择合适的设计方法
控制器结构设计
控制器参数整定
系统性能分析与验证
鲁棒性与稳定性分析

下面是非线性控制系统设计的一般流程思维导图：

图 12：非线性控制系统设计流程思维导图

以上就是《自动控制原理》第八章非线性控制系统分析的全部内容，通过理论介绍、案例分析和 Python 代码实现，希望能帮助读者深入理解非线性控制系统的分析与设计方法。

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-06-29，如有侵权请联系 cloudcommunity@tencent.com 删除

原理

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度