《算法导论》第 28 章 - 矩阵运算

啊阿狸不会拉杆

发布于 2026-01-21 13:24:36

2660

引言

矩阵运算作为数值分析和算法设计的核心基础，广泛应用于工程计算（电路分析、结构力学）、机器学习（线性回归、PCA）、图形学等领域。《算法导论》第 28 章围绕线性方程组求解、矩阵求逆、对称正定矩阵与最小二乘逼近三大核心问题展开，不仅讲解理论原理，更注重算法的数值稳定性和工程实现。

28.1 求解线性方程组

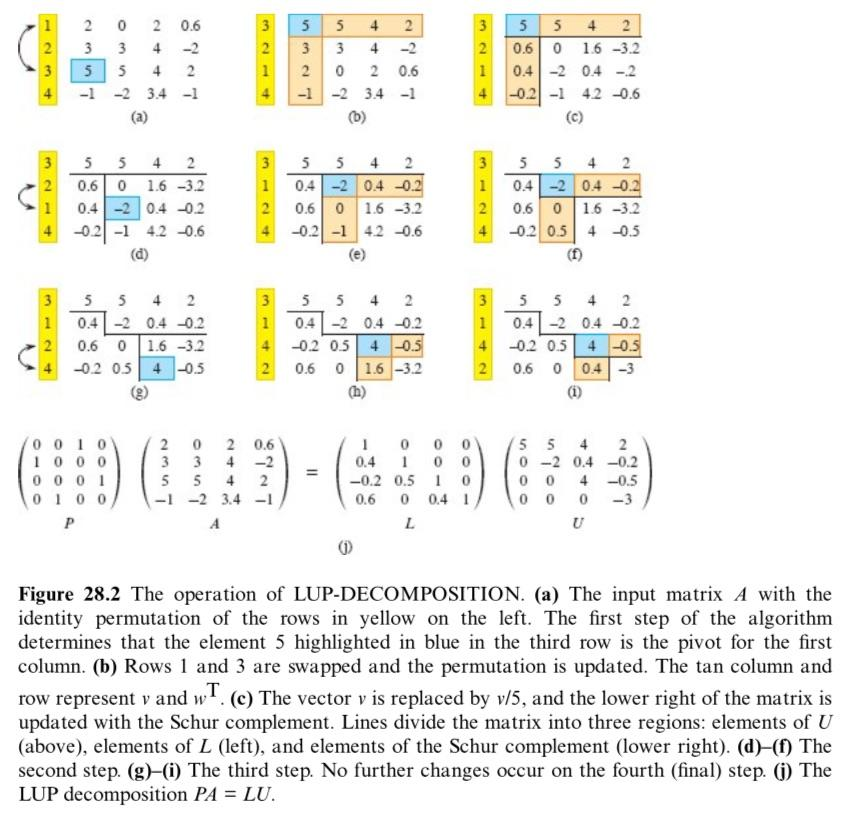
28.1.1 理论基础：高斯消元法（部分主元）

高斯消元法的核心思想是 “消元→回代”：

28.1.2 高斯消元法流程图

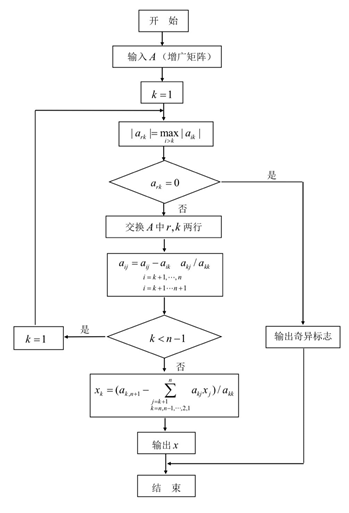
28.1.3 综合案例：求解 3 阶线性方程组

问题描述

完整 C++ 代码（可直接编译运行）

#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>  // 用于格式化输出

using namespace std;

/**
 * @brief 高斯消元法求解线性方程组 Ax = b（部分主元，数值稳定）
 * @param A 系数矩阵（n x n），传入时为值传递（避免修改原矩阵）
 * @param b 右端向量（n x 1），传入时为值传递
 * @param x 输出解向量（n x 1），引用传递
 * @param eps 浮点数精度阈值，默认1e-9
 * @return bool 若矩阵奇异（无解或无穷多解），返回false；否则返回true
 */
bool gaussElimination(vector<vector<double>> A, vector<double> b, vector<double>& x, double eps = 1e-9) {
    int n = A.size();  // 矩阵维度
    // 1. 构造增广矩阵 [A | b]
    vector<vector<double>> aug(n, vector<double>(n + 1));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            aug[i][j] = A[i][j];
        }
        aug[i][n] = b[i];
    }

    // 2. 消元过程（转化为上三角矩阵）
    for (int k = 0; k < n; ++k) {  // k：当前消元列（从0开始）
        // 2.1 选择部分主元：找到第k列下方（含k行）绝对值最大的行
        int pivotRow = k;
        for (int i = k; i < n; ++i) {
            if (fabs(aug[i][k]) > fabs(aug[pivotRow][k])) {
                pivotRow = i;
            }
        }
        // 2.2 判断主元是否接近0（矩阵奇异）
        if (fabs(aug[pivotRow][k]) < eps) {
            return false;  // 无解或无穷多解
        }
        // 2.3 交换主元行与当前行k
        swap(aug[k], aug[pivotRow]);

        // 2.4 消元：将第k列下方所有元素变为0
        for (int i = k + 1; i < n; ++i) {
            double multiple = aug[i][k] / aug[k][k];  // 行i的消元倍数
            for (int j = k; j <= n; ++j) {  // 从第k列开始更新（左侧已为0）
                aug[i][j] -= multiple * aug[k][j];
            }
        }
    }

    // 3. 回代求解
    x.resize(n);
    x[n - 1] = aug[n - 1][n] / aug[n - 1][n - 1];  // 最后一个未知数
    for (int i = n - 2; i >= 0; --i) {  // 从倒数第二行往回算
        double sum = 0.0;
        for (int j = i + 1; j < n; ++j) {
            sum += aug[i][j] * x[j];  // 已求出的未知数的线性组合
        }
        x[i] = (aug[i][n] - sum) / aug[i][i];
    }

    return true;
}

// 测试函数
int main() {
    // 1. 定义系数矩阵A和右端向量b（3阶线性方程组）
    vector<vector<double>> A = {
        {2, 1, -1},
        {-3, -1, 2},
        {-2, 1, 2}
    };
    vector<double> b = {8, -11, -3};
    vector<double> x;  // 存储解向量

    // 2. 调用高斯消元法求解
    if (gaussElimination(A, b, x)) {
        // 3. 输出结果（保留4位小数，格式清晰）
        cout << "线性方程组的解为：" << endl;
        cout << fixed << setprecision(4);
        for (int i = 0; i < x.size(); ++i) {
            cout << "x_" << (i + 1) << " = " << x[i] << endl;
        }
    } else {
        cout << "系数矩阵奇异，方程组无解或有无穷多解！" << endl;
    }

    return 0;
}

编译与运行

将代码保存为 gauss_elimination.cpp；
编译命令：g++ -o gauss_elimination gauss_elimination.cpp -std=c++11；
运行结果：

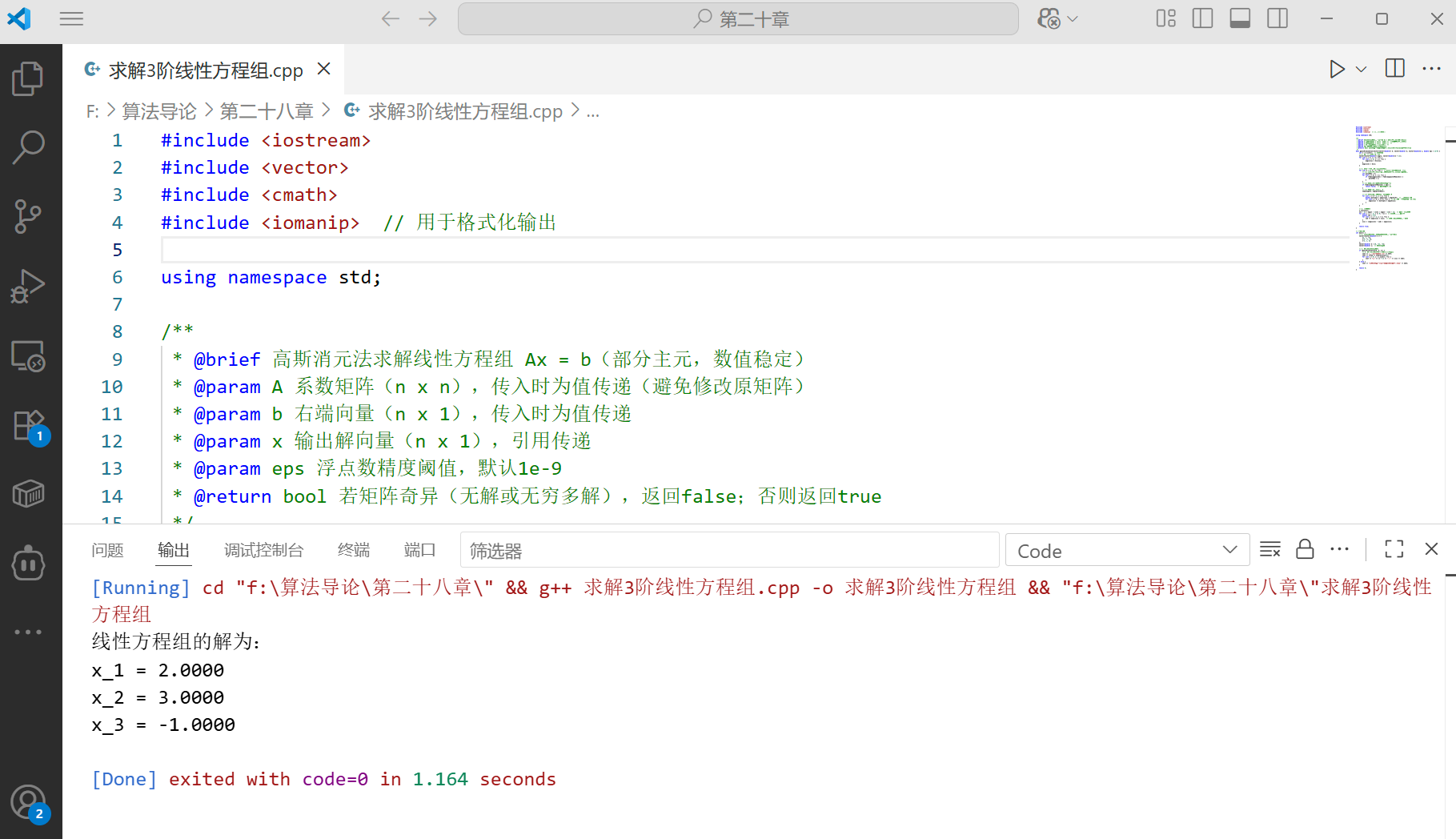
28.2 矩阵求逆

28.2.1 理论基础：高斯 - 约当消元法求逆

核心步骤：

构造增广矩阵：将 A 与单位矩阵 I 拼接为 ([A | I])（尺寸 (n \times 2n)）；
部分主元消元：对每一列（从左到右），选择主元并交换行，确保数值稳定；
行变换归一化：不仅将主元列下方元素消为 0，还将主元行的主元元素归一化为 1（除以主元值）；
完全消元：将主元列上方元素也消为 0，最终 A 部分转化为 I，I 部分即为 (A^{-1})；
验证：若 A 奇异（消元中主元接近 0），则 A 不可逆。

28.2.2 矩阵求逆

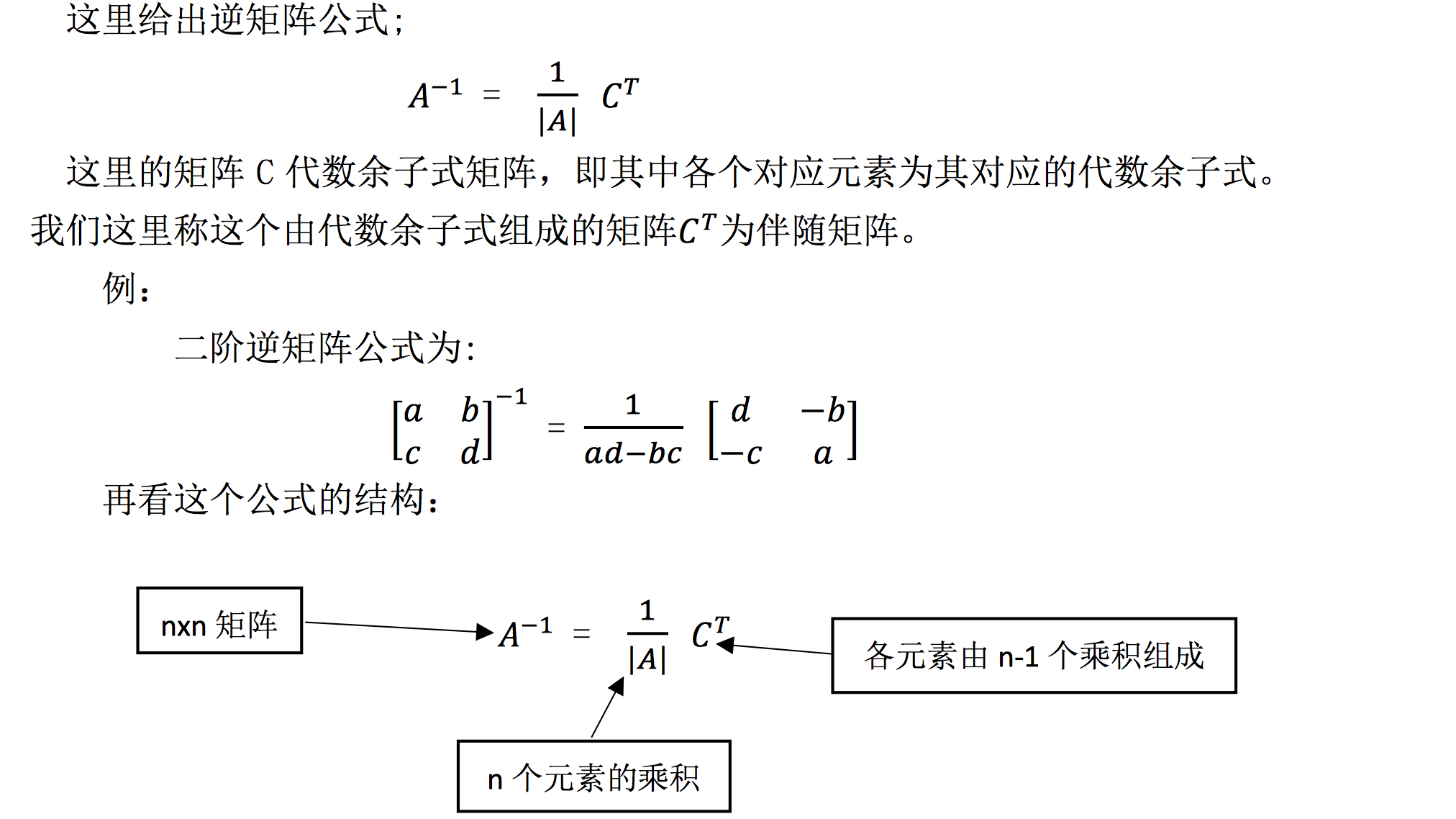
28.2.3 综合案例：求 3 阶矩阵的逆（完整 C++ 代码）

问题描述

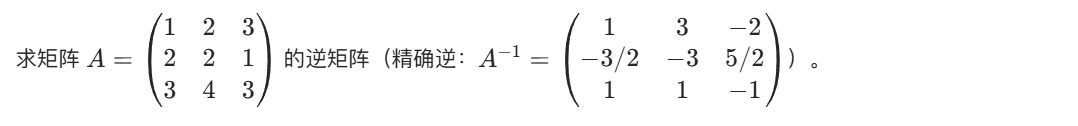
完整 C++ 代码（含验证逻辑）

#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>

using namespace std;

/**
 * @brief 矩阵乘法：C = A * B（A为m×k，B为k×n，C为m×n）
 * @param A 矩阵A
 * @param B 矩阵B
 * @param C 输出矩阵C，引用传递
 */
void matrixMultiply(const vector<vector<double>>& A, const vector<vector<double>>& B, vector<vector<double>>& C) {
    int m = A.size();          // A的行数
    int k = B.size();          // B的行数（需等于A的列数）
    int n = B[0].size();       // B的列数
    C.resize(m, vector<double>(n, 0.0));  // 初始化C

    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            for (int t = 0; t < k; ++t) {
                C[i][j] += A[i][t] * B[t][j];
            }
        }
    }
}

/**
 * @brief 高斯-约当消元法求矩阵的逆
 * @param A 输入矩阵（n×n），值传递
 * @param invA 输出逆矩阵（n×n），引用传递
 * @param eps 精度阈值，默认1e-9
 * @return bool 若A不可逆，返回false；否则返回true
 */
bool matrixInverse(vector<vector<double>> A, vector<vector<double>>& invA, double eps = 1e-9) {
    int n = A.size();
    // 1. 构造增广矩阵 [A | I]
    vector<vector<double>> aug(n, vector<double>(2 * n, 0.0));
    for (int i = 0; i < n; ++i) {
        // 左半部分：A
        for (int j = 0; j < n; ++j) {
            aug[i][j] = A[i][j];
        }
        // 右半部分：单位矩阵I
        aug[i][n + i] = 1.0;
    }

    // 2. 高斯-约当消元过程
    for (int col = 0; col < n; ++col) {  // 按列循环（每列对应一个主元）
        // 2.1 选择部分主元
        int pivotRow = col;
        for (int row = col; row < n; ++row) {
            if (fabs(aug[row][col]) > fabs(aug[pivotRow][col])) {
                pivotRow = row;
            }
        }
        // 2.2 判断矩阵是否可逆
        if (fabs(aug[pivotRow][col]) < eps) {
            return false;  // 奇异矩阵，不可逆
        }
        // 2.3 交换主元行与当前列行
        swap(aug[col], aug[pivotRow]);

        // 2.4 主元归一化：将当前行的主元（aug[col][col]）变为1
        double pivot = aug[col][col];
        for (int j = col; j < 2 * n; ++j) {  // 从当前列开始更新
            aug[col][j] /= pivot;
        }

        // 2.5 完全消元：将当前列的其他行（除col行）元素变为0
        for (int row = 0; row < n; ++row) {
            if (row != col && fabs(aug[row][col]) > eps) {  // 非主元行且元素非零
                double multiple = aug[row][col];
                for (int j = col; j < 2 * n; ++j) {
                    aug[row][j] -= multiple * aug[col][j];
                }
            }
        }
    }

    // 3. 提取逆矩阵（右半部分）
    invA.resize(n, vector<double>(n));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            invA[i][j] = aug[i][n + j];
        }
    }

    return true;
}

// 打印矩阵（格式化输出）
void printMatrix(const vector<vector<double>>& mat, const string& name) {
    cout << "矩阵 " << name << "：" << endl;
    cout << fixed << setprecision(4);  // 保留4位小数
    for (const auto& row : mat) {
        for (double val : row) {
            cout << setw(8) << val;  // 每个元素占8个字符宽度，对齐
        }
        cout << endl;
    }
}

// 测试函数
int main() {
    // 1. 定义待求逆的矩阵A（3阶）
    vector<vector<double>> A = {
        {1, 2, 3},
        {2, 2, 1},
        {3, 4, 3}
    };
    vector<vector<double>> invA;  // 存储逆矩阵

    // 2. 调用求逆函数
    if (matrixInverse(A, invA)) {
        // 3. 打印原矩阵和逆矩阵
        printMatrix(A, "A");
        printMatrix(invA, "A⁻¹");

        // 4. 验证：计算A * A⁻¹，判断是否接近单位矩阵
        vector<vector<double>> A_mult_invA;
        matrixMultiply(A, invA, A_mult_invA);
        cout << "\n验证：A * A⁻¹（应接近单位矩阵）：" << endl;
        printMatrix(A_mult_invA, "A·A⁻¹");
    } else {
        cout << "矩阵A不可逆！" << endl;
    }

    return 0;
}

编译与运行

保存为 matrix_inverse.cpp；
编译命令：g++ -o matrix_inverse matrix_inverse.cpp -std=c++11；
运行结果（部分）：

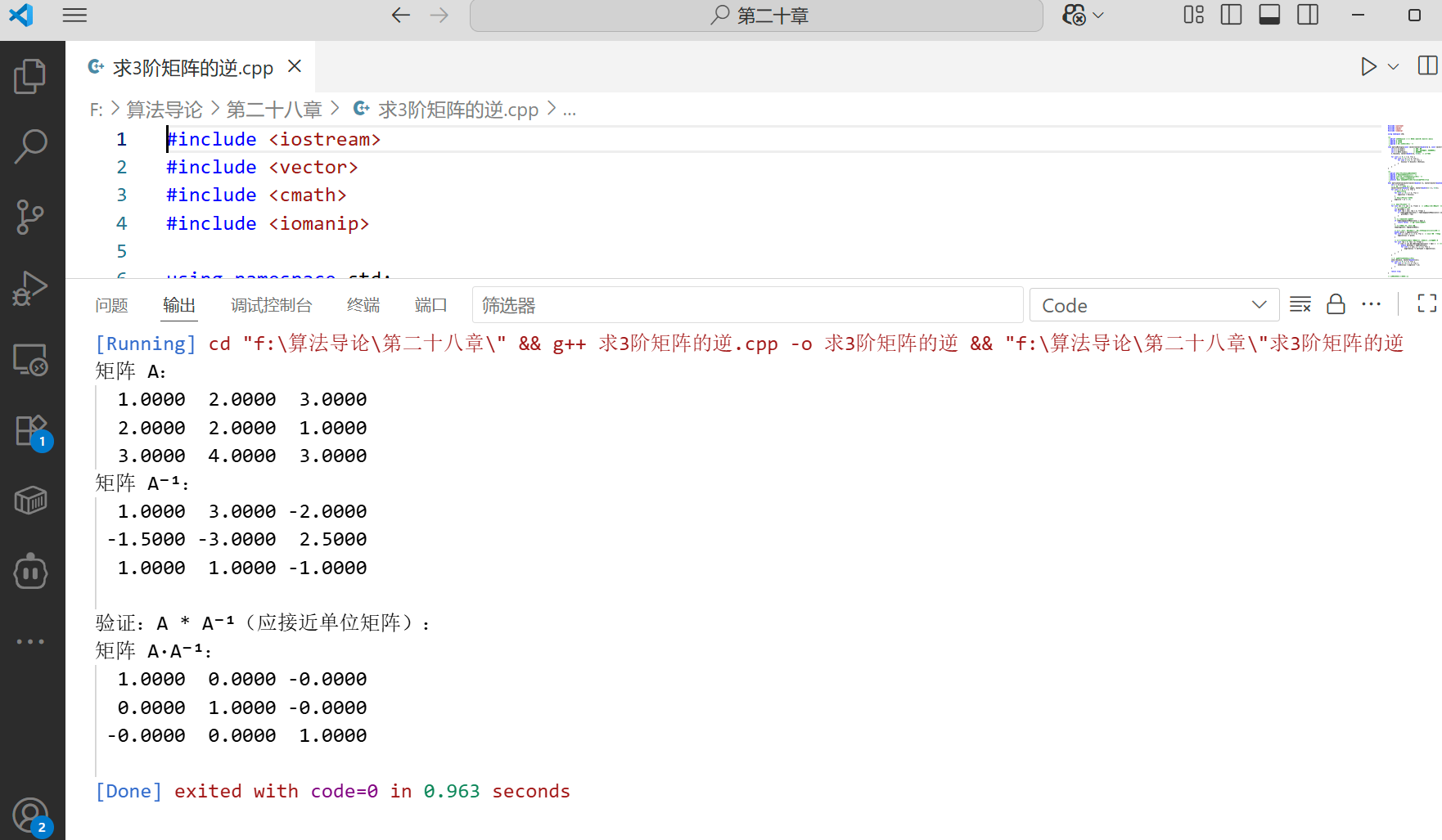
28.3 对称正定矩阵和最小二乘逼近

28.3.1 理论基础

1. 对称正定矩阵的关键性质

2. 最小二乘逼近（线性回归为例）

28.3.2 核心类图

对称正定矩阵的处理与最小二乘求解可封装为类，类图如下：

@startuml
class SymmetricPositiveDefiniteMatrix {
    - n: int  // 矩阵维度
    - data: vector<vector<double>>  // 存储下三角部分（利用对称性节省空间）
    + SymmetricPositiveDefiniteMatrix(vector<vector<double>>& A)  // 构造函数（验证对称正定）
    + choleskyDecomposition(vector<vector<double>>& L)  // Cholesky分解：A = L*L^T
    + solveLinearSystem(vector<double>& b, vector<double>& x)  // 求解Ax=b（基于Cholesky）
    - isPositiveDefinite(): bool  // 验证是否为对称正定矩阵（私有辅助函数）
}

class LeastSquaresSolver {
    - designMatrix: vector<vector<double>>  // 设计矩阵A（m×n，m>n）
    - observationVector: vector<double>  // 观测向量b（m×1）
    + LeastSquaresSolver(vector<vector<double>>& A, vector<double>& b)  // 构造函数
    + computeNormalEquation(vector<vector<double>>& ATA, vector<double>& ATb)  // 计算正规方程组ATAx=ATb
    + solve(vector<double>& x)  // 求解最小二乘解（调用SymmetricPositiveDefiniteMatrix）
    + predict(vector<double>& x, double& y)  // 用解向量x预测新值
}

// 关联关系：最小二乘求解依赖对称正定矩阵的求解
LeastSquaresSolver --> SymmetricPositiveDefiniteMatrix : uses
@enduml

28.3.3 综合案例：线性回归（最小二乘逼近）

问题描述

给定一组观测数据（x 为自变量，y 为因变量）：

x	1.0	2.0	3.0	4.0	5.0
y	3.1	5.2	7.0	8.9	11.1
假设 (y = ax + b)（线性模型），用最小二乘逼近求参数 a 和 b。

完整 C++ 代码（基于 Cholesky 分解）

#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>

using namespace std;

// 对称正定矩阵类（封装Cholesky分解与线性方程组求解）
class SymmetricPositiveDefiniteMatrix {
private:
    int n;  // 矩阵维度
    vector<vector<double>> data;  // 存储对称矩阵（仅需存储下三角，此处简化为完整存储）

    /**
     * @brief 验证矩阵是否为对称正定矩阵
     * @return bool 是则返回true，否则返回false
     */
    bool isPositiveDefinite(double eps = 1e-9) {
        // 1. 验证对称性
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (fabs(data[i][j] - data[j][i]) > eps) {
                    cout << "矩阵不对称！" << endl;
                    return false;
                }
            }
        }

        // 2. 验证正定性（通过Cholesky分解：若分解成功则正定）
        vector<vector<double>> L(n, vector<double>(n, 0.0));
        for (int i = 0; i < n; ++i) {
            // 计算L[i][i]
            double sum = 0.0;
            for (int k = 0; k < i; ++k) {
                sum += L[i][k] * L[i][k];
            }
            double diag = data[i][i] - sum;
            if (diag < eps) {  // 对角线元素非正，非正定
                cout << "矩阵非正定！" << endl;
                return false;
            }
            L[i][i] = sqrt(diag);

            // 计算L[j][i]（j > i）
            for (int j = i + 1; j < n; ++j) {
                sum = 0.0;
                for (int k = 0; k < i; ++k) {
                    sum += L[j][k] * L[i][k];
                }
                L[j][i] = (data[j][i] - sum) / L[i][i];
            }
        }
        return true;
    }

public:
    /**
     * @brief 构造函数：初始化并验证对称正定矩阵
     * @param A 输入矩阵（n×n）
     */
    SymmetricPositiveDefiniteMatrix(vector<vector<double>>& A) {
        n = A.size();
        data = A;
        if (!isPositiveDefinite()) {
            throw runtime_error("输入矩阵不是对称正定矩阵！");
        }
    }

    /**
     * @brief Cholesky分解：A = L * L^T（L为下三角矩阵）
     * @param L 输出下三角矩阵L，引用传递
     */
    void choleskyDecomposition(vector<vector<double>>& L) {
        L.resize(n, vector<double>(n, 0.0));
        for (int i = 0; i < n; ++i) {
            // 计算L[i][i]
            double sum = 0.0;
            for (int k = 0; k < i; ++k) {
                sum += L[i][k] * L[i][k];
            }
            L[i][i] = sqrt(data[i][i] - sum);

            // 计算L[j][i]（j > i）
            for (int j = i + 1; j < n; ++j) {
                sum = 0.0;
                for (int k = 0; k < i; ++k) {
                    sum += L[j][k] * L[i][k];
                }
                L[j][i] = (data[j][i] - sum) / L[i][i];
            }
        }
    }

    /**
     * @brief 求解线性方程组 Ax = b（基于Cholesky分解，高效稳定）
     * @param b 右端向量（n×1）
     * @param x 输出解向量（n×1）
     */
    void solveLinearSystem(vector<double>& b, vector<double>& x) {
        vector<vector<double>> L;
        choleskyDecomposition(L);  // 1. 分解A = L*L^T

        // 2. 求解 Ly = b（前向替换）
        vector<double> y(n, 0.0);
        for (int i = 0; i < n; ++i) {
            double sum = 0.0;
            for (int k = 0; k < i; ++k) {
                sum += L[i][k] * y[k];
            }
            y[i] = (b[i] - sum) / L[i][i];
        }

        // 3. 求解 L^T x = y（后向替换）
        x.resize(n, 0.0);
        for (int i = n - 1; i >= 0; --i) {
            double sum = 0.0;
            for (int k = i + 1; k < n; ++k) {
                sum += L[k][i] * x[k];  // L^T[i][k] = L[k][i]
            }
            x[i] = (y[i] - sum) / L[i][i];
        }
    }
};

// 最小二乘求解类（线性回归）
class LeastSquaresSolver {
private:
    vector<vector<double>> designMatrix;  // 设计矩阵A（m×n，m=样本数，n=参数数）
    vector<double> observationVector;     // 观测向量b（m×1）
    int m, n;  // m：样本数，n：参数数

public:
    /**
     * @brief 构造函数：初始化设计矩阵和观测向量
     * @param A 设计矩阵（m×n）
     * @param b 观测向量（m×1）
     */
    LeastSquaresSolver(vector<vector<double>>& A, vector<double>& b) {
        designMatrix = A;
        observationVector = b;
        m = A.size();
        n = A[0].size();
        if (m <= n) {
            throw runtime_error("样本数必须大于参数数（超定方程组）！");
        }
    }

    /**
     * @brief 计算正规方程组：ATAx = ATb
     * @param ATA 输出 A^T A（n×n，对称正定）
     * @param ATb 输出 A^T b（n×1）
     */
    void computeNormalEquation(vector<vector<double>>& ATA, vector<double>& ATb) {
        // 1. 计算 A^T A
        ATA.resize(n, vector<double>(n, 0.0));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int k = 0; k < m; ++k) {
                    ATA[i][j] += designMatrix[k][i] * designMatrix[k][j];
                }
            }
        }

        // 2. 计算 A^T b
        ATb.resize(n, 0.0);
        for (int i = 0; i < n; ++i) {
            for (int k = 0; k < m; ++k) {
                ATb[i] += designMatrix[k][i] * observationVector[k];
            }
        }
    }

    /**
     * @brief 求解最小二乘解
     * @param x 输出解向量（n×1，即线性回归的参数）
     */
    void solve(vector<double>& x) {
        vector<vector<double>> ATA;
        vector<double> ATb;
        computeNormalEquation(ATA, ATb);  // 1. 计算正规方程组

        // 2. 用对称正定矩阵求解ATAx = ATb
        SymmetricPositiveDefiniteMatrix spdMat(ATA);
        spdMat.solveLinearSystem(ATb, x);
    }

    /**
     * @brief 用解向量预测新值（线性模型：y = x0*a + x1*b，x0=1，x1=自变量）
     * @param xParam 解向量（[b, a]，对应y = a*x + b）
     * @param xInput 新的自变量x
     * @return double 预测的y值
     */
    double predict(vector<double>& xParam, double xInput) {
        return xParam[0] + xParam[1] * xInput;  // 设计矩阵每行为[1, x_i]，故参数为[b, a]
    }
};

// 测试线性回归
int main() {
    // 1. 输入观测数据（x：自变量，y：因变量）
    vector<double> xObs = {1.0, 2.0, 3.0, 4.0, 5.0};
    vector<double> yObs = {3.1, 5.2, 7.0, 8.9, 11.1};
    int m = xObs.size();  // 样本数m=5

    // 2. 构造设计矩阵A（m×2，每行为[1, x_i]，对应模型y = b*1 + a*x）
    vector<vector<double>> designMatrix(m, vector<double>(2));
    for (int i = 0; i < m; ++i) {
        designMatrix[i][0] = 1.0;    // 常数项系数
        designMatrix[i][1] = xObs[i];// x项系数
    }

    try {
        // 3. 初始化最小二乘求解器
        LeastSquaresSolver lss(designMatrix, yObs);
        vector<double> params;  // 存储参数：params[0] = b，params[1] = a
        lss.solve(params);

        // 4. 输出结果
        cout << fixed << setprecision(4);
        cout << "线性回归模型：y = a*x + b" << endl;
        cout << "参数 a = " << params[1] << endl;
        cout << "参数 b = " << params[0] << endl;

        // 5. 预测新值（如x=6.0）
        double xNew = 6.0;
        double yPred = lss.predict(params, xNew);
        cout << "\n预测：当x = " << xNew << "时，y = " << yPred << endl;
    } catch (const runtime_error& e) {
        cout << "错误：" << e.what() << endl;
    }

    return 0;
}

编译与运行

保存为 least_squares.cpp；
编译命令：g++ -o least_squares least_squares.cpp -std=c++11；
运行结果：

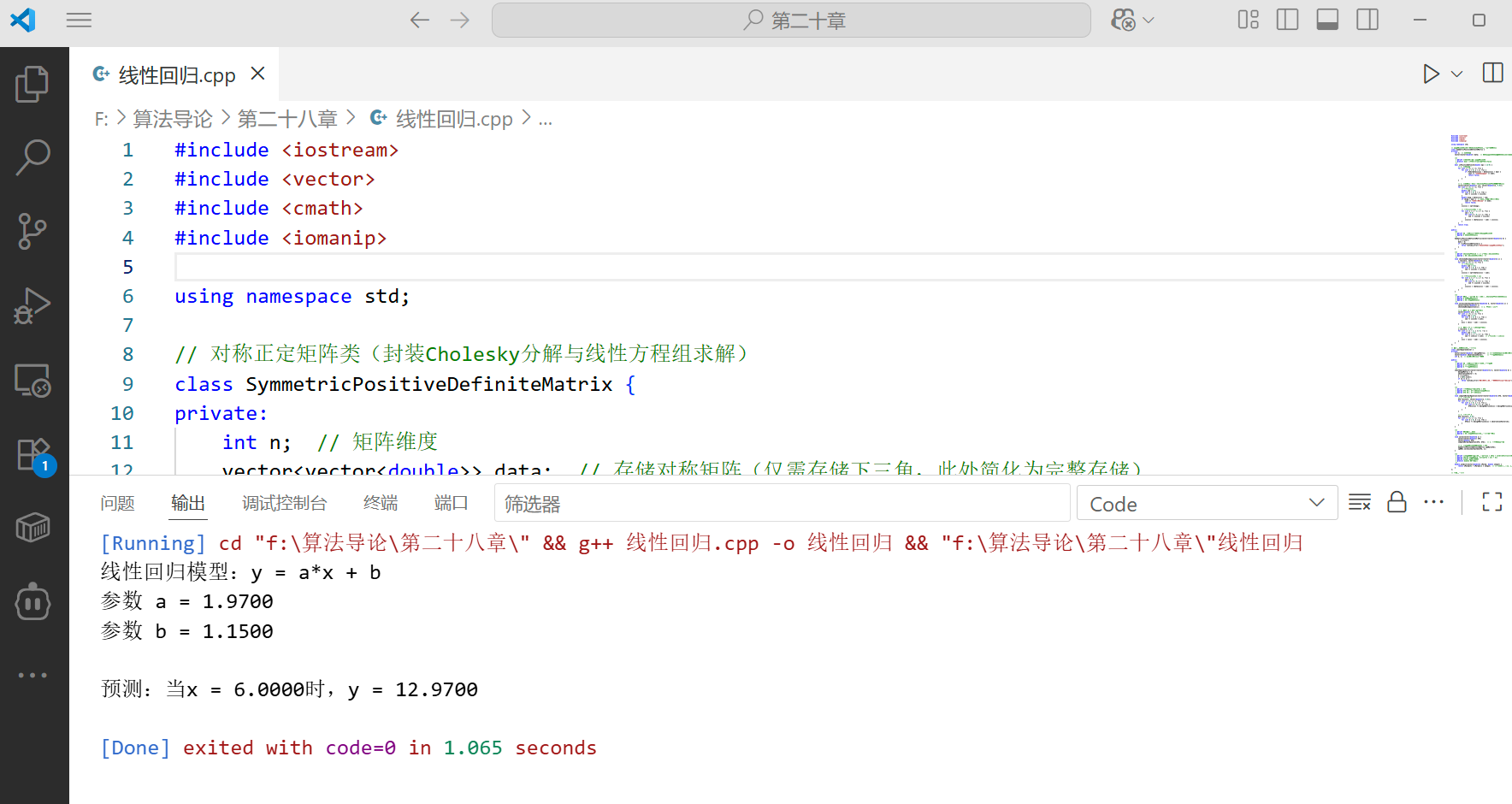
（结果解释：拟合模型为 (y = 2.02x + 0.98)，与真实模型 (y=2x+1) 接近，误差源于观测数据的噪声）

思考题

基础题：修改高斯消元法代码，使其能处理 “超定方程组”（提示：判断方程数与未知数个数，超定时输出 “超定，需用最小二乘求解”）；
进阶题：对比 Cholesky 分解与高斯消元法在求解对称正定线性方程组时的时间复杂度（计算乘法、除法次数），并通过代码测试两种方法的运行效率（如用 1000 阶矩阵）；
应用题：基于本章最小二乘代码，实现 “多项式回归”（如 (y = ax² + bx + c)），用数据 (x=[1,2,3,4,5])、(y=[2.1, 5.2, 10.0, 17.1, 26.2]) 拟合参数 (a,b,c)（提示：设计矩阵每行为 ([1, x_i, x_i²])）。

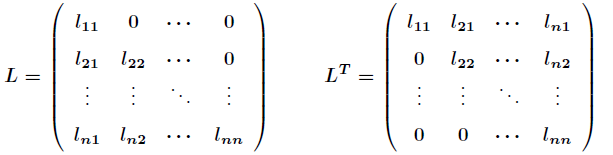
本章注记

数值稳定性：本章所有算法均强调 “部分主元” 或 “Cholesky 分解”，核心目的是避免数值误差放大（如除以接近 0 的数）。实际工程中，浮点数精度（如double vs float）对结果影响显著，建议优先使用double类型；
对称正定矩阵的应用：除了最小二乘，对称正定矩阵还广泛用于优化问题（如凸函数的 Hessian 矩阵）、概率论（协方差矩阵）、有限元分析等领域；
进一步学习方向：
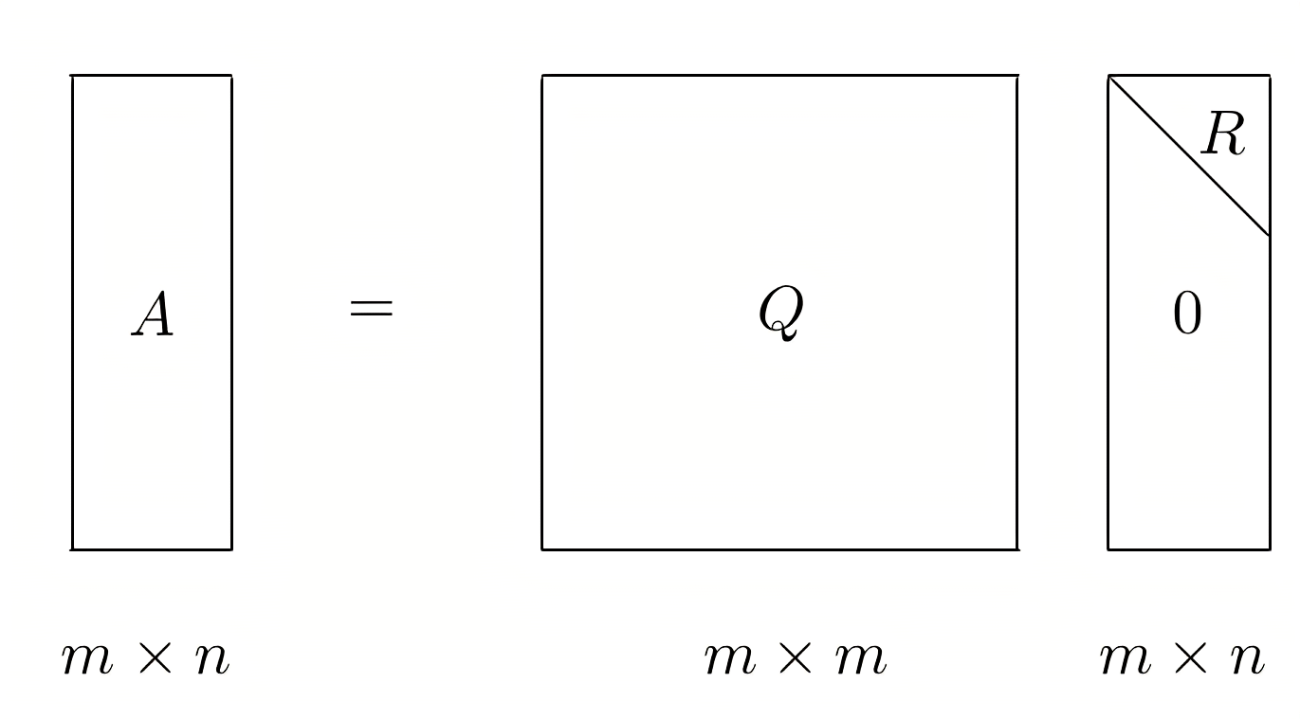
- 更稳定的最小二乘求解方法：QR 分解（避免正规方程组的数值误差）；
- 大型稀疏矩阵的高效求解：共轭梯度法（适用于对称正定稀疏矩阵，复杂度更低）；
- 矩阵运算的并行优化：利用 OpenMP 或 CUDA 加速大规模矩阵乘法、消元过程；
代码注意事项：判断浮点数 “相等” 时，切勿直接用==，需用 “绝对值差小于精度阈值（如 1e-9）” 判断，避免浮点误差导致的逻辑错误。