深度学习之注意力机制中QKV原理解读

引言

在自注意力（Self-Attention）机制中，查询（Query，简称Q）、键（Key，简称K）和值（Value，简称V）是三个核心的概念，它们共同参与计算以生成序列的加权表示。上篇文章里面有过对QKV的一些简单介绍，但是还不够深入，因为其占据了注意力机制的“半壁江山”，现在前沿的大模型研究工作很大一部分都是围绕着QKV矩阵去做的，比如注意力、量化、低秩压缩等等。

其本质原因是因为QKV权重占比着大语言模型50%以上的权重比例，在推理过程中，QKV存储量还会随着上下文长度的增长而线性增长，计算量也平方增加。

那么问题来了：

QKV 机制到底是在干什么？它们各自的输出是什么？最终的注意力输出又代表什么？ QKV在哪里？为什么需要QKV?

01、单头注意力机制下的QKV机制

假设你现在在读一段话：

“小明昨天去了学校，他今天也去了学校。”

你看到“他今天也去了学校”中的“他”，想知道“他”指的是谁。这时候，“他”就是你的 Query。

然后你回头去看前面的句子，“小明昨天去了学校”，这句话的 Key 就可能是“小明”，因为它回答了“他是谁”的问题。

而 Value 就是整句话的内容：“小明昨天去了学校”。

所以注意力机制就是在做这样的事情：

给定一个 Query，找到与之匹配的 Key，并从中提取对应的 Value。

在 Transformer 中，注意力机制的核心就是通过三个向量：Query、Key 和 Value 来计算出哪些信息更重要，更值得被关注。

我们先来梳理一下整体流程：

假设我们有一个序列，包含n个元素，每个元素用一个d维向量表示。那么整个序列可以表示为一个n×d的矩阵X。

然后，我们通过三个不同的线性变换（矩阵）将X变换为Q、K、V：

• Q = X * W_Q
• K = X * W_K
• V = X * W_V

其中W_Q, W_K, W_V是在模型训练中可学习的参数矩阵，是模型在训练过程中“慢慢学出来的数字”——初始是随机值，训练时会根据任务（比如翻译、文本理解）不断调整，直到Q/K/V能准确计算出“词与词的关联度”。

然后，我们计算注意力分数：对于每个查询向量q_i（对应第i个元素），我们计算它与所有键向量k_j的点积，然后除以根号下d_k（为了梯度稳定），再通过softmax归一化，得到权重α_ij。这些权重就是注意力分数，表示第i个元素与第j个元素的相关程度。

最后，对于第i个元素，我们使用权重α_ij对所有的值向量v_j进行加权求和，得到输出z_i。

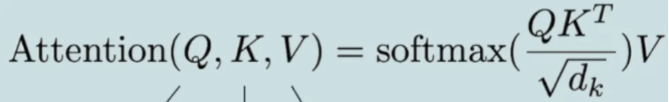
将Q理解成查询，就是你想要查询什么？

将K理解成索引标签，相当于书的目录，记录了书中内容的位置。

将V理解成每个位置的实际内容，也就是你真正想获取的信息。

这样是不是就好理解了，这样我再举个实际的例子就更容易明白了。我将采用单头注意力机制和交叉注意力机制两种进行说明，交叉注意力机制为多模态模型Transformer架构机制，后续会单独出一篇文章进行说明。

假设我们有一组狗狗的照片（每张照片已经用某种特征提取器提取了特征，形成一组向量），让模型在一组狗狗照片内部进行自注意力计算，以增强每张照片的特征表示。

假设我们有三张狗狗的照片，每张照片都已经通过某个特征提取器（如CNN）提取了特征向量，我们将这三张照片的特征向量作为输入序列。我们的目标是通过自注意力机制，让每张照片的特征都能够考虑到其他照片的特征，从而更好地表示每张照片中狗狗种类的特征。（例如，如果三张照片都是金毛，那么每张照片的特征都会强化金毛的特征）。

具体步骤：

输入序列：三张照片的特征向量，假设每个特征向量的维度是512（即d_model=512）。

照片1: 金毛A（金色长毛，微笑表情）

照片2: 哈士奇（蓝眼立耳，黑白毛色）

照片3: 金毛B（金色长毛，张嘴吐舌）

# 3张照片的原始特征（每张512维）
photo_features = [
    # 照片1: 金毛A
    [0.9, 0.8, 0.2, 0.7, 0.1, ...],  # 金色=0.9, 长毛=0.8, 立耳=0.2, 微笑=0.7, 背景=0.1...

    # 照片2: 哈士奇  
    [0.1, 0.3, 0.9, 0.3, 0.8, ...],  # 金色=0.1, 长毛=0.3, 立耳=0.9, 微笑=0.3, 背景=0.8...

    # 照片3: 金毛B
    [0.8, 0.9, 0.1, 0.6, 0.2, ...]   # 金色=0.8, 长毛=0.9, 立耳=0.1, 微笑=0.6, 背景=0.2...
]
# 形状: [3, 512] - 3张照片，每张512维特征

我们使用单头自注意力（为了简单，我们先不考虑多头）。

我们有三组权重矩阵：W_Q, W_K, W_V，它们的形状都是[512, 64]（这里我们假设d_k=d_v=64）。

在多头注意力中，通常将d_model分割成h个头，每个头的维度为d_k = d_v = d_model / h。如果h=8，那么d_k = d_v = 512/8=64。这个64是预先设定的超参数。但是，实际上d_k和d_v可以是任意值，并不一定要等于d_model/h。然而，在标准的Transformer模型中，为了计算方便，通常令d_k = d_v = d_model / h，这样每个头的输出拼接起来正好是d_model维。这样设计的好处是，多头注意力的输入和输出维度保持一致，便于残差连接。

W_Q = [[0.5, -0.2], [0.1, 0.3], [0.4, 0.1], [-0.1, 0.2]]
W_K = [[0.2, 0.1], [0.3, -0.1], [0.1, 0.2], [0.4, 0.1]]
W_V = [[0.1, 0.3], [-0.2, 0.4], [0.2, -0.1], [0.1, 0.2]]

过程：

对于每张照片，我们通过权重矩阵生成对应的Q、K、V向量。

对于照片1：

Q1 = 照片1特征 * W_Q

K1 = 照片1特征 * W_K

V1 = 照片1特征*W_V

同样得到照片2和照片3的Q2、K2、V2和Q3、K3、V3。

然后，我们以照片1为例，计算照片1的注意力输出。

Q1 = [0.9, 0.2, 0.8, 0.1] * W_Q = [0.9*0.5+0.2*0.1+0.8*0.4+0.1*(-0.1), 0.9*(-0.2)+0.2*0.3+0.8*0.1+0.1*0.2] = [0.45+0.02+0.32-0.01, -0.18+0.06+0.08+0.02] = [0.78, -0.02]

计算注意力分数（以照片1为例）：

分数1 = Q1·K1 = 0.78*0.2 + (-0.02)*0.1 = 0.156 - 0.002 = 0.154
分数2 = Q1·K2 = 0.78*0.3 + (-0.02)*(-0.1) = 0.234 + 0.002 = 0.236
分数3 = Q1·K3 = 0.78*0.1 + (-0.02)*0.2 = 0.078 - 0.004 = 0.074

计算照片1的Q1与所有照片的K向量的点积（包括自己的K1）得到三个分数。

自注意力计算（金毛A的视角）

# 用同一组照片生成Q、K、V（自注意力的核心）
Q = photo_features * W_Q  # 所有照片的查询向量
K = photo_features * W_K  # 所有照片的键向量  
V = photo_features * W_V  # 所有照片的值向量
# 现在我们关注金毛A（照片1）
Q1 = Q[0]  # 金毛A的查询向量
K_all = K  # 所有照片的键向量（包括自己）
# 计算相似度（注意力分数）
# 金毛A问："我应该关注哪些照片的特征来更好地表示自己？"
scores = [
    Q1 · K[0],  # 与自己的相似度
    Q1 · K[1],  # 与哈士奇的相似度
    Q1 · K[2]   # 与金毛B的相似度
]
# 假设得到：
scores = [0.7, 0.1, 0.8]  
# 解释：
# - 与自己的相似度: 0.7
# - 与哈士奇的相似度: 0.1（差异大）
# - 与金毛B的相似度: 0.8（相似度高）

将这三个分数进行softmax归一化，得到三个权重值。

exp(0.154)=1.166, exp(0.236)=1.266, exp(0.074)=1.077

总和=1.166+1.266+1.077=3.509

权重1=1.166/3.509≈0.332

权重2=1.266/3.509≈0.361

权重3=1.077/3.509≈0.307

Softmax得到权重

# 转换为权重（和为1）
weights = softmax([0.7, 0.1, 0.8]) = [0.30, 0.05, 0.65]
# 金毛A的注意力分配：
# - 30%关注自己的特征
# - 5%关注哈士奇的特征（几乎忽略）
# - 65%关注金毛B的特征（重点关注）

用这三个权重值对对应的V向量进行加权求和，得到照片1的注意力输出。

同样，对照片2和照片3进行同样的操作。

加权聚合V得到新特征

# 加权求和所有照片的值向量
new_feature_金毛A = 0.30×V[0] + 0.05×V[1] + 0.65×V[2]
# 效果：金毛A的新特征 =
# - 30%自己的原始特征
# - 5%哈士奇的特征（微弱影响）
# - 65%金毛B的特征（强影响）

输出1 = 权重1*V1 + 权重2*V2 + 权重3*V3

V1 = [0.9, 0.2, 0.8, 0.1]*W_V = [0.9*0.1+0.2*(-0.2)+0.8*0.2+0.1*0.1, 0.9*0.3+0.2*0.4+0.8*(-0.1)+0.1*0.2] = [0.09-0.04+0.16+0.01, 0.27+0.08-0.08+0.02] = [0.22, 0.29]

同样计算V2和V3，然后加权求和。加权求和的输出是：经过上下文信息增强后的新特征表示，通常称为上下文向量（Context Vector）或注意力输出（Attention Output）。

对于金毛A的加权求和输出：

# 输入：金毛A的原始特征
原始_金毛A = [金色:0.9, 长毛:0.8, 微笑:0.7, ...]
# 经过自注意力加权求和后：
新_金毛A = 0.30×V_金毛A + 0.05×V_哈士奇 + 0.65×V_金毛B
# 得到的输出（假设简化）：
新_金毛A = [金色:0.86, 长毛:0.88, 微笑:0.65, ...]
# 变化：金色和长毛特征增强了（从金毛B学到了），微笑特征可能略有变化

这个输出的实际内容为：

输出 = [
    # 维度1：品种特征（强化了）
    金毛特征强度: 0.86  (原来是0.90，但更"标准"了)

    # 维度2：毛长特征（强化了）  
    长毛强度: 0.88  (原来是0.80，从金毛B学到了更长的毛)

    # 维度3：表情特征（可能减弱）
    微笑强度: 0.65  (原来是0.70，因为金毛B在吐舌)

    # 维度4：从金毛B学到的特征
    吐舌特征: 0.12  (原来没有，从金毛B获得)

    # 维度5：背景特征（被抑制）
    背景干扰: 0.05  (原来可能0.10，注意力机制抑制了背景)

    ... 更多特征
]

其实经过公式的运算后，输出是一个加权后的 Value 向量，也是一个多维矩阵，包含了词汇的上下文关系语义信息。

对于分类任务：输出特征更有利于区分品种

对于检索任务：输出特征更有利于匹配查询

对于生成任务：输出特征包含更丰富的上下文信息。

前面我们说了，注意力机制的流程是：

• Query 与 Key 相乘 → 得到注意力分数；
• 用这个分数对 Value 进行加权求和 → 得到输出。

所以，最终的输出其实就是一个融合了上下文信息的 Value 向量。这就是为什么 Transformer 能够捕捉长距离依赖关系的原因：它可以让某个词的表示受到远距离词的影响。

一个融合了上下文信息的新向量，表示当前词在特定上下文中的意义。

02、交叉注意力下的QKV机制

我们通过自注意力机制让每张照片都去“注意”序列中的其他照片，从而更新每张照片的表示。所以，自注意力中的查询、键、值都是来自同一组输入。

我们可以例子调整一下，假设我们有一组狗的照片（每张照片已经用某种特征提取器提取了特征，形成一组向量），然后我们有一个查询（比如查询“金毛狗”的特征向量），我们想要从这组照片中找到与查询最相关的照片。这实际上是一个检索问题，可以用注意力机制来理解，但注意，这不再是自注意力，而是交叉注意力（cross-attention）。在交叉注意力中，查询来自一个序列（比如用户查询），而键和值来自另一个序列（比如狗的照片特征）。

在自注意力中，每个元素（一张狗的照片）都会生成Q、K、V。那么，对于一张照片，它的查询向量可以理解为这张照片的“疑问”：它想知道序列中哪些照片与它相关。键向量可以理解为每张照片的“标识”，用于被查询匹配。值向量是每张照片的实际内容。

但是，交叉注意力有一个明确的用户查询（金毛狗），这更像是将用户查询作为Q，而狗的照片特征作为K和V。这就是交叉注意力。

在交叉注意力中，Q来自一个序列（称为查询序列），而K和V来自另一个序列（称为源序列）。比如，在图像描述生成中，我们可能用图像特征作为K和V，用文本的隐藏状态作为Q。在你的例子中，用户查询“金毛狗”可以作为一个查询向量（假设我们已经将文本“金毛狗”编码为一个向量），而狗的照片特征作为K和V。

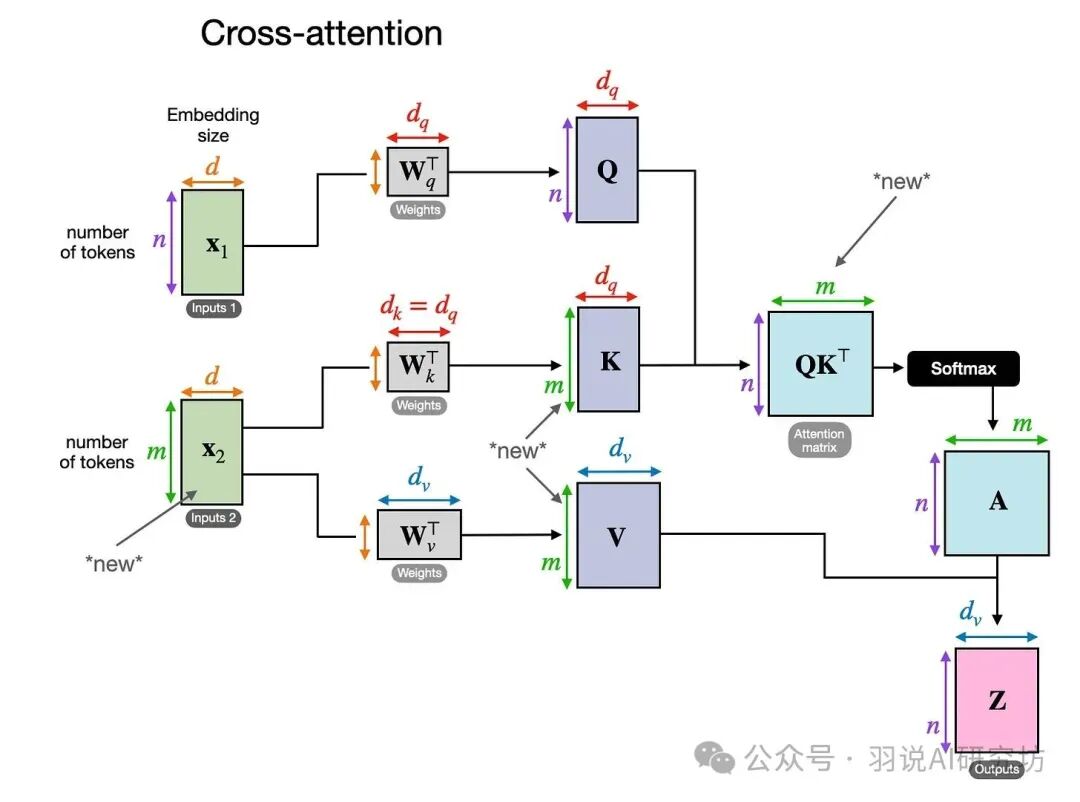
那么，注意力分数可以理解为用户查询向量与每张狗照片的键向量的相似度，分数越高，表示越相关。然后我们用这个相似度作为权重，对狗照片的值向量进行加权求和，得到一个加权后的特征，这个特征可以用于后续的匹配或分类。

请注意，在交叉注意力机制中，两个输入X1序列和X2可以有不同元素的数量。然而，它们的嵌入维度必须匹配。如果我们设置X1=X2，这等同于自注意力机制。

QKV的权重矩阵W

在Transformer的注意力机制中，Q（查询）、K（键）、V不是凭空生成的，而是通过“输入向量 × 对应权重矩阵” 得到的。

先明确两个基础维度（日常常用设置，记熟不混淆）：

d_model：输入向量的维度（即“词嵌入+位置编码”后每个词的向量长度），常用值为 512；

d_k：Q和K的维度（V的维度通常和d_k相同），常用值为 64（选64是为了平衡计算效率和信息保留，避免维度太高导致计算变慢）。

权重矩阵的核心功能：把d_model=512维的输入向量，“转换压缩”成d_k=64维的Q、K、V向量——既保留输入的关键语义/位置信息，又降低后续注意力计算的复杂度。

权重矩阵是线性变换的参数，它们的内容是实数矩阵，通过随机初始化然后梯度下降优化得到，通过梯度下降法不断调整，以最小化损失函数。权重矩阵中的每个参数w_ij都会在每次迭代（或每个批次）中根据梯度进行更新，直到模型收敛（或达到预定的训练轮数）。

单头注意力是最基础的场景（只有1组Q、K、V权重矩阵，分别叫W_Q、W_K、W_V），重点看“维度结构”和“实际计算逻辑”。

1. 权重矩阵的固定维度

不管是W_Q、W_K还是W_V，维度都完全相同，遵循“输入维度 × 输出维度”的规则： 权重矩阵维度 = d_model × d_k → 512 × 64

• 行：对应输入向量的每个维度（512行 → 对应输入向量的512个数字）；
• 列：对应Q/K/V的每个维度（64列 → 对应Q/K/V向量的64个数字）。

2. 用“简化示例”看具体结构（降低维度，更易理解）

为了直观，把d_model简化为4（输入向量是4维），d_k简化为2（Q/K/V是2维），此时W_Q的结构如下（W_K、W_V结构完全一样，只是里面的数字不同）：

关键说明：

• 表中的w_ij（比如w₁₁、w₁₂）：是模型在训练过程中“慢慢学出来的数字”——初始是随机值，训练时会根据任务（比如翻译、文本理解）不断调整，直到Q/K/V能准确计算出“词与词的关联度”；
• 如何得到Q向量？：输入向量（比如[x₁, x₂, x₃, x₄]）和W_Q做矩阵乘法，计算过程如下： Q的第1个数字 = x₁×w₁₁ + x₂×w₂₁ + x₃×w₃₁ + x₄×w₄₁ Q的第2个数字 = x₁×w₁₂ + x₂×w₂₂ + x₃×w₃₂ + x₄×w₄₂ 最终得到2维的Q向量（对应简化后的d_k=2）。

核心总结：Q/K/V权重矩阵的4个关键特征

1. 维度固定：由d_model（输入维度）和d_k（Q/K维度）决定——单头是d_model×d_k，多头是拆成h组d_model×(d_k/h)，维度不会随便变；
2. 数值动态：没有“固定不变的样子”（比如固定的数字），初始是随机值，训练时会根据任务不断优化，最终目的是让Q/K/V能准确捕捉“词与词的关联”；
3. 结构相同，数值不同：W_Q、W_K、W_V的维度完全一样，但里面的w_ij数值不同——因为它们的作用不同（Q负责“查关联”，K负责“被查询”，V负责“提供信息”），需要学习不同的转换规则；
4. “转换器”就是本质注意力机制能高效工作的基础。就是：核心作用是把高维输入向量（512维）转换成适合注意力计算的低维向量（64维），既保留关键信息，又降低计算量，

附：代码视角（帮助理解，可选）

要是后续看代码构建（比如用Python的PyTorch框架），Q/K/V权重矩阵会用“线性层”定义，本质和大家讲的维度一致：

# 定义d_model=512，d_k=64
import torch.nn as nn
# W_Q、W_K、W_V分别对应Q、K、V的权重矩阵（线性层的权重就是我们讲的W_Q/W_K/W_V）
W_Q = nn.Linear(in_features=512, out_features=64)  # 维度512×64
W_K = nn.Linear(in_features=512, out_features=64)
W_V = nn.Linear(in_features=512, out_features=64)
# 输入向量（假设batch_size=1，句子长度=1，即单个词的输入向量）
input_vec = torch.randn(1, 1, 512)  # 形状：(batch, 句子长度, d_model)
# 生成Q、K、V
Q = W_Q(input_vec)  # Q的形状：(1,1,64)，对应d_k=64
K = W_K(input_vec)
V = W_V(input_vec)