组合优化（一）：换手率和alpha模型

新开一个系列写写组合优化的相关内容，主要以分享看到的各种研究和思考为主，偏理论。

第一篇写写换手率，换手直接关系调仓成本，对组合绩效有重要影响。本篇主要参考自quantitative equity portfolio management

01

固定权重组合的换手

换手率的定义为前后两期的权重变化比例

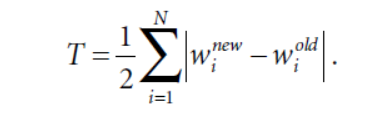
对于一个每期权重固定的组合，换手完全由于每期权重漂移导致，这里权重漂移意思是期初设定权重后，权重会随着股价的变动而变化，因此每一期需要进行再平衡把权重调整到固定值。

两期的权重变化可以表示为

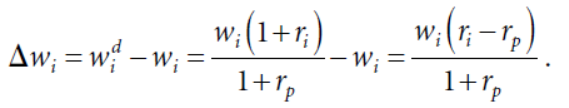
对应的换手为

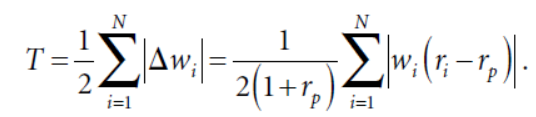
更进一步，假设收益服从正态分布

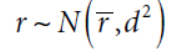
换手可以近似为

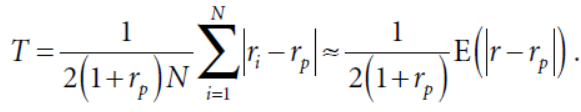
如果是等权重的组合，还可以继续化简

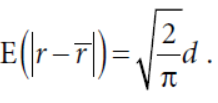
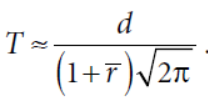
什么意思呢，对于等权重的组合，理论上换手仅和组合收益的一二阶矩相关，波动率越高，换手越高，收益均值越高，换手越低，和直觉也相符。

对于非等权的组合，如果个股间相关性很低的话，换手可以简化为

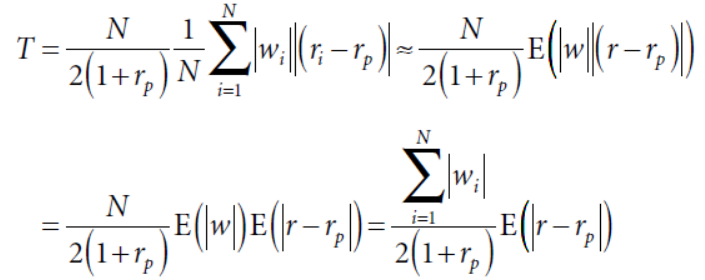
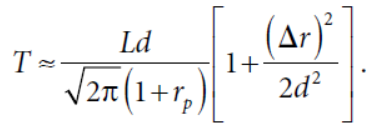
换手取决于收益的离散度，离散度越高，换手越高。

02

预期变动带来的换手

前面分析的是权重固定的组合，对于根据模型进行权重调整的组合，模型结果变动导致的权重变动也会带来换手

公式推导就略了，换手可以表示成预期变动的函数，F表示模型的预测值

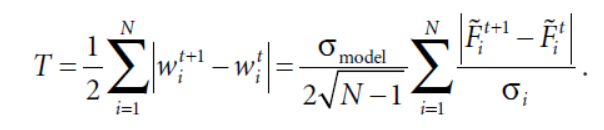
同样的，假设每期的预测都是正太分布，前后两期的相关系数是ρ，T可以近似为

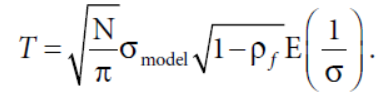
这个就和我们常见的组合优化模型靠的比较近了。σmodel表示跟踪误差，σ表示股票的特质风险，也就是说

跟踪误差越大，股票数N约大，预测的自相关系数越小，股票平均特质风险越低，组合整体换手越高。

因此在主动控制换手外，控制跟踪误差，持股数，以及模型预测的自相关性，也可以一定程度上控制换手

03

因子自相关与换手

上面分析表明，模型的自相关性越高，换手越低，我们一般的多因子模型都是由多个类别低相关的因子合成而来，多因子模型的换手和每个单因子的自相关性都相关。

这边对一个简单情况进行测算，假设一个模型有两个因子F1、F2构成

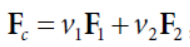
模型的自相关性定义如下

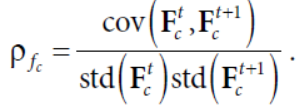
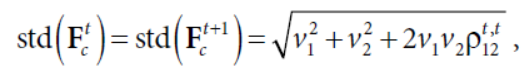
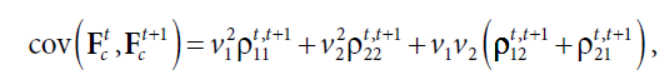
ρij是因子的互相关性,ρii是因子的自相关系数，化简一下

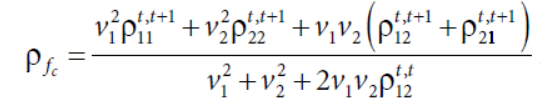
因此，合成因子的自相关性取决于两个单因子的自相关性、截面互相关性，和直觉也相符。而moving average可以增加因子的自相关性，从而降低组合的换手。

04

交易成本

组合优化时需要考虑交易成本，从交易成本来源出发，有两类交易成本：固定成本和可变成本。

固定成本包括交易费用以及买卖价差，这两种都是成交量的线性函数，因此固定成本可以建模为

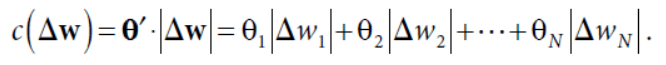
对于可变成本，包括市场冲击和机会成本，市场冲击指投资者交易导致的价格变动，导致成本上升。这部分是非线性的，没有固定的形式，可以用二次模型近似表示

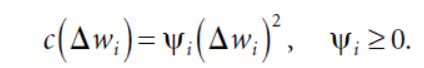
并且二次模型更容易去优化求解。

05

单个资产的优化

单个资产的线性成本下进行组合优化

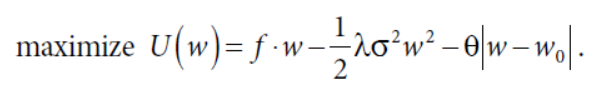
求导之后可以求出最优值

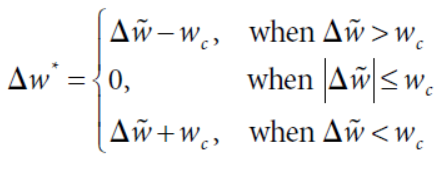
其中，

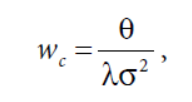
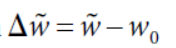
过程略过，详见原文。权重变化的图像长这样

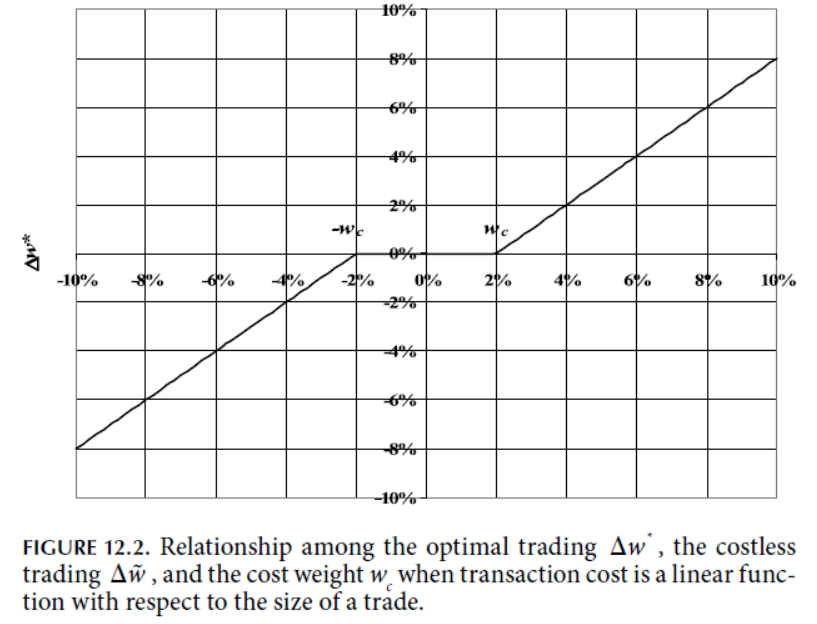
θ是换手惩罚系数，θ越高，wc越大，调仓的临界值越高，中间不调仓的部分越宽。对theta遍历，最优权重如下，这里假设期初的权重是50%，随着θ增大，交易量会下降到0。

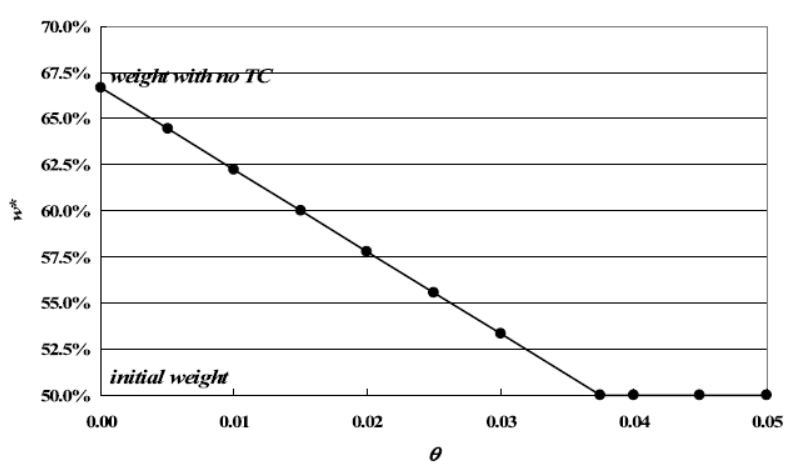
如果是二次成本

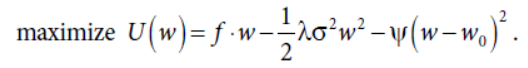
公式推导略过，

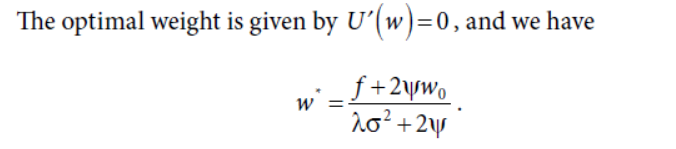
这种情况下的权重随换手惩罚系数的变动如下图

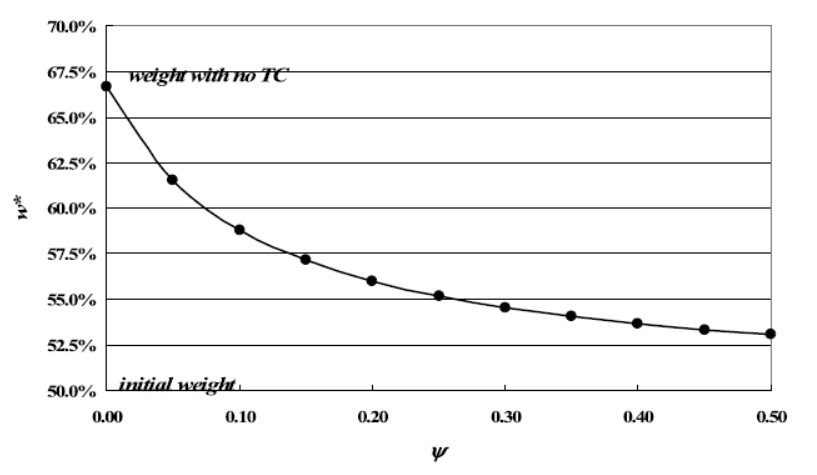
对比线性和二次的惩罚项，可以明显看出，二次惩罚下，无论惩罚系数多大，始终都会有交易存在，无穷大的时候，接近于期初权重。

06

多资产优化

多资产时候，w是一个向量，二次换手惩罚下

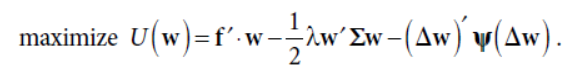
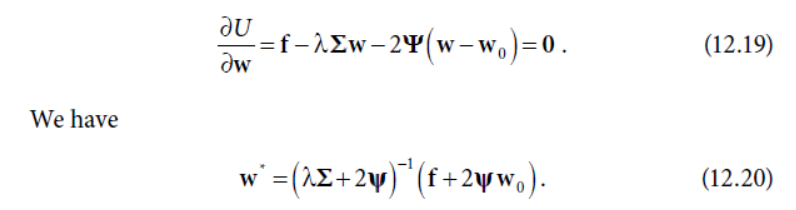
如果拉长看很多期

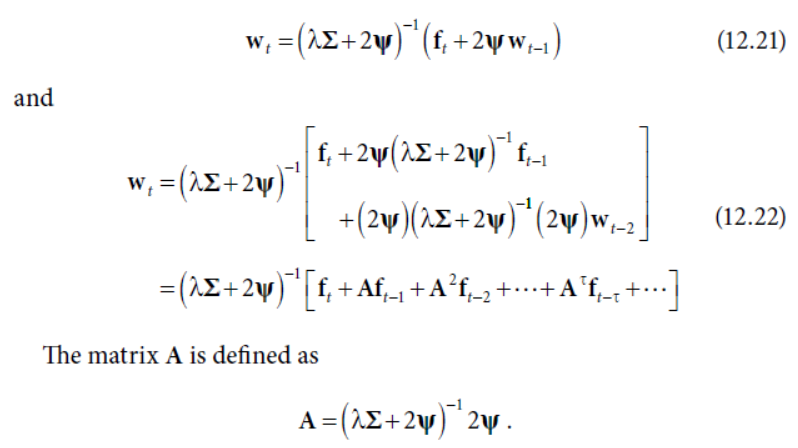
这样可以把单期模型转化成一个多期模型

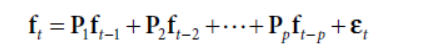
多期里，对两类信息，一类高IC但高衰减的快信息，一类低IC但低衰减慢信息，考虑交易成本的情况下，加大慢信息的权重，降低快信息的权重，可以增加多期的IR。

写在最后

第一篇以换手开篇，原因在于换手在组合优化里有着重要的作用，不考虑成本的组合可以直接最大化组合alpha来获取，考虑换手后，信息会被分成文末说的两类，一类高换手高alpha，一类低换手低alpha，等权来使用必然不是最优的方法。

另一方面，我们也希望能有低换手高alpha的信息，但这个比较理想，比较现实的是通过模型处理来降低换手的同时较少的alpha，文中关于自相关的分析主要是想说明这一点。