生成图像动力学:Generative Image Dynamics
生成图像动力学:Generative Image Dynamics
用户1324186
发布于 2023-09-24 19:27:11
发布于 2023-09-24 19:27:11
作者: Zhengqi Li 等 论文题目:Generative Image Dynamics 论文链接:https://generative-dynamics.github.io/static/pdfs/GenerativeImageDynamics.pdf 内容整理:汪奕文 本文提出一种对场景动态的图像空间先验建模的方法。该先验是从包含自然振荡运动的真实视频序列中提取的运动轨迹集合中学习的。给定一幅图像,所提出的训练模型使用频率协同扩散采样过程来预测频域中每个像素的长期运动表示,称为神经随机运动纹理。与基于图像的渲染模块一起,这些轨迹可用于许多下游应用,例如将静态图像转换为无缝循环的动态视频,或允许用户与真实图片中的物体进行交互。
引言
生成模型,特别是条件扩散模型,使我们能够模拟高度丰富和复杂的分布,甚至是以文本为条件的真实图像分布。这种能力使许多以前不可能实现的应用成为可能,例如以文本为条件生成任意、多样且逼真的图像内容。在这些图像模型取得成功之后,最近的研究表明,其他领域的建模,如视频和三维几何领域,也同样适用于下游应用。
在这篇文章中,作者探讨了图像空间场景运动(即单张图像中所有像素的运动)的生成先验建模。该模型是根据从大量真实视频序列中自动提取的运动轨迹进行训练的。在输入图像的条件下,模型会预测出神经随机运动纹理,用于描述每个像素未来的运动轨迹。作者将研究范围限定在具有自然摆动的真实世界场景,如随风飘动的树木和花朵,因此选择傅里叶级数作为基函数。作者使用扩散模型来预测神经随机运动纹理,该模型每次只生成一个频率系数,但会在不同频段之间协调这些预测。由此产生的频率空间纹理可以转化为密集的长距离像素运动轨迹,这些轨迹可用于合成未来帧,将静态图像转化为逼真的动画。
与原始 RGB 像素先验相比,运动先验能捕捉到更基本、更低维的底层结构,从而有效解释像素的变化。因此,与之前通过 raw 视频合成来生成图像动画的方法相比,本文的运动表示法能带来更连贯的长时间生成和更精细的动画控制。该生成运动表示法可以用于许多下游应用,如生成无缝循环视频、编辑生成的运动,以及实现交互式动态图像。
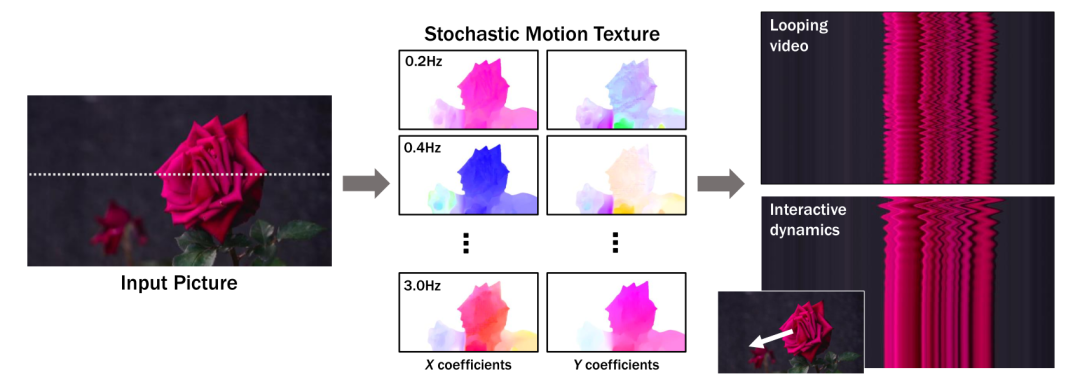
图1
整体框架
对于给定的单张图像
, 目标是生成长度为
的视频
,并且包含了树木、花朵或微风中摆动的蜡烛火焰等的动态特征。
整体框架由两个模块组成:运动预测模块和图像渲染模块。
首先使用 LDM 来预测输入图像
的神经随机运动纹理
。随机运动纹理是输入图像中每像素运动轨迹的频率表示。之后,利用离散傅立叶逆变换将预测的随机运动纹理转换为运动位移场
序列。运动场反过来用于确定每个输入像素在未来时间的位置。
基于预测的运动场,渲染模块使用基于图像的渲染技术对输入的 RGB 图像进行动画处理,对输入图像中的编码特征进行拼接,并通过图像合成网络将这些拼接特征解码为输出帧。
神经随机运动纹理
运动纹理
运动纹理定义了一系列随时间变化的二维位移图
。其中输入图像
中每个像素坐标
处的二维位移向量
定义了该像素在未来时刻
的位置。要生成
时刻的未来帧,可以使用相应的位移图
对
中的像素进行拼接,从而生成前向 warp 图像
。
随机运动纹理
许多自然运动,尤其是振荡运动,都可以被描述为少量谐波振荡的叠加,这些谐波振荡具有不同的频率、振幅和相位。在时域中采用运动纹理意味着要预测
个 2D 位移场,才能生成具有
个帧的视频。为了避免预测庞大的输出表示,许多先前的动画制作方法要么自动生成视频帧,要么通过额外的时间嵌入独立预测每个未来输出帧。然而,这两种方法都不能确保生成的视频帧在时间上的长期一致性,而且都会生成随时间漂移或偏离的视频。
为解决上述问题,作者提出了在频域中表示输入场景每个像素的运动纹理,并将运动预测问题表述为多模态图像到图像的转换任务。采用 LDM 来生成随机运动纹理,它由
通道 2D 运动频谱图组成,其中 K<<T 是建模频率的数量。并在每个频率上采用四个标量来表示 x 和 y 方向的复傅立叶系数。
未来时刻像素的运动轨迹
及其频域运动谱
可以通过傅里叶变换相互转换。
先前的实时动画研究发现,大多数自然振荡运动主要由低频成分组成。为了验证这一假设,作者计算了从 1000 个随机取样的 5 秒真实视频片段中提取的运动的平均功率谱。运动的功率谱随着频率的增加呈指数下降。在实践中,前
个傅立叶系数足以真实再现视频和场景中的原始自然运动。
基于扩散模型的运动预测
选择 LDM 作为运动预测模块的pipeline。LDM 由两个主要模块组成。变分自编码器 (VAE),通过编码器
将输入图像压缩到隐空间,然后通过解码器
从隐空间特征重建输入图像。基于 U-Net 的扩散模型从高斯随机噪声开始对隐空间特征迭代去噪。
训练不是针对输入图像,而是针对真实视频序列中的随机运动纹理,对其进行编码,然后进行
步扩散,以生成噪声隐空间特征
。通过迭代估计噪声
,训练二维 U-Net 对隐空间特征去噪。LDM 的训练损失为
其中,
是任何条件信号的嵌入。在本文中,条件嵌入
是训练视频序列的第一帧
。
频率自适应归一
随机运动纹理在不同频率下具有特定的分布特征。由于扩散模型要求输出值介于 0 和 1 之间,以保证能够稳定地训练和去噪,先将从真实视频中提取的
系数进行归一化处理。
由于扩散模型要求输出值介于 0 和 1 之间,以便进行稳定的训练和去噪,因此我们必须先将从真实视频中提取的
系数归一化,然后再将其用于训练。如果直接根据图像的宽度和高度将
系数缩放至
,那么几乎所有的高频系数都会趋近于零,在这种数据上训练的模型可能会生成不准确的运动。
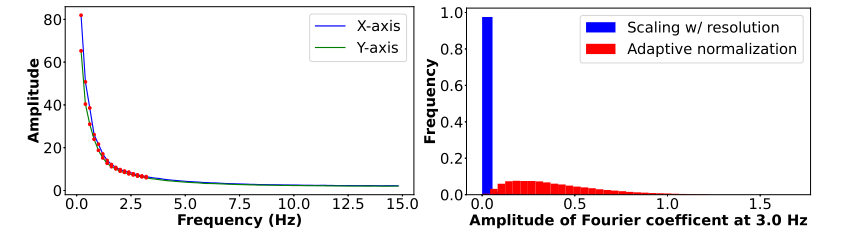
图2 左:真实视频数据集的运动功率谱 右:3Hz(K = 16)时傅里叶项振幅的直方图
为了解决这个问题,作者采用了一种简单而有效的频率自适应归一化技术。首先根据从训练集中计算出的统计数据,对每个频率的傅立叶系数进行独立归一化。在每个频率
上,计算所有输入样本中傅立叶系数幅度的
百分位数,并将该值作为傅立叶系数的第 97 个百分位数,并使用该值作为每个频率的缩放因子
。之后,对缩放后的傅立叶系数进行幂变换,使其远离极小或极大值。随机运动纹理
在频率
处的最终系数值计算如下
频率协同去噪
预测具有
个频带的随机运动纹理
的直接方法是通过 U-Net 输出一个包含
个通道的张量。然而,直接训练一个模型来生成如此大量的通道数往往会产生过度平滑和不准确的输出。另一种方法是通过向 LDM 注入额外的频率嵌入,在每个频率上独立预测运动频谱图,但这会导致频域上的预测不相关,从而导致不切实际的运动。
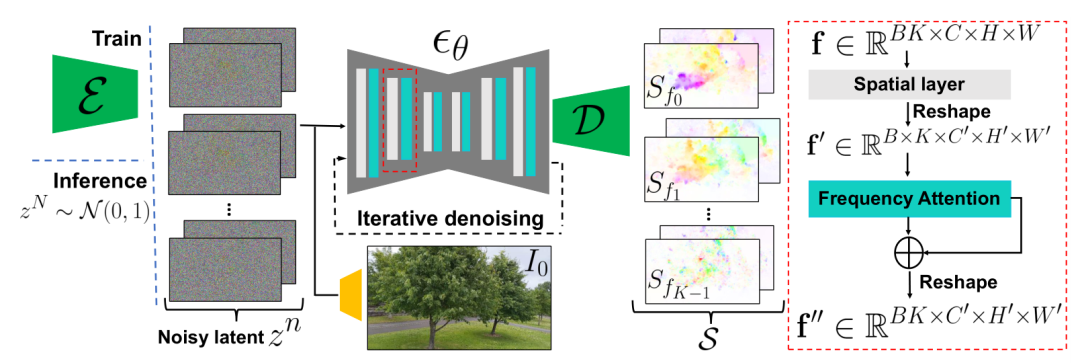
图3 基于扩散模型的运动预测
因此,本文提出了一种频率协同去噪方法。对于给定的输入图像
,首先训练一个 LDM
来预测随机运动纹理
,用四个通道来表示每个频率
。然后,冻结该 LDM 模型的参数
,并引入注意力层,在
个频段上与
的 2D Spatial 层交错。
具体来说,对于batchsize 为
的输入图像,
的 2D Spatial 层将通道大小为
的
个噪声潜在特征视为独立样本,其形状为
。然后,交叉注意层将这些特征解释为跨频率的连续特征,并 reshape 为
。频率注意力层用于协调所有频率通道的预训练运动隐空间特征,以保证生成连贯的随机运动纹理。
图像渲染
首先,通过逆 FFT 推导出运动轨迹场
,这确定了每个输入像素在未来时刻的位置。之后,采用基于深度图像的渲染技术,并与预测的运动场
进行 splatting,以获得前向 warping 的
。
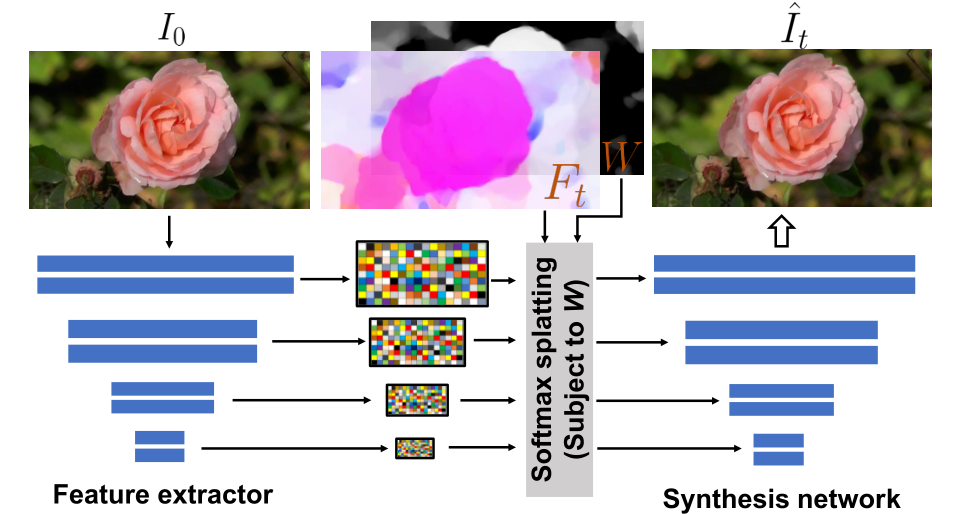
图4 图像渲染模块
由于前向 warping 会导致空洞,而多个源像素可以映射到相同的 2D 输出位置,因此本文采用了特征金字塔 softmax splatting 策略。具体来说,我们通过特征提取器网络编码
,以产生一个多尺度特征图
。
对于每个尺度
的特征图
,根据
的分辨率调整预测的 2D 运动场
的大小和尺度。之后,计算每个像素的权重
,并将其作为预测运动轨迹场的平均幅度。也就是说,假设大运动对应于前景物体的移动,小运动或零运动对应于背景物体的移动。
得到了运动场
和权重
后,将 softmax splatting 应用于每个尺度的特征图,以生成 warped 特征
。然后将特征
注入到图像合成解码器网络的中间块中,以生成最终的渲染图像
。
使用从真实视频中随机抽样的起始帧和目标帧
联合训练特征提取器和合成网络。使用从
到
的估计流场来 warp
的隐空间特征,并使用 VGG 感知损失监督
对
的预测。

图5 图像渲染结果 (a)RGB 像素域平均 splatting,(b)可学习权重的 softmax splatting,(c)动作感知特征 splatting
实验
应用场景
图像-视频
首先从输入图像预测神经随机运动纹理,并通过将基于图像的渲染模块应用于随机运动纹理所导出的运动位移场来生成动画,从而实现从单幅静止图像生成动画。
无缝循环视频
本文设计了一种方法,使用在常规非循环视频片段上训练的运动扩散模型,以生成无缝循环视频。受最近关于指导图像编辑的工作的启发,所提出方法是一种运动自指导技术,使用显式循环约束指导运动去噪采样处理。特别是,在推理阶段的每个迭代去噪步骤中,将额外的运动指导信号与标准的无分类器指导结合在一起,约束起始帧和结束帧中每个像素的位置和速度尽可能相似。
单张图像生成交互式动画
从一个振动物体的观察视频中得到的图像空间运动谱近似于该物体的物理振动模态基。模态形状捕获了物体在不同频率下的振荡动态,因此物体振动模态的图像空间投影可以用来模拟物体对用户定义的力(如戳或拉)的响应。作者采用模态分析技术,假设物体的运动可以用一组谐振子的叠加来解释,将物体物理响应的图像空间 2D 运动位移场写成傅立叶谱系数
和每个模拟时间步
的复模态坐标
的加权和。
实施细节
使用 LDM 作为预测随机动作纹理模块的 backbone,其中 VAE 的隐空间维度为 4。使用
损失、多尺度梯度一致性损失和 KL 正则化损失训练 VAE。
为了进行定量评估,作者在大小为
的图像上对 VAE 和 LDM 进行了训练,使用 16 个 Nvidia A100 GPU,大约需要 6 天才能收敛。对于主要的定量和定性结果,使用 DDIM 推理 500 步,并设置
以生成随机运动纹理。在消融性实验中,DDIM 推理步骤运行 200 步,且
。
实验结果
本文的方法和 baseline 方法之间的定量比较。所提出方法在图像和视频合成质量方面明显优于之前的单图像动画 baseline。更低的 FVD 和 DT-FVD 表明所提出方法生成的视频更真实,且在时间上更连贯。
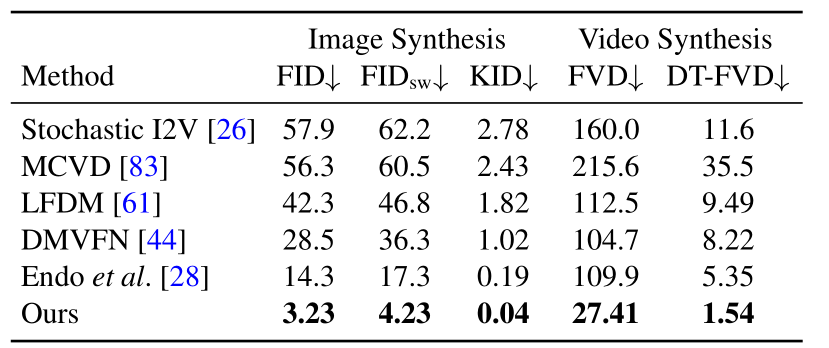
表1
由于所提出的全局随机运动纹理表示,所提出方法生成的视频在时间上更一致,不会随着时间的推移而漂移或退化。
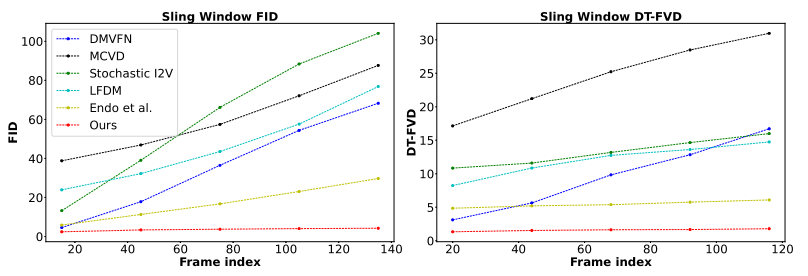
图6 不同方法生成视频的滑动窗口 FID 和滑动窗口 DT-FVD 距离
通过两种方式可视化了由本文方法和 baseline 生成的视频之间的定性比较。首先,展示了生成视频的时空
切片。与其他方法相比,所生成的视频动态更类似于在相应的真实参考视频中观察到的运动模式。

图7 视频的时空 X-t 切片
与其他方法相比,本文的方法生成的帧中伪影和失真更少,相应的 2D 运动场与从相应的真实视频中估计的参考位移场最相似。相比之下,其他方法生成的背景内容更容易发生漂移,或表现出显著的颜色失真或伪影,这表明在生成长时间视频时,baseline 不太稳定。

图8 对生成的未来帧和相应运动场进行视觉比较
本文参与 腾讯云自媒体同步曝光计划,分享自微信公众号。
原始发表:2023-09-24 09:50,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

