时间序列预测的零样本学习：TimeGPT vs. TiDE

在本文中，我们将讨论一个通用的预训练模型能否解决预测任务的范式转变。我们通过使用TimeGPT进行零样本学习并对模型的性能进行了彻底分析。然后将TimeGPT的性能与TiDE[2]进行比较（TiDE是一种在预测用例中击败了Transformer的简单的多层感知机)。

TimeGPT

TimeGPT [1] 是时间序列预测的第一个基础模型，其特点是能够在不同领域之间进行泛化。它可以在训练阶段之外的数据集上产生精确的预测。

最近围绕用于时间序列预测的研究领域的基础模型正在经历显著增长。最近发布的新方法包括：卡内基梅隆大学（CMU）研究人员开发的“MOMENT” [3]、谷歌的“TimesFM” [4]、摩根士丹利和ServiceNow合作开发的“Lag-Llama” [5]，以及Salesforce的“Moirai” [6]。我们以前也介绍过一些，随后的文章会将其他的模型进行逐个说明。

现在我们回到TimeGPT ，它号称利用迁移学习在零样本推理设置中表现出色。它使用了来自经济学、人口统计学、医疗保健、天气、物联网传感器数据、能源、网络流量、销售、交通和银行等各种领域的大量公开可用数据集，总共达到了1000亿个数据点。

这种广泛多样的领域使模型能够捕捉复杂的模式，例如多个季节性、不同长度的周期和不断演变的趋势。数据集展示了各种噪声水平、异常值、漂移和其他特征。一些数据集由干净的数据组成，具有规律的模式，而另一些则具有意外事件和行为，其中趋势和模式可能随时间波动。这些挑战为模型提供了许多学习的场景，提高了其鲁棒性和泛化能力。

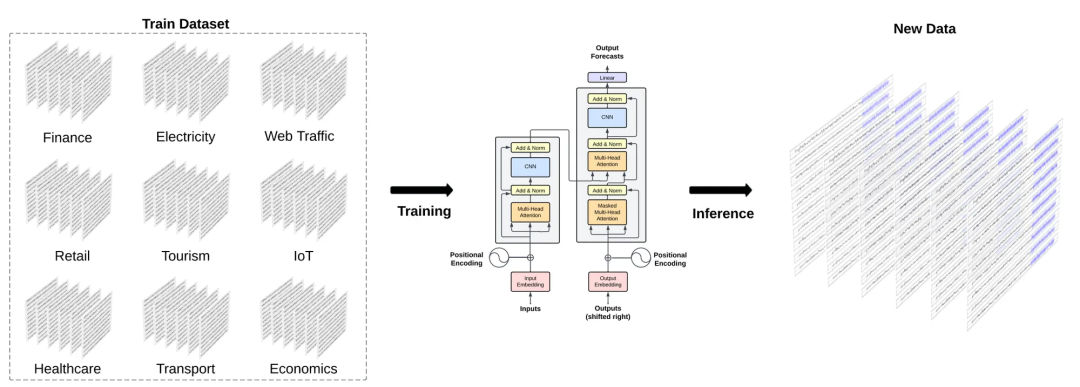
网络架构

TimeGPT 是一个基于变换器的模型，专为时间序列预测而设计，在编码器-解码器架构中加入了自注意力机制。通过利用自注意力机制，它可以动态权衡时间序列中不同点的重要性。

该模型接收历史值窗口（y）和外生协变量（x）作为输入。协变量可包括额外的时间序列数据和/或表示特定事件（如公共节假日）的二进制变量。通过整合本地位置嵌入，这些输入将得到序列信息的补充。这样，模型就能意识到时间依赖性。虽然作者没有明确说明，但我们认为所有输入都是在位置编码后进行串联的，从而产生最终输入，为编码器提供信息。

作者也没有定义位置编码。我们假设他们使用的是基础变压器架构论文[7]中的正弦和余弦函数。这些函数的特点是频率不断变化，但保持与输入数据相同的维度。

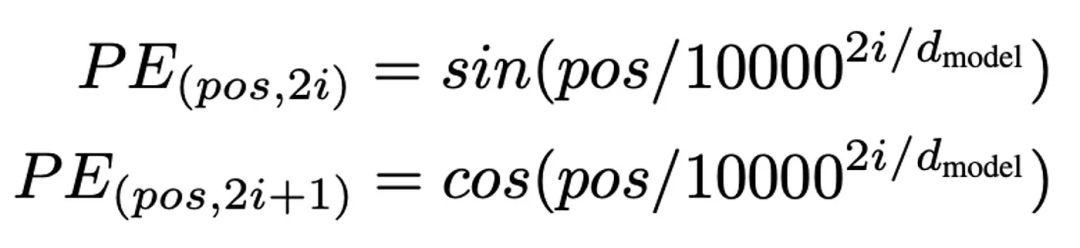
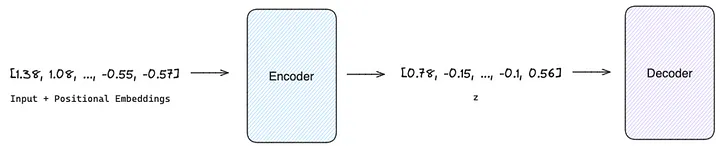
输入矢量经位置编码增强后，被引入编码器。在编码器中，多头注意力层对输入序列中的各种元素进行评估并分配权重，以反映它们的相对重要性。随后，这一表征由一个全连接的前馈网络进行处理。这样就能生成一个能捕捉序列中各元素之间更复杂关系的表征。然后，将输出输入该架构的解码器部分。

除处理编码器的输出外，解码器还以自动回归的方式运行。在生成后续时间步长（i+1）的预测之前，解码器会吸收之前生成的输出。解码器利用注意力机制捕捉编码器生成的隐藏状态与之前生成的输出之间的复杂关系。这种方法使解码器能够有效地将编码器表征中包含的上下文和顺序信息与自身的迭代预测进行综合。

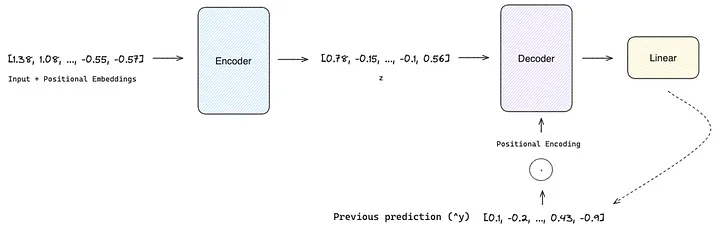
最后，线性层负责将解码器的输出映射到与预测范围（h）长度相同的值向量上。

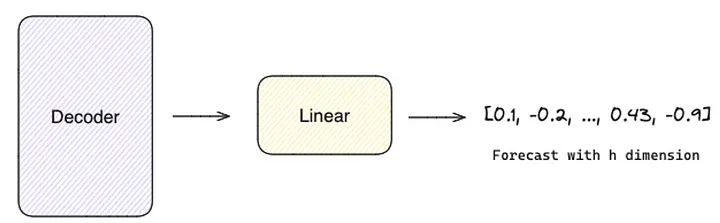
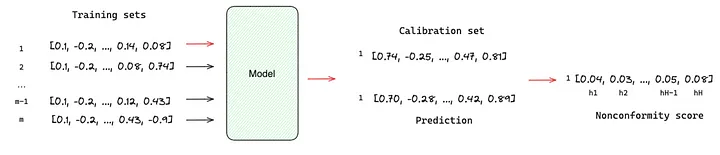
TimeGPT是一个基于transformer的模型，可以生成潜在结果的概率分布，即预测区间的估计。依靠基于历史误差的符合性预测 [8] 来估计预测区间。与传统方法不同，符合性预测不需要分布假设，可以通过以下步骤实现：

1. 创建 M 个训练和校准集；
2. 使用模型对每个校准集进行预测；
3. 对于每个预测的时刻 h，计算模型预测值与校准集内实际结果之间的绝对残差值。这些计算出的残差称为非符合性分数；
4. 我们从每个预测时刻 h 的非符合性分数分布中选择特定的分位数。所选择的分位数决定了预测区间的覆盖水平，较高的分位数会导致更宽的区间。

预测区间由预测值 ± 最终的非符合性分数给出。

TiDE

TiDE 是23年4月谷歌发布的的多变量时间序列模型，可以在预测时段使用静态协变量（例如产品的品牌）和已知或未知的动态协变量（例如产品的价格）来生成准确的预测。与Transformers的复杂架构不同，TiDE 基于一个简单的编码器-解码器架构，并使用了残差连接：

• 编码器负责将时间序列的过去目标值和协变量映射为特征的密集表示。特征投影降低了动态协变量的维度。密集编码器接收特征投影的输出与静态协变量以及过去的值的拼接，并将它们映射成单一的嵌入表示。
• 解码器接收嵌入表示，并将其转换为未来的预测。密集解码器将嵌入表示映射到预测时段每个时间步的向量。然后，时间解码器将密集解码器的输出与该时间步的特征投影相结合，产生预测。
• 残差连接线性地将回溯映射为与预测时段大小相同的向量，将其添加到时间解码器的输出中以产生最终的预测。

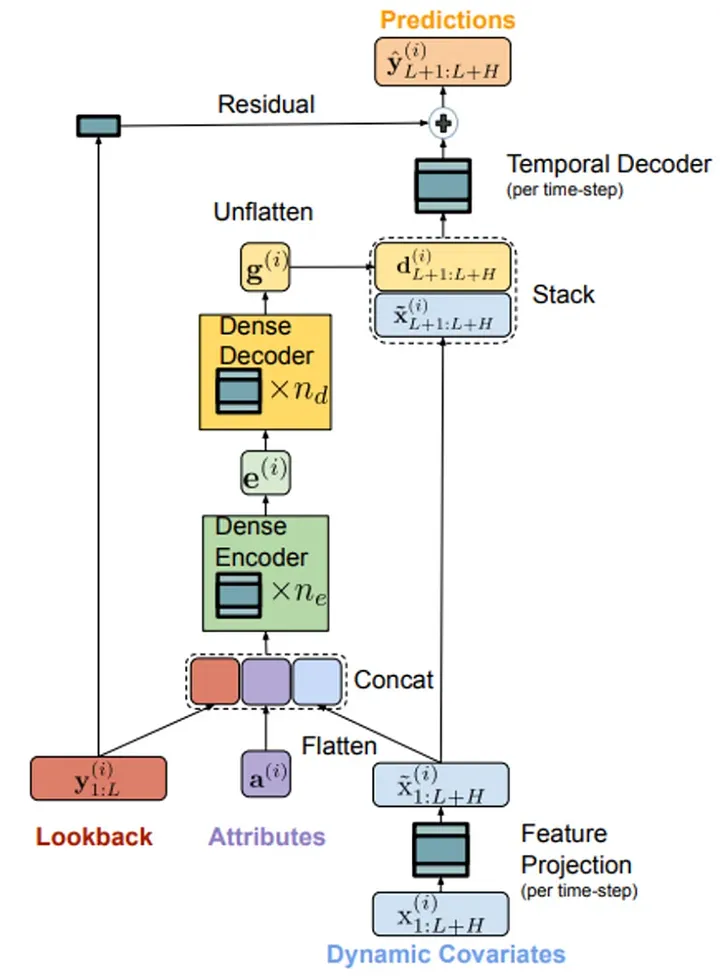
通过这种简单而有效的架构，TiDE能够利用静态和动态协变量生成准确的销售预测。就像之前更早的Dlinear类似，针对特定的任务简单的线性层可以获得更好的结果。

下面我们就要使用TimeGPT和TiDE应用于客户的销售数据（这是一个真实世界的数据集），并对其性能进行比较和分析。

TimeGPT VS TiDE

数据集包含195个唯一的时间序列，每个序列详细说明了美国市场的每周销售数据。除了历史销售数据外，数据集还包含两种类型的营销事件信息。并且合并了公共假日和二元季节性特征来增强数据集。预测范围是16周，也就是说想要预测未来16周的情况。

我们先导入包

 import matplotlib.pyplot as plt
 import os
 import pandas as pd
 import utils
 
 from nixtlats import TimeGPT
 from nixtlats.date_features import CountryHolidays
 from dotenv import load_dotenv
 from sklearn.preprocessing import MinMaxScaler, OrdinalEncoder
 
 load_dotenv()

然后，通过提供TimeGPT令牌来初始化TimeGPT类。

 timegpt = TimeGPT(token = os.environ.get("TIMEGPT_KEY"))
 timegpt.validate_token()

加载数据集时需要保证格式如下：

目标变量应该是数字的，并且没有缺失值；确保从开始日期到结束日期的日期序列中不存在间隙；日期列必须采用Pandas可识别的格式；TimeGPT可以进行数据缩放（归一化等）所以可以跳过这一步；对于预测多个时间序列，需要一个列来唯一地标识每个序列，这将用作预测函数中的参数；外生特征需要一个单独的数据集用于预测时段。

通过上面的介绍，我们可以看到，TimeGPT把最复杂的部分留给了我们，填充缺失值（包括保证时间序列的连续性）是最麻烦的事情。

我们读取自己处理好的数据集

 df = pd.read_csv('data/data.csv', parse_dates=['delivery_week'])

然后添加周和月的二元季节性特征:

 # add week and month to df
 df['week'] = df['delivery_week'].dt.isocalendar().week
 df['month'] = df['delivery_week'].dt.month
 
 # one hot encode week and month
 df = pd.get_dummies(df, columns=['week', 'month'], dtype=int)

截断数据集以供TimeGPT用于预测，剩下作为验证集进行验证。

 # Truncate data frame
 forecast_df = df[df['delivery_week'] < "2023-10-16"]
 
 # Let's use the last x weeks of actuals for the holdout set
 holdout_df = df[(df['delivery_week'] >= "2023-10-16") & (df['delivery_week'] <= "2024-02-05")]

分割数据后，可以将训练数据集和保留数据集输入 forecast() 函数。

需要设置以下参数：

• df- 包含历史数据的数据帧
• time_col- 包含时间信息的列
• target_col- 包含历史数据的列
• X_df- 包含预测范围外生特征的数据帧
• date_features- 允许指定新的外生特征，如美国的公共假期
• h- 确定预测范围
• level- 预测区间（80% 置信度）
• freq- 数据频率，本例中为每周星期一
• id_col- 在多元情景中标识每个时间序列的列
• model- TimeGPT 有两个模型，一个是短期模型，另一个是长期模型。当预测范围内有一个以上的季节性时期时，应使用长期模型。
• add_history- 返回历史数据中的拟合值

 # create list with seasonal exogenous features
 EXOGENOUS_FAETURES = [x for x in df.columns if ('week_' in x) | ('month_' in x)]
 
 timegpt_fcst_ex_vars_df = timegpt.forecast(
    df=forecast_df[['unique_id', 'delivery_week', 'target', 'marketing_events_1', 'marketing_events_2']+EXOGENOUS_FAETURES],
    time_col='delivery_week',
    target_col='target',
    X_df=holdout_df[['unique_id', 'delivery_week', 'marketing_events_1', 'marketing_events_2']+EXOGENOUS_FAETURES],
    date_features=[CountryHolidays(['US'])],
    h=17,
    level=[80],
    freq='W-MON',
    id_col='unique_id',
    model='timegpt-1',
    add_history=True,
    )

API的预测只需要几分钟。它返回数据包含历史数据的拟合值和预测范围的预测值，并且还返回了外生协变量在预测中的重要性。

 timegpt.weights_x.head(10).sort_values(by='weights').plot.barh(x='features', y='weights')
 plt.title('Feature Importance - top 10')
 plt.show()

提取了十个最重要的协变量，这表明营销事件具有最高的重要性。

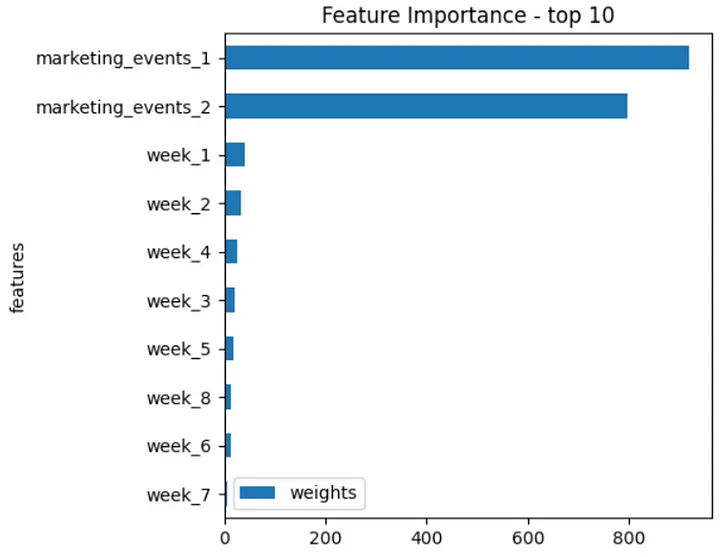
我们设置了add_history=True，所以可以绘制拟合值和预测值。选择了保留数据集中数量最多的六个series 。它们与业务更相关，预测起来可能更容易，模式也更稳定。

# get series ordered by volume in a descending way
series = holdout_df.groupby('unique_id')['target'].sum().reset_index().sort_values(by='target', ascending=False)['unique_id'].tolist()

timegpt.plot(
    forecast_df[['unique_id', 'delivery_week', 'target']], 
    timegpt_fcst_ex_vars_df,
    time_col='delivery_week',
    target_col='target',
    unique_ids=series[:6],
    level=[80], 
)

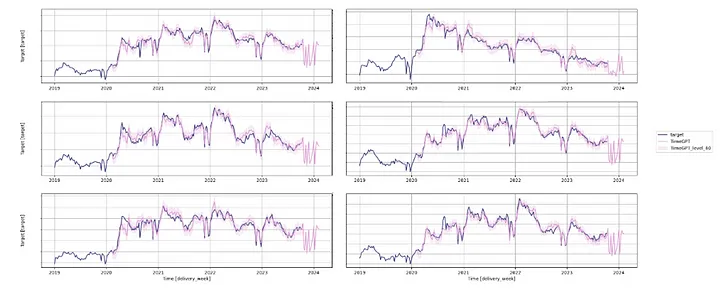
可以看到虽然拟合值与实际值很好地吻合，但预测结果并不一致。它们在大多数序列中显示出一致的模式。

下面我们看看TiDE生成的预测，然后就可以对预测性能指标以进行比较。这里使用平均绝对百分比误差(MAPE)作为比较指标，这样可以防止实际销售量的泄露，又能看到实际的对比结果。

 # load the forecast from TiDE and TimeGPT
 tide_model_df = pd.read_csv('data/tide.csv', parse_dates=['delivery_week'])
 timegpt_fcst_ex_vars_df = pd.read_csv('data/timegpt.csv', parse_dates=['delivery_week'])
 
 # merge data frames with TiDE forecast and actuals
 model_eval_df = pd.merge(holdout_df[['unique_id', 'delivery_week', 'target']], tide_model_df[['unique_id', 'delivery_week', 'forecast']], on=['unique_id', 'delivery_week'], how='inner')
 
 # merge data frames with TimeGPT forecast and actuals
 model_eval_df = pd.merge(model_eval_df, timegpt_fcst_ex_vars_df[['unique_id', 'delivery_week', 'TimeGPT']], on=['unique_id', 'delivery_week'], how='inner')
 
 utils.plot_model_comparison(model_eval_df)

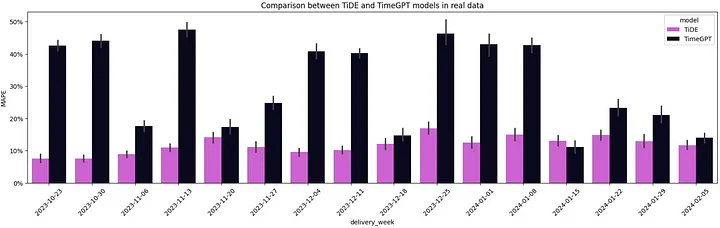
在16周的195个时间序列中，有15周TiDE的平均MAPE低于TimeGPT。TimeGPT的零样本学习能力并没有打败我们的微调模型，并且这个模型是23年4月发布的，到现在已经有将近1年的时间了。

总结

在本文中，我们探讨了时间序列预测的最新创新之一——基础模型的发展。这些模型的目标是为缺乏内部开发SOTA模型所需的专业知识的组织提供对算法的使用。这种方式很有希望，但我们验证结果表明，它仍然无法提供准确的预测，也就是说目前来TimeGPT作为基础模型还是不够好。

另外还需要说明的是这里为了简单对比所以我们没有进行人工的特征工程和使用XGB等提升树的模型进行计算。因为目前来看无论是lightgbm还是xgboost，都是目前时间序列预测的sota：这点可以从时间序列发布的论文中看到，所有论文的结果展示没有和它们进行对比的，而对比对象的都是一些前辈（transformer类的深度学习模型）。

虽然目前来看时间序列的基础模型还不够完善，TimeGPT可以说是一个失败的模型，但是我们也可以看到目前的研究方向也在向时间序列的基础模型而努力。虽然其他领域，如计算机视觉和NLP，基础模型已经获得越来越多的关注并且可以说是成功了，但时间序列预测这个领域还有是有很大的研究前景的。

以下是本文的引用：

[1] Garza, A., & Mergenthaler-Canseco, M. (2023). TimeGPT-1. Retrieved from arXiv:2310.03589. [2] Abhimanyu Das, Weihao Kong, Andrew Leach, Shaan Mathur, Rajat Sen, Rose Yu. (2023) Long-term Forecasting with TiDE: Time-series Dense Encoder. arXiv:2304.08424. [3] Goswami, M., Szafer, K., Choudhry, A., Cai, Y., Li, S., & Dubrawski, A. (2024). MOMENT: A Family of Open Time-series Foundation Models. Retrieved from arXiv:2402.03885 (cs.LG). [4] Das, A., Kong, W., Sen, R., & Zhou, Y. (2024). A decoder-only foundation model for time-series forecasting. Retrieved from arXiv:2310.10688 (cs.CL). [5] Rasul, K., Ashok, A., Williams, A. R., Ghonia, H., Bhagwatkar, R., Khorasani, A., Darvishi Bayazi, M. J., Adamopoulos, G., Riachi, R., Hassen, N., Biloš, M., Garg, S., Schneider, A., Chapados, N., Drouin, A., Zantedeschi, V., Nevmyvaka, Y., & Rish, I. (2024). Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting. Retrieved from arXiv:2310.08278 (cs.LG). [6] Woo, G., Liu, C., Kumar, A., Xiong, C., Savarese, S., & Sahoo, D. (2024). Unified Training of Universal Time Series Forecasting Transformers. Retrieved from arXiv:2402.02592 (cs.LG). [7] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention Is All You Need. Retrieved from arXiv:1706.03762. [8] Stankeviciute, K., Alaa, A. M., & van der Schaar, M. (2021). Conformal time-series forecasting. In Advances in Neural Information Processing Systems (Vol. 34, pp. 6216–6228).