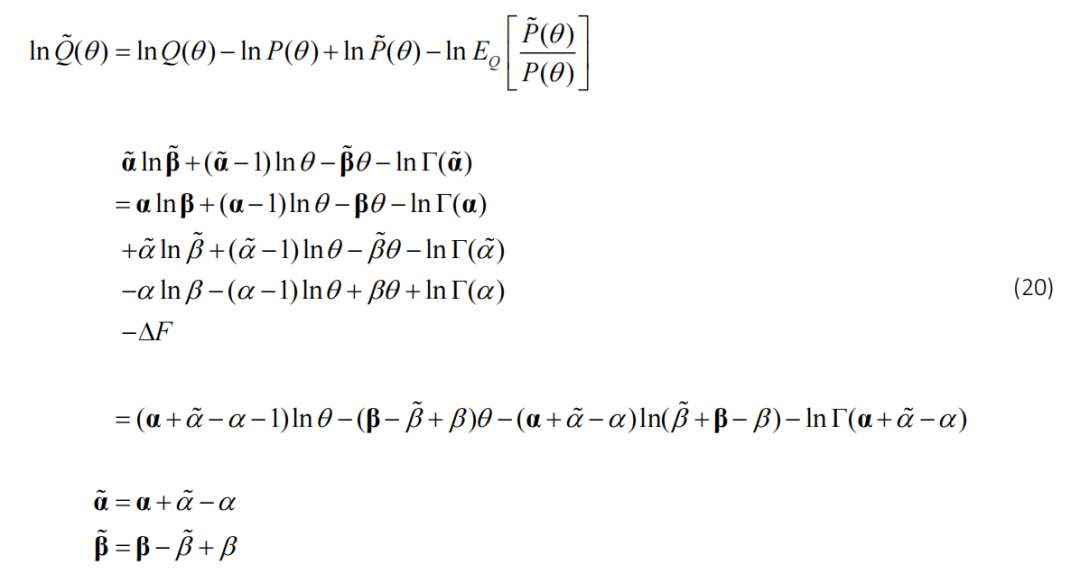每个问题的答案都是贝叶斯模型比较，假设竞争

事实上，人们常说，每个问题的答案都是贝叶斯模型比较。 这个观念有其深刻的道理。 从某种意义上说，任何问题——可以用相互竞争的假设来提出——只能通过诉诸这些假设的证据来回答。 换句话说，任何问题的答案都归结为假设或模型证据的比较，隐含在贝叶斯因子的使用中，或日志证据的差异

Summary

本文回顾了统计结构学习的最新进展；即贝叶斯模型缩减。贝叶斯模型简化是一种快速计算仅先验不同的概率模型的证据和参数的⽅法。在变分贝叶斯的设置中，这有一个解析解，它巧妙地解决了模型比较或结构学习中大模型空间的评分问题。在本技术说明中，我们回顾了贝叶斯模型简化并提供了几个离散和连续概率分布的相关⽅程。我们提供了多元线性回归、高斯混合模型和动态系统（动态因果建模）背景下的工作示例。这些示例附有重现结果所需的 Matlab 脚本。最后，我们简要回顾了神经影像和神经科学领域的最新应用。具体来说，我们考虑结构学习和分层或经验贝叶斯，它们可以被视为神经生物学过程（如溯因推理）的隐喻。

关键词：贝叶斯⽅法，经验贝叶斯，模型比较，神经生物学，结构学习

1. Introduction

在过去的几年里，贝叶斯模型比较和结构学习已成为神经科学中的关键问题（Collins and Frank, 2013; Friston et al., 2017a; Salakhutdinov et al., 2013; Tenenbaum et al., 2011; Tervo et al., 2017a）。，2016，Zorzi 等人，2013）；特别是在神经影像时间序列的优化模型中（Friston et al., 2015, Woolrich et al., 2009），并且作为我们的大脑必须解决的一个基本问题（Friston et al., 2017a, Schmidhuber, 1991, Schmidhuber, 2010） ）。事实上，人们常说，每个问题的答案都是贝叶斯模型比较。这个观念有其深刻的道理。从某种意义上说，任何问题——可以用相互竞争的假设来提出——只能通过诉诸这些假设的证据来回答。换句话说，任何问题的答案都归结为假设或模型证据的比较，隐含在贝叶斯因子的使用中，或日志证据的差异（Kass 和 Raftery，1995）。本技术说明回顾了一种称为贝叶斯模型简化的相对较新的程序，该程序目前在神经科学中常规用于数据分析（Friston 和 Penny，2011；Friston 等人，2015；Friston 等人，2016）和理论神经生物学（Friston 等人） 等，2017a）。贝叶斯模型简化背后的基本思想很简单，并且可以在各个领域找到有用的应用。

考虑某些数据y的统计模型，其参数为θ。数据的生成或前向模型包括两个部分 - 在特定参数设置下观察到一些数据的可能性

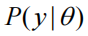
和先验概率密度P(θ)。这两者之间的平衡决定了参数自由解释数据的程度。例如，具有高方差（低精度）的高斯先验参数将很容易受到数据的影响，而具有低先验方差（高精度）的参数将受到限制，接近其先验期望值。这种使用先验的方式，有效地“关闭”参数 - 通过将其固定在某些预先确定的值（例如零） - 将在接下来的步骤中变得重要。在指定了先验之后，贝叶斯推断 - 也称为估计或反演 - 提供了参数的后验概率 p(θ |y )。这些后验与先验和可能性之间由贝叶斯规则相关联。

为了比较相同数据的不同模型——即执行贝叶斯模型比较——有必要评估每个模型

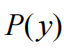
的证据。这是在特定模型下对某些数据进行采样的概率，也称为综合或边际似然。

一般来说，评估这个量是一个棘手的分析问题（由于方程 1 第二行的积分），通常使用近似贝叶斯推理来解决。这些方法在典型的计算机硬件上具有不平凡的评估时间。事实上，即使是最有效的变分方法（下一节将详细介绍），对于具有小数据集的简单模型来说，也需要几秒的时间，而对于最具挑战性的问题来说，需要几小时或几天的时间。这种计算成本可能会妨碍在合理的时间内评估大型模型空间。通过引入一种有效的方案来对大量模型的证据进行分析评分，在近似贝叶斯推理的设置中解决了这个问题。

我们这里关心的情况如下。想象一下，我们使用贝叶斯推理方案来估计模型的参数；即，在给定先验信念和一些数据的情况下，我们优化了参数的后验概率密度。我们现在要考虑根据替代先验信念定义的替代模型。通常，这些将构成具有更精确或信息丰富的先验的简化模型，这会限制或完全消除一些自由参数（的混合）。贝叶斯模型简化提供了一种基于且仅基于原始（父或完整）先验和近似后验来评估简化模型的证据的方法。换句话说，它允许人们根据原始估计来评估一组新先验的证据。这遵循经典推理中使用的相同程序，其中 F 检验基于且仅基于一般线性模型的参数。一个明显的应用是在反转具有相对无信息（即平坦）先验的父模型后对模型空间进行评分。现在可以通过对替代模型进行评分来重新审视模型假设，其中使用精确（即减少）先验来抑制或消除各种参数组合。这使得人们能够通过探索大型模型空间来删除冗余参数并修剪模型：换句话说，它实现了一种有效的结构学习形式。

接下来，我们回顾变分贝叶斯的原理，引入约简自由能的概念，并回顾连续和离散模型的特定形式。随后的部分提供了在线性回归、高斯混合模型和通常用于建模时间序列数据的动态模型的背景下贝叶斯模型简化的工作示例。最后，回顾了神经影像学和神经生物学领域的一些实证应用（感兴趣的读者可以在原始出版物中了解）。

2. Variational Bayes

模型证据的对数 ln

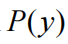
以下简称对数证据）对模型的质量进行评分，是贝叶斯模型比较的基础。然而，正如引言中所述，对数证据和随后的后验通常不能通过分析计算。在许多情况下，这可以通过转换等式中固有的困难积分问题来解决。eq1 转化为易于处理的优化问题；即，最大化对数证据的变分（自由能）界限（Beal，2003；Fox 和 Roberts，2012；Kschischang 等人，2001；MacKay，1995；Yedidia 等人，2005）。这种变分自由能在机器学习中被称为证据下界（ELBO）。相关的优化被称为近似贝叶斯推理、变分贝叶斯和变分集成学习，具有许多特殊情况，例如精确贝叶斯推理、变分拉普拉斯、贝叶斯（例如卡尔曼）过滤、期望最大化、变分消息传递、置信传播和 等等（Dauwels，2007；Kschischang 等人，2001；Loeliger，2002；Mitter 和 Newton，2003；Roweis 和 Ghahramani，1999；Yedidia 等人，2005）。简而言之，几乎每种贝叶斯模型反演和比较的（变分）方法都可以表示为优化某些数据的变分自由能函数和近似后验分布或密度（本文表示为Q）。我们关注的问题是，在先验变化的情况下，或者在添加分层约束来评估某些数据的深层或分层模型时，如何快速有效地计算这种变分自由能。

简而言之，变分贝叶斯涉及识别近似后验

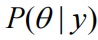
的概率密度

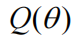
。执行优化以确定最小化近似后验和真实后验之间的差异的密度。通常使用的差异度量是 Kullback-Leibler 散度：

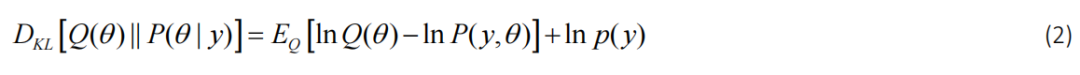
这不能直接计算，因为它取决于 p(y) 中的对数证据，其中包含方程1 中的困难积分。1. 然而，我们可以计算一个相关的函数，称为变分自由能 F（以下简称自由能），并用它来对近似的质量进行评分：

这与Kullback-Leibler散度相同，除了一个常数；即对于Q而言，对数证据是常数。“自由能”这个名称源自于统计物理学，类比地，方程式3中的两个术语被称为能量和熵。这些是在近似后验下一些数据和参数的期望对数似然，以及后验的熵。

通过将自由能表示为对一些先验信念的泛函，方程式3强调了对于任何给定的模型或先验信念，一个自由能泛函的（近似）后验是明确定义的。通过重新排列，一些有用的自由能性质变得明显：

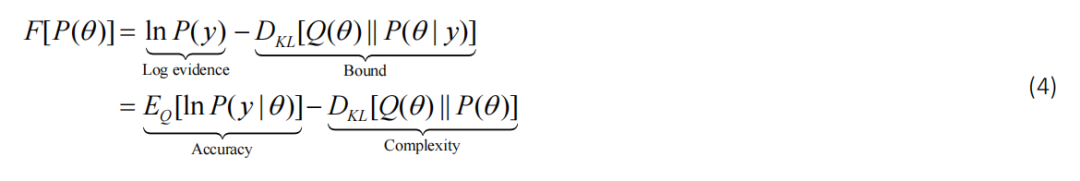
第一行显示自由能是对数证据减去近似后验和真实后验之间的 Kullback-Leibler 散度（即非负界）。这意味着最大化自由能使得近似后验尽可能接近真实后验。如果近似后验的假设形式与真实后验一致，那么我们就有了精确的贝叶斯推理，并且自由能成为对数证据。第二行表明自由能也可以表示为准确度减去复杂度，其中复杂度是近似后验信念和先验信念之间的差异。

通常，近似后验被分解为未知参数子集的边际：

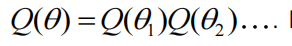
例如，控制某些数据的均值和方差的参数可以假设为彼此独立。这被称为平均场近似，可以大大简化模型反演；即关于边际后验的自由能最大化。使用变分微积分，可以直接证明任何参数子集的近似后验是其马尔可夫毯子下的预期对数概率：

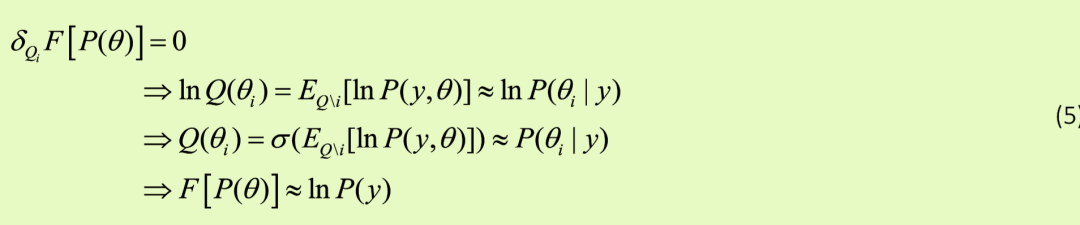
其中，

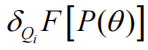
是自由能在第i个参数子集下的泛函导数，σ表示softmax函数或归一化指数，而

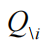
表示第i个子集的马尔可夫毯（Beal，2003）。这表明当自由能最大化时，对于每个分区i的最佳后验近似是数据和参数的对数联合概率的期望。这个期望是在所有其他分区的参数

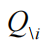
的情况下进行的，这些参数被固定。因此，通过使用任何适当的优化方案来最大化自由能；例如（Friston等人，2007年，Ranganath等人，2014年），

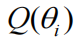
和F近似等于后验和对数证据。请注意，对于接下来的内容，唯一的先决条件是已经估计了模型的后验和自由能 - 不应用均场近似的优化方案同样合适（参见Ranganath等人，2016年，Rezende和Mohamed，2015年，Salimans等人，2015年）。

3. Bayesian model reduction and reduced free energy

我们现在转向贝叶斯模型简化所解决的问题：根据完整模型的先验和后验评估简化模型的自由能和参数。考虑为简化模型表达的贝叶斯规则，其中原始先验

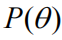
已替换为简化先验

：

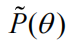
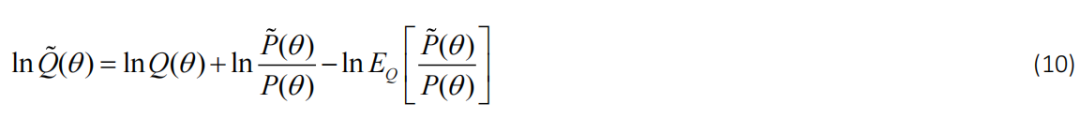
这是通过用完整模型和简化模型（方程 4 和方程 9）的自由能代替方程 4中各自的对数证据来获得的。 这些（近似）等式意味着，在给定完整模型的后验概率的情况下，人们可以评估任何简化模型的后验概率和证据。换句话说，

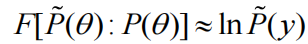
允许我们跳过简化后验

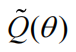
的优化，并使用完整模型的优化后验来计算证据（并且直接简化模型的后验）。一些读者会认为这是 Savage-Dickey 密度比（Savage，1972，Verdinelli 和Wasserman，1995）对任何新先验的概括。至关重要的是，在近似贝叶斯推理的变分设置中，可以直接对简化后验进行分析评估，因为它具有已知的形式 - 正如我们将在下面的示例中看到的。

可以使用下一节详细介绍的近似后验的特定（指数）形式的解析表达式来快速评估方程 9 和 10。顾名思义，贝叶斯模型简化只能用于当所有感兴趣的模型都可以转换为父模型或完整模型的简化形式时进行贝叶斯模型比较；换句话说，完整模型必须包含将要考虑的任何模型的所有参数。这意味着人们无法比较具有完全不同形式的模型。然而，在实践中，大多数模型比较往往是根据具有和不具有关键（组）参数的模型来构建的。接下来，我们将研究连续和离散数据模型的近似后验普遍形式的贝叶斯模型简化。

4. Variational Laplace

当假设近似后验

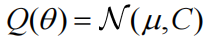
为高斯分布时，变分拉普拉斯对应于近似贝叶斯推理。在拉普拉斯假设下，近似后验能和自由能的简化形式具有简单的形式：详细信息请参见 Friston 和 Penny (2011)。

这里，

分别是先验精度和协方差，而

分别是对应的后验精度和协方差。先验期望值分别为

在完整模型和简化模型中),而后验期望值为

。在方程11中的最后一个等式定义了自由能的变化 ΔF,对应于变分对数贝叶斯因子。这是通过将概率密度函数的高斯形式代入方程9中推导出来的;请参阅Friston和Penny（2011）。请注意，当通过将其先验方差收缩到零来从模型中删除参数时，先验和后验矩变得相同 并且该参数不再对简化自由能产生贡献。实际上，方程11允许我们以简化自由能的形式评分任何简化模型或先验，同时直接评估其参数的后验分布。当后验和先验具有以浓度先验参数化的Dirichlet分布时，离散状态空间模型的相应形式如下。

5. Bayesian model reduction for discrete models

在离散模型的背景下，后验具有分类分布（并且根据浓度参数指定共轭狄利克雷先验），贝叶斯模型简化变得非常简单：通过将贝叶斯规则应用于完整模型和简化模型，可以直接显示自由能的变化（即对数贝叶斯因子）可以用后验浓度参数 a、先验浓度参数 a、定义简化或更简单模型的先验浓度参数 ã以及随后的简化后验 a 来表示。使用 B(•) 表示多元 beta 函数，我们得到（Friston et al., 2017a）：

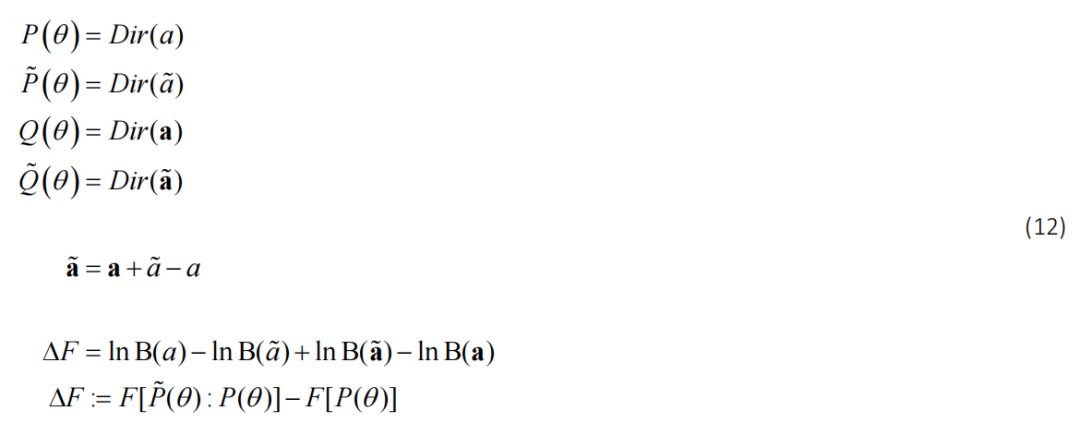
如果我们开始用更简单的先验信念观察结果，这个方程返回了我们将观察到的自由能差异。这提供了接受或拒绝由浓度参数编码的替代假设（或简化模型结构）的标准。例如，如果生成模型包含从离散（未知）原因到（已知）结果的似然矩阵映射，则可以使用分类分布和狄利克雷先验来参数化似然映射。从原因到结果的后验映射然后获得狄利克雷形式，该形式可以在证据积累过程中减少。换句话说，通过评估相应先验浓度参数设置为零时自由能的变化，可以比较具有或不具有特定原因和特定结果之间映射的模型。这使得能够非常有效地修剪离散状态和结果模型中的冗余参数；例如马尔可夫决策过程和隐马尔可夫模型。直观上来说，这种形式的结构学习可以通过删除参数来简化模型，从而比隐式精度损失更大程度地降低复杂性（参见公式 4）。我们将在下面看到一个例子，用于模拟大脑如何实现这种隐式结构学习形式。

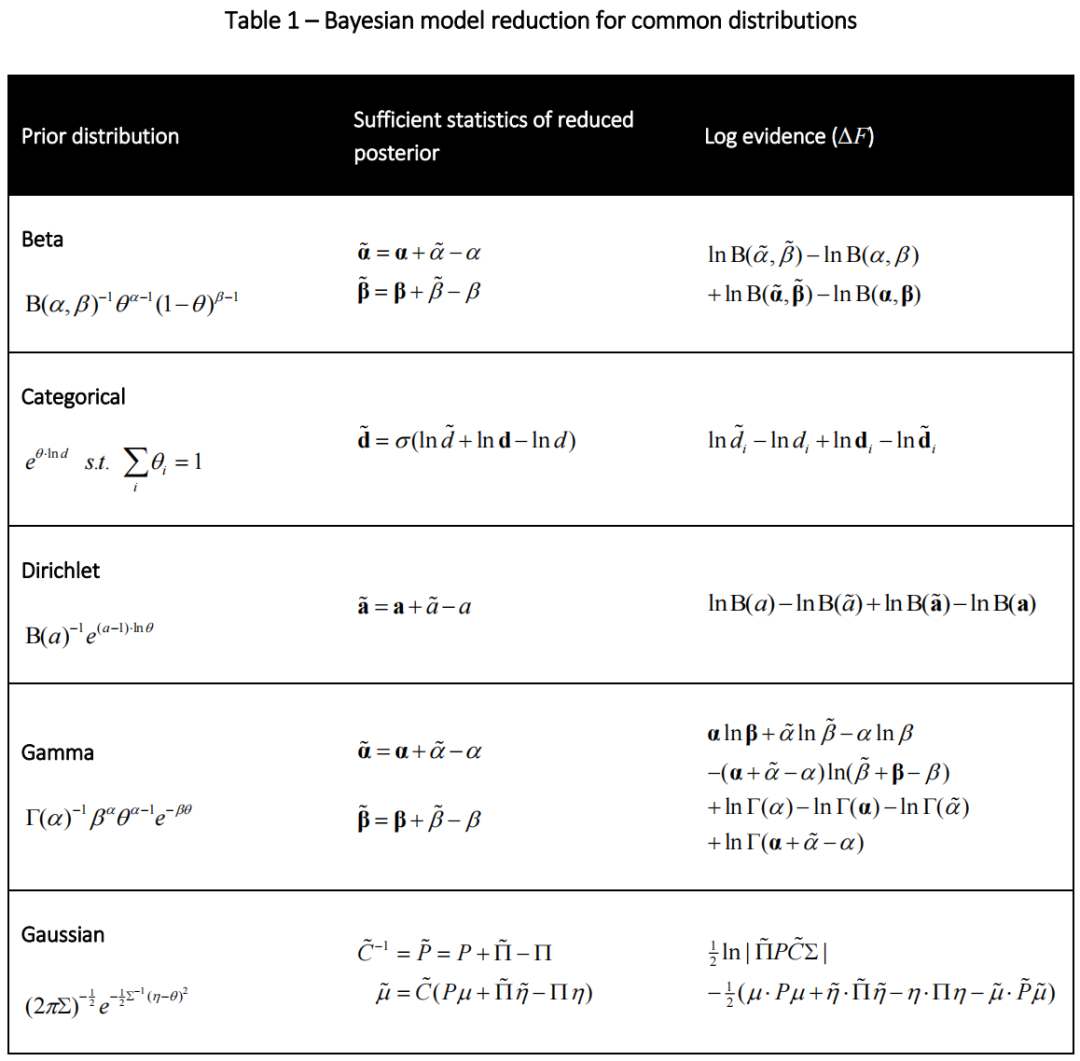
除了高斯分布和狄利克雷分布之外，贝叶斯模型简化还可以应用于一系列指数族分布。表 1 概述了简化后验的形式以及一些常见分布的证据。请注意 beta 和 Dirichlet 表达式以及多项分布和分类分布形式的相似性。这种形式上的相似性是因为这些分布是彼此的特例。这些分布的其他特殊情况，例如二项式分布（多项式的特殊情况），具有相同的形式。使用 softmax 函数 (σ) 来表示分类和多项式简化后验，该函数对其参数求幂，然后对其参数进行归一化。作为说明性示例，附录中提供了 Gamma 分布的简化证据和后验的逐步推导。

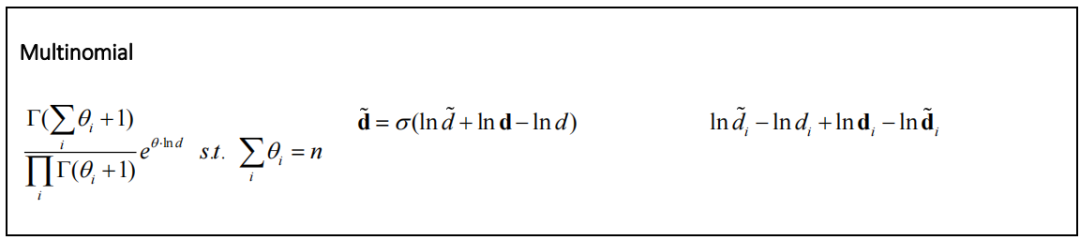
6. Worked examples

在本节中，我们提供静态和动态、线性和非线性模型背景下贝叶斯模型简化的工作示例。用于生成图形的关键 Matlab 例程在括号中给出（例如，spm_dcm_bmr.m）。有关这些示例的模型规格的完整详细信息，以及要使用 Matlab 运行示例，我们建议读者参阅随附的代码文档（请参阅软件说明）。

6.1 Linear regression

第一个示例演示了在一般线性模型的背景下找到解释一组观察到的数据所需的最佳回归量（协变量或解释变量）集：

然后，我们使用变分贝叶斯方案 (spm_peb.m) 以及参数和超参数的高斯先验，将一般线性模型拟合到模拟数据。这个“完整”模型有一个设计矩阵，其中包括用于生成数据的 10 个回归量，以及另外 10 个随机生成的（正交）回归量。我们测试了是否可以使用贝叶斯模型简化来恢复原始简化模型结构（即原始 10 个回归量）。我们对完整模型应用了自动迭代方案 (spm_dcm_bmr_all.m)，该方案在关闭 20 个参数的不同组合的情况下评估简化模型。这些参数已关闭 – 即固定在接近其先前期望零的值 - 通过用精确的收缩先验

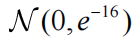
替换其原始先验密度 N(0,1) 。

每个简化模型的自由能均使用贝叶斯模型简化进行分析计算（参见表 1），并且保留自由能增加最大的模型以用于（贪心）搜索的下一次迭代。图 1A 说明了搜索最终迭代的模型空间，其中以不同方式组合 8 个参数，生成 256 个具有最大证据的简化模型。打开的参数显示为白色，关闭的参数显示为黑色。图 1B 显示了每个简化模型与完整模型相比的相对自由能。这些结果在图 1C 中可以更清楚地看到，它显示了模型的后验概率（假设模型的先验一致）。有两个模型脱颖而出 - 模型 256（84% 概率），其所有八个候选参数均已打开；模型 128（14.6% 概率），其一个附加参数（第七个参数）已关闭。

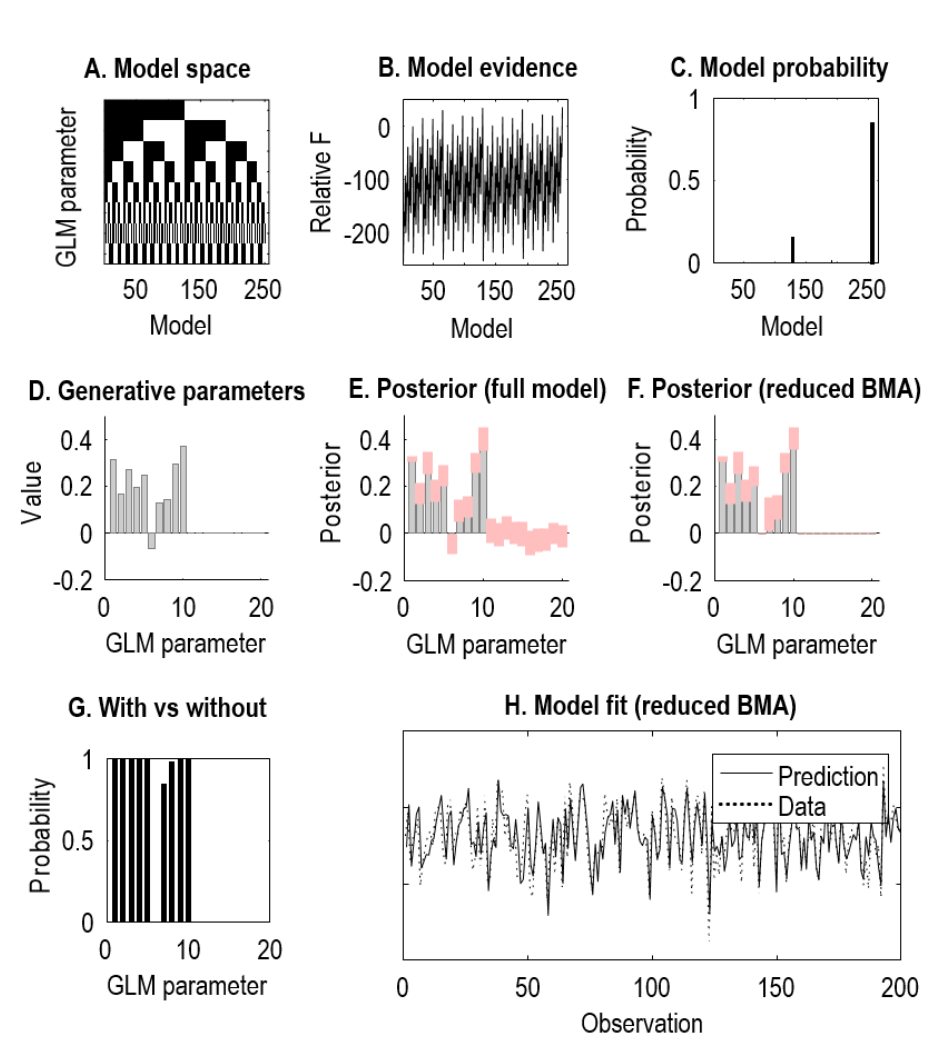
Figure 1:贝叶斯模型简化应用于一般线性模型的模拟数据。完整模型在其设计矩阵中定义了 20 个回归量，并对简化模型 A 进行了迭代搜索。来自搜索最终迭代的 256 个替代模型集。每一列都是一个模型，每一行都是一个参数。颜色表示每个参数是打开还是关闭，即白色=打开（无信息先验）和黑色=关闭（固定为先验期望为零）。B. 相对对数模型证据，通过自由能近似，相对于完整模型，使用贝叶斯模型简化进行评估。C. 模型的后验概率。最好的模型是 256 号（84% 的概率），第二好的是 128 号（14.6% 的概率）。D. 用于生成模拟数据的参数。E. 完整模型参数的后验密度。条形的高度是预期值，粉色误差条是 90% 的可信区间。还估计了参数之间的协方差，但此处未显示。F. 所有候选模型参数的贝叶斯模型平均值 (BMA)。参数 11-20 已正确关闭，参数 6 也是如此。G. 每个参数存在的后验概率。每个条形图显示了打开某个参数的所有模型与关闭该参数的所有模型的比较结果。H. 在面板 F 所示的参数下模型（实线）和残差（虚线）的预测。

图 1 的第二行将用于生成模拟数据的参数（图 1D）与完整模型恢复的参数（图 1E）以及最终 256 个简化模型的平均参数（图 1F）进行了比较。这是使用贝叶斯模型平均 (BMA) 计算的，这意味着每个模型对平均值的贡献通过模型的后验概率进行加权（Trujillo-Barreto 等，2004）。这种平均形式正确地承认了模型的精确形式或结构的不确定性。从图 1F 可以看出，冗余回归参数（编号 11-20）已从模型中正确修剪。在生成数据的参数（编号 1-10）中，有一个参数设置为零（编号 6），表明考虑到模拟数据中的观测噪声水平，其效应量太小而无法检测到。换句话说，包含此参数并不能充分提高模型的准确性以证明额外的复杂性是合理的。

图 1G 显示了每个参数存在与不存在的概率，该概率是通过对每个参数执行单独的系列模型比较来计算的（Penny 等人，2010）。换句话说，对于每个参数，将打开该参数的所有模型的汇总证据与关闭该参数的所有模型的汇总证据进行比较。这个结果表明，我们可以确信所有保留参数的存在概率接近统一，除了参数 7 之外，它的概率只有 85.2%。最后，图 1H 显示了在贝叶斯模型平均值的参数下，实际数据（虚线）与模型预测的数据的对比。

总之，此示例说明了贝叶斯模型简化背景下使用的关键过程。使用变分贝叶斯方案将具有 20 个参数的“完整”一般线性模型拟合到数据，提供参数的后验概率和对数证据的自由能近似。然后，使用贝叶斯模型简化和自动迭代搜索对数千个简化模型进行评分（几秒钟内）。使用贝叶斯模型平均来总结最佳简化模型的参数后验，并使用家庭贝叶斯模型比较来计算每个参数的概率。至关重要的是，由于使用贝叶斯模型简化，只需将完整模型拟合到数据即可 - 所有其他模型的证据和参数均通过分析计算，使用典型的台式计算机大约需要两秒钟。

6.2 Gaussian mixture model

下一个示例说明了高斯混合模型 (GMM)，它提供了一个机会来展示应用于非高斯分布的贝叶斯模型简化的简单示例。生成模型采用图 2 所示的形式（为简单起见，假设球形单位协方差）。简而言之，对于 N 个数据点中的每一个，模型都假设一个从分类分布中提取的分类变量

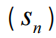
（其参数是从狄利克雷先验中采样的）。该变量指定每个簇生成数据点的概率。该变量可以采用的每个值都与高斯密度相关，具有不同的先验平均值（随机初始化）。求解该模型涉及找到每个数据点的簇责任

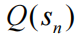
、每个簇的中心

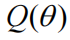
以及每个簇

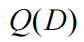
生成的数据点的比例。

解决此类推理问题的一个重要挑战是确定分类变量可以合理地取多少个值（即有多少个聚类在起作用）。为了解决这个问题，我们从比先验预期更多的聚类开始，并使用贝叶斯模型约简来消除先验聚类概率

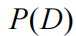
上的狄利克雷分布的聚类。此处执行模型缩减的主要好处是，在决定是否删除每个簇之前，我们不需要重新估计已删除的簇。相反，我们可以直接评估减少的模型证据，就好像我们已经删除了它一样。图 2 显示了在用一定数量的聚类拟合模型和使用贝叶斯模型简化来评估一组模型的相对证据之间交替的序列；每个都将给定簇的先验概率设置为一个小值。如果证据大于完整模型的证据，则删除相应的簇，直到恢复正确数量的簇。这提供了一个示例，说明如何在分类推理设置中使用贝叶斯模型简化来在替代数量的簇之间进行选择

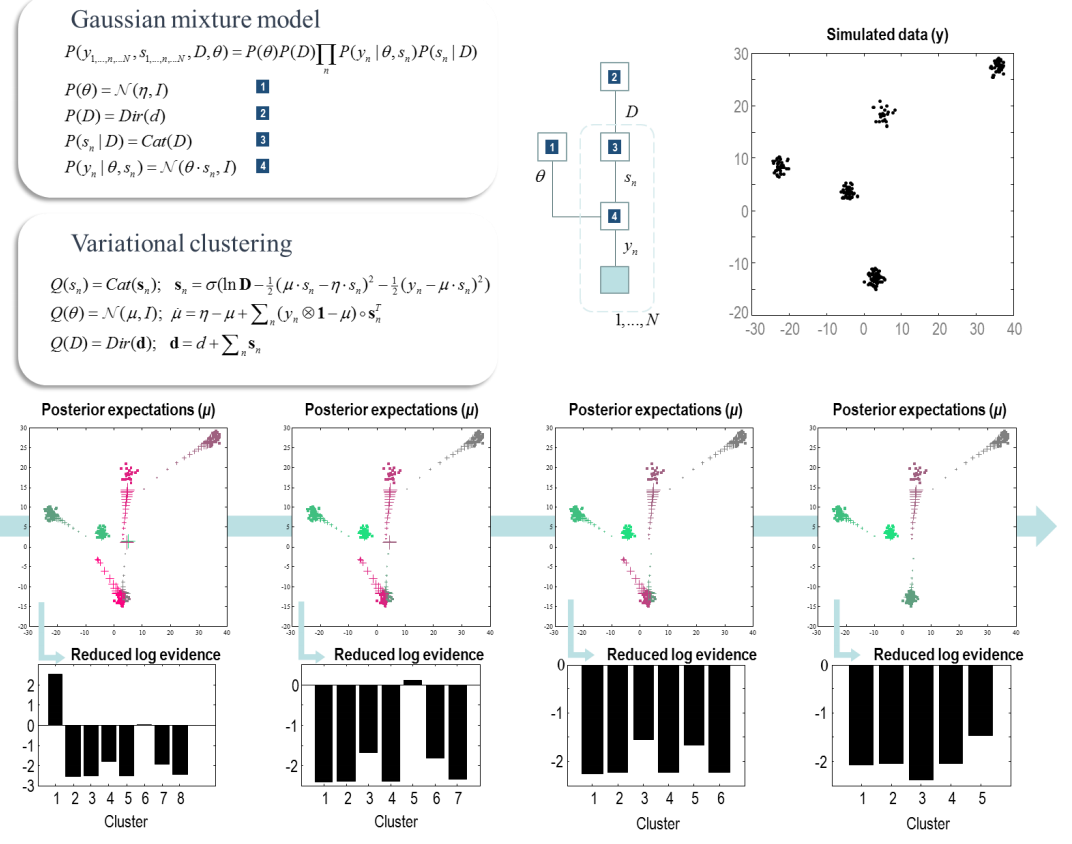
图 2：贝叶斯模型简化应用于高斯混合模型的模拟数据。左上面板显示了用于将每个数据点分配到其集群的高斯混合模型和变分聚类方案的形式。这在中心以因子图的形式显示。右上图显示了该模型生成的模拟数据，假设有五个集群。然后，我们从具有八个簇的模型开始，随机生成对其中心的先验期望，并将它们修剪掉，直到模型证据没有进一步改进，如图下半部分的图序列所示。这些图显示了

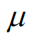
的估计值，作为十字 (+)，每个梯度步骤的大小都会增加。每个数据点的颜色表示最有可能生成它的簇。下行中显示的减少的日志证据对应于没有每个集群的模型的日志证据，相对于具有所有集群的（完整）模型。如果此日志证据大于零，则接受简化模型并删除相应的簇（即，在第一次迭代中删除第一个簇，在第二次迭代中删除第五个簇。簇的数量从六个减少） 到 5，因为我们实施了一个额外的约束，即合并似然分布相距小于 3 nat（用 KL 散度量化）的聚类对。在这个示例中，恢复了正确的聚类数量。至关重要的是，我们没有 需要拟合具有较少集群的任何模型，因为我们可以使用模型简化来说明如果我们这样做，模型证据将不会进一步增加。请参阅随附的软件代码以获取该图的动画版本。

6.3 Dynamic causal modelling

前面的两个示例说明了使用静态模型的贝叶斯模型缩减 (BMR)；然而，BMR也可以应用于基于微分方程的时间序列模型的参数。在神经影像学中，这通常是使用动态因果模型（DCM）来完成的；即时间序列数据的线性或非线性状态空间模型的变分反演（Daunizeau et al., 2011）。在这种情况下，贝叶斯模型简化可以快速对候选网络架构的证据进行评分；例如（Jafarian 等人，2019）。

在这里，我们提供一个简化的示例。考虑一个有向网络或图，由一组交互的节点（顶点）和它们之间的边组成。这些节点可以是食物网中的物种、股票市场上的公司或大脑区域。每个节点都配备有一个状态zi，用于量化，例如，一个物种的种群规模，或一家公司的价值，或一个神经元种群的突触后放电率。动态交互在该网络上进行，产生（嘈杂的）测量结果。该网络的动态可以建模如下：

方程 14 的第一行是

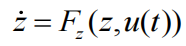
形式的任何动力学的简单模型（泰勒近似),其中 F 是某个未知函数。该模型的变体包括生态学和经济学中的广义 Lotka-Volterra 方程（参见 Hofbauer 和 Sigmund，1998）,以及神经影像学中使用的 fMRI 神经模型的 DCM（Friston 等，2003）。邻接或连通矩阵

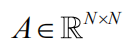
（雅可比行列式，也称为社区矩阵）编码 N 个节点之间的连接,其中

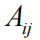
是节点 j 对节点 i 的影响力。有 R 个已知的扰动可以驱动网络中的活动,在矩阵

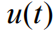
的列中编码为时间序列，其中 t 索引时间，由矩阵

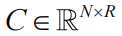
参数化。参数

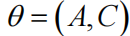
是以 Hz 为单位的速率常数。方程的第二行。图 14 描述了人们期望给定的测量结果的生成状态向量 z，通过一些线性或非线性观测函数 g 和测量误差

。

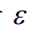
在这里，我们演示了如何使用 BMR 来识别最能解释某些数据的邻接矩阵。我们首先模拟八节点网络的时间序列（图 3）。为了生成数据，我们在矩阵 A 中配置了前馈方向 (0.5Hz) 的兴奋性连接、反馈方向 (-1Hz) 的相互抑制连接以及每个区域的自抑制以确保稳定性(-0.25Hz)。网络中的活动由二十个持续时间为一秒的“事件”驱动，这些“事件”作用于第一个节点，并具有短暂的抖动；即，C₁₁=1Hz。我们添加了以 400 精度采样的高斯观测噪声，得到 8.18Db 的信噪比（基于信号平方和与噪声平方和的比率）。为简单起见，我们将 g 设置为恒等函数 g(z) = z。

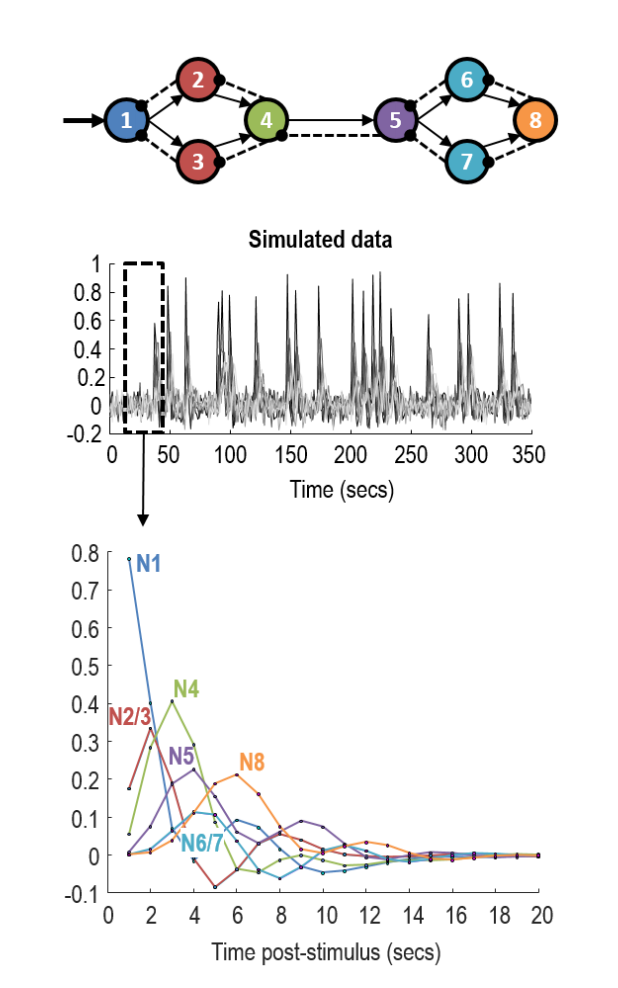
Figure 3:动态系统贝叶斯模型简化的模拟数据。模拟数据是从简单的微分方程模型生成的。顶部：模型中用于生成数据的八个节点的配置。节点之间的实线箭头表示连接矩阵 A 中的正（兴奋）值，虚线箭头表示负（抑制）值。进入节点 1 的箭头表示驱动输入，编码在矩阵 C 中（参见公式 14）。中：模型生成的模拟数据，添加了观测噪声。底部：在没有噪声的情况下，每个节点的状态 z 响应单个输入。请注意，时间优先级不是这里的关键数据特征，而是幅度的动态变化，由于每个节点上的抑制性自连接，它类似于阻尼振荡器。

接下来，我们假设我们不知道生成数据的连接结构，并且我们想使用上述方法来推断它。首先，我们对数据拟合了一个“完整”模型，并打开了 64 个区域之间所有可能的连接。这对应于弱设置邻接矩阵（连通性）参数的信息性高斯先验。变分拉普拉斯估计方案 (spm_nlsi_GN.m) 提供了该完整模型参数的后验概率密度及其证据的自由能近似。

接下来，我们进行贝叶斯模型缩减。出于说明目的，我们首先比较一小组假设驱动的简化模型，然后在大型模型空间上执行自动搜索。假设空间中有三个模型（图 4，顶部）。模型 1 是完整模型，所有节点之间的所有连接都由数据通知。模型 2 将某些连接参数（矩阵 A 的元素）固定为零，通过用精确的收缩先验

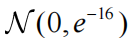
替换它们的默认先验 (0,1/16)。该模型的结构与生成数据的结构相同。Model 3 的连接数量与 Model 2 相同，但配置不同。我们使用贝叶斯模型约简来计算三个候选模型中每个模型的约简自由能。图 4（左下）绘制了这些相对于最差模型的结果。右下图是每个模型的后验概率（即自由能上的 softmax 函数）。正如预期的那样，模型 2 获胜，后验概率达到上限。因此，在仅将一个模型拟合到数据（完整模型）并分析得出两个简化模型的证据后，就推断出原始网络结构。

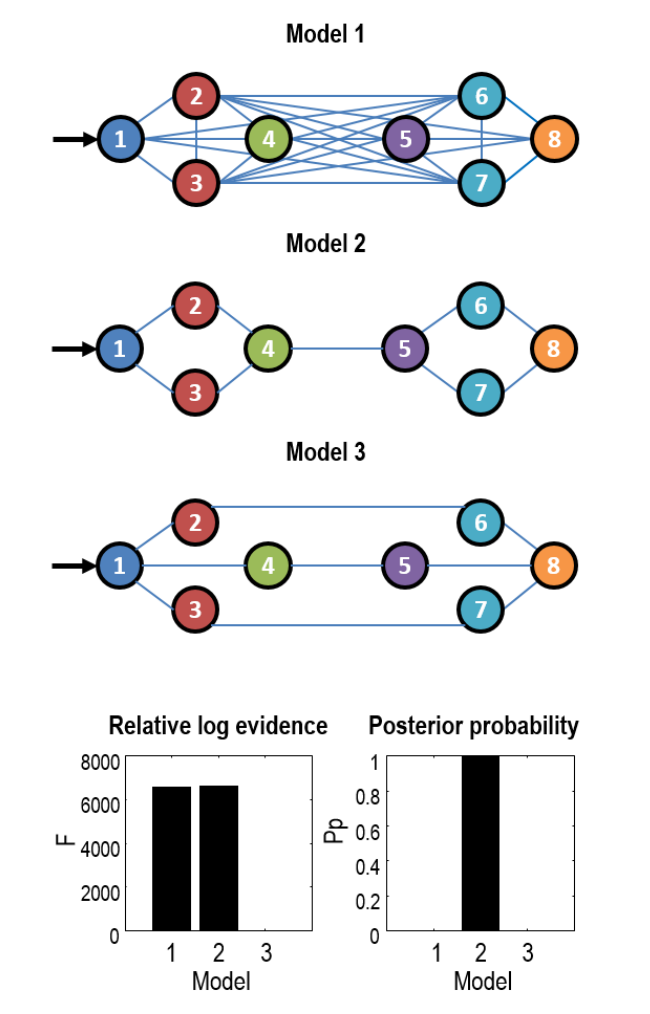
图 5 显示了贝叶斯模型简化的另一种应用，即对简化模型使用自动搜索。与上面的线性回归示例一样，这涉及从完整模型中迭代修剪参数，这样做会增加自由能。图 5 的左侧面板显示了用于生成模拟数据的模型参数，中间面板显示了使用变分拉普拉斯方案估计的完整模型参数的后验密度。顶行将这些参数显示为条形图，而底行将后验期望值排列为邻接矩阵。可以看出，完整模型包含许多未用于生成数据的连接参数，大误差线（90% 可信区间）与零重叠。图 5 的右图显示了贝叶斯模型简化的结果。原始网络架构已正确恢复，但节点 7 到节点 8 的连接除外，该连接已从模型中删除。这说明贝叶斯模型比较总是倾向于能够解释数据的最简单模型。这里，节点 8 的活动可以通过从节点 6 接收的输入来充分解释，而无需保证来自节点 7 的输入的额外复杂性成本。

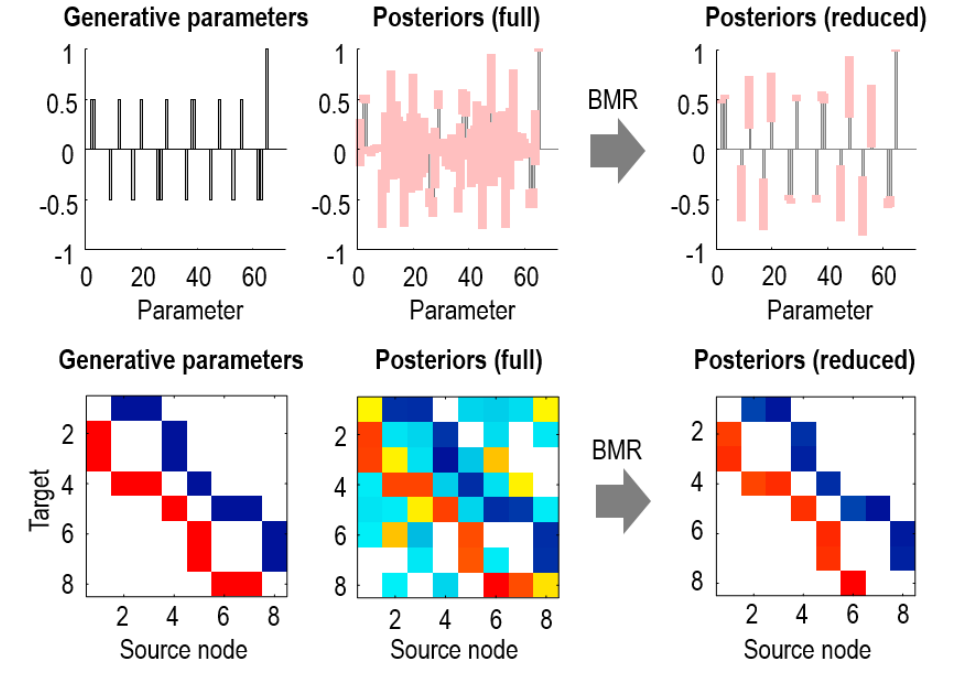
Figure 5:使用贝叶斯模型简化自动搜索简化的动态模型。顶行将模型参数显示为条形（如果可用，则具有 90% 的可信区间），底行将预期值显示为邻接矩阵。左栏：用于生成模拟数据的参数。这些被排序为从节点 1 到节点 2 的传出连接，依此类推。最终参数来自矩阵 C（驱动系统的外部输入）。中间列：完整模型的估计连接性，其中八个节点之间的所有连接均已打开。右栏：贝叶斯模型对自动（贪婪）搜索的 256 个最佳模型进行平均。恢复的参数与用于生成数据的参数非常匹配，但从区域 7 到区域 8 的连接除外，该连接不需要解释数据。

7. Empirical examples

近年来，贝叶斯模型简化在计算神经科学和生物学领域被证明是有用的。最后，我们简要回顾了应用贝叶斯模型简化的一些不同类型的模型。不可避免的是，这些例子中的大多数都来自我们自己的实验室和我们合作者的实验室，但在本文中，我们希望强调该方法的通用性。

7.1 Bayesian model comparison and structure learning

如上所述，贝叶斯模型缩减的一个有用应用是在相对信息量较小的先验条件下反转单个父模型后，对非常大的模型空间进行评分。Friston 等人利用了这一点。(2011)，其中第 6.3 节中详述的（动态因果）模型被扩展以模拟静止时大脑的动态（图 6A）。这需要使用微分方程来模拟网络动力学，并使用生物物理详细的观察模型来描述从隐藏状态（神经元反应）到功能磁共振成像（fMRI）时间序列数据的转换。当推断像这样的大型网络的连接结构时，连接的数量及其组合显然会变得非常大；从而需要一种有效的模型或结构学习方案。在此设置中，通过使用贝叶斯模型简化，可以在几秒钟内评估数千个候选模型。此示例在连续状态上使用高斯后验。有关使用贝叶斯模型简化进行动态模型结构学习的最新工作的详细调查，请参阅（Jafarian 等人，2019）。

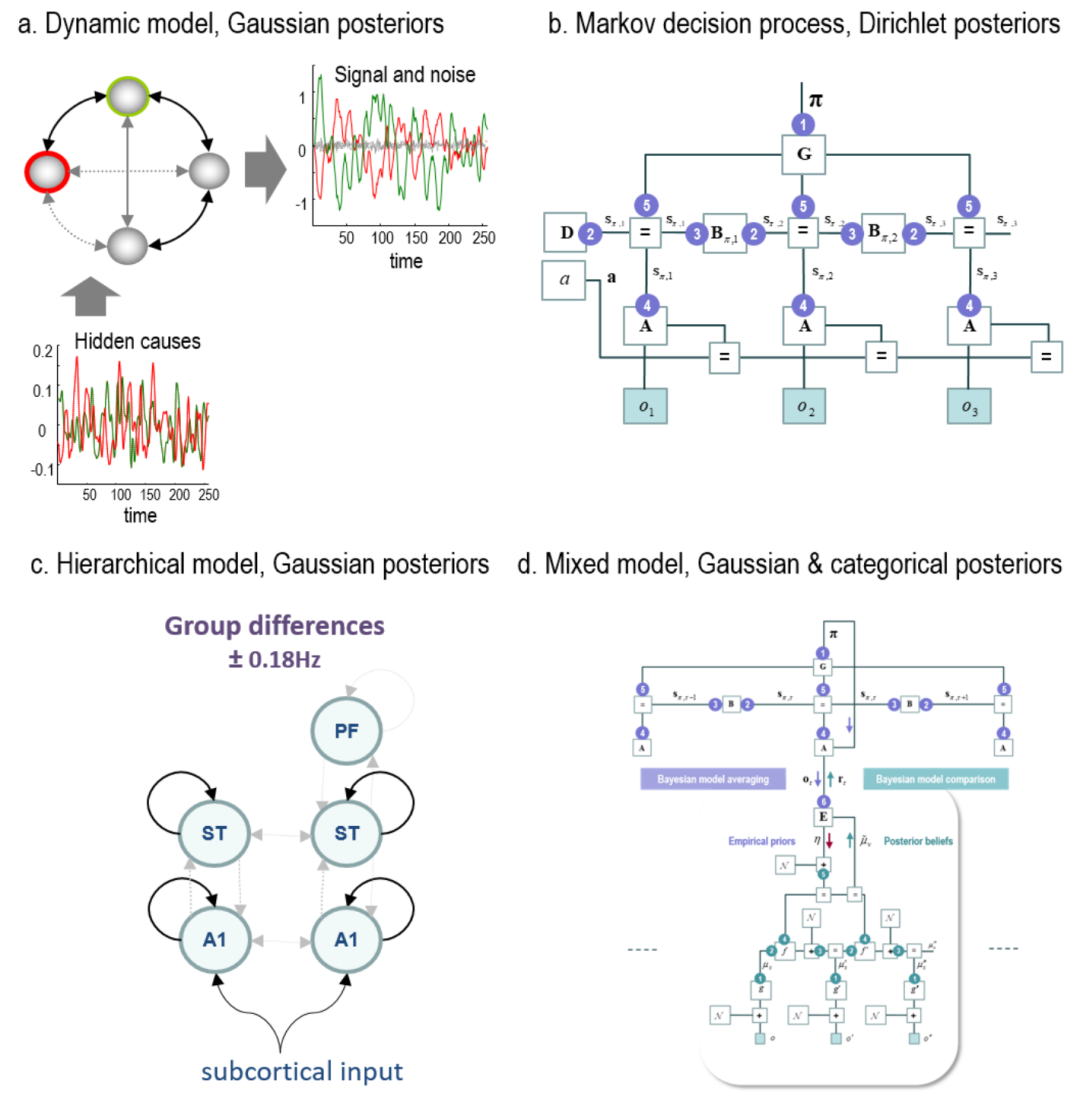
Figure 6:神经生物学和神经影像学中使用贝叶斯模型简化的示例模型。面板 A. 连续状态空间神经网络模型（左上）用于模拟功能磁共振成像 (fMRI) 数据（图 a 的右上）。随机模型反演（广义过滤）用于执行估计连接参数（细黑色和灰色箭头）和未观察到的神经活动原因（图 a 的左下角）的双重问题。然后使用贝叶斯模型简化来推断生成数据的连接架构（黑色箭头）。改编自（Friston 等人，2011）。面板 B. 用于模拟规则学习的生成模型的图形表示。该福尼因子图显示了生成模型隐含的条件依赖性。白色圆圈中的变量构成（超）先验，而蓝色圆圈包含随机变量。这种格式显示了结果 (o) 如何从隐藏状态 (s) 生成，隐藏状态 (s) 根据概率转换 (B) 演化，而概率转换 (B) 取决于策略 (π)。选择特定策略的概率取决于其预期自由能 (G)。对矩阵 A 使用贝叶斯模型简化，该矩阵对从隐藏状态到结果的似然映射进行编码。改编自（Friston 等人，2017a）。面板 C. 大脑听觉通路的连续状态空间模型，用于在组间差异的背景下模拟多个受试者的电磁反应。层次模型由第一层每个主体的连续状态空间模型和第二层的一般线性模型组成。目的是推断特定连接参数的共性和组间差异。改编自（Friston 等人，2016）。面板 D. 该图使用福尼因子图来说明集成离散（马尔可夫决策过程）和连续（状态空间）模型的消息传递方案。该图的上半部分对应于马尔可夫决策过程 - 使用相同的参数化在面板 b 中生成模型。下半部分的连续模型是状态空间模型，其参数由马尔可夫决策过程的离散结果状态决定。模型的较低层（连续）和较高层（离散）之间的通信使用贝叶斯模型简化。详情请参阅（Friston et al., 2017b, Friston et al., 2017c）。

7.2 Bayesian model reduction in biology

‍贝叶斯模型简化不仅对于数据分析和模型比较有用，而且还被用于计算神经科学和理论神经生物学的背景下。贝叶斯模型比较中固有的冗余参数的消除以及深层分层模型的优化都在这种背景下出现。消除冗余参数的生物过程的一个很好的例子是睡眠。通过大脑中突触连接的消除或退化（Tononi 和 Cirelli，2006）。

这个基本概念是使用合成（计算机）主体来建模的，这些主体对他们的世界中的突发事件进行建模（Friston 等人，2017a）。使用贝叶斯模型简化，很容易证明，简单地离线“思考事物”可以最大限度地降低模型复杂性，并带来更有效的学习。在这个例子中，模拟了一个好奇的智能体，它自发地学习了控制其行为的感官后果的规则。在虚拟实验的每次试验中，智能体都会看到三个彩色圆圈，并且可以通过引导目光来采取行动。准备好后，代理会选择颜色进行响应，并获得关于他们的响应是否正确的反馈。为了成功完成此任务，代理必须推断确定其收到的反馈的规则（例如，如果顶部的圆圈是红色，则正确的响应是左侧的颜色）。

至关重要的是，当综合受试者在每次接触感官数据（即反馈）后进行贝叶斯模型简化时，他们能够增强他们的溯因推理（即推理）。在这里，模型空间配备了额外的（超先验）约束，定义了模拟受试者所采用的模型类别（离散隐藏状态和可观察结果之间的似然映射类别）。通过最小化后续模型的复杂性（使用贝叶斯模型简化），它们被证明更适用于新数据和经验；从而提高推理和学习的效率。用于模拟规则学习的生成模型是离散时间（部分观察到的）马尔可夫决策过程（图 6b），在分类分布的参数上具有狄利克雷先验和后验。

到目前为止，我们的重点是使用减少的自由能进行模型比较、平均和选择。下一个示例说明使用相同的技术来解决分层、深度或经验贝叶斯模型中的问题（Kass 和 Steffey，1989）。

7.3 Hierarchical or deep modelling

贝叶斯模型简化已被证明在深层或分层模型的反演中是有效的。例如，假设一个人已经反转了几个对象的一些高度非线性、高维状态空间模型，现在想要在对象级别之间对模型参数进行推断；例如，（弗里斯顿等人，2015）。这必然需要某种形式的分层建模；然而，如果每次某些主题间参数发生变化时不必重新反转每个特定于主题的模型，那就太好了。在这种分层设置中，上面的约简自由能泛函找到了一个特别强大的应用，因为它总结了在分层模型的任何级别上需要知道的所有内容，就优化上面所有级别的近似后验而言。简而言之，它将完整的分层反演问题转换为一系列贝叶斯模型简化问题，其中模型连续较高级别的后验信念根据较低级别的先验和后验进行优化。

更正式地，考虑用一系列未知模型参数的条件分布表示的分层模型：

现在想象一下，我们反转了模型的第一层，同时忽略了上层的任何更高的约束。然后，我们反转模型的前两个级别，忽略第三个和更高级别，依此类推。

从上面的表达式可以看出，全层次模型的自由能可以递归地用所有下级的约简自由能来表示。换句话说，当我们添加层次约束时（模型的每个额外级别），相应的自由能可以根据新级别产生的额外复杂性以及在提供的经验先验条件下前一个级别减少的自由能来评估 按新级别：

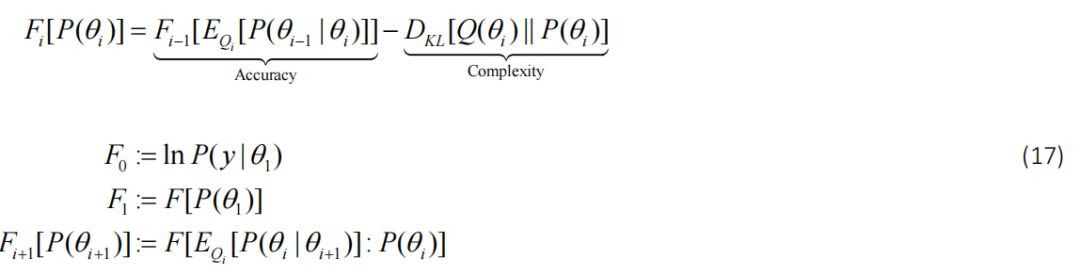
在这种情况下，减少的自由能泛函起着增强似然的作用，它具有评估模型任何级别的准确性所需的所有必要信息。这意味着我们只需要优化准确性（使用较低级别的后验和先验的自由能函数）和由于当前级别的参数而导致的复杂性。

试探性地，使用减少的自由能泛函使得人们能够以严格前馈的方式用汇总统计方法来替换对象内和对象间效应的混合效应建模中使用的分析；即，从较低级别向上传递足够的统计数据到下一个。在这里，约简自由能泛函根据较低级别参数的后验和较高级别的经验先验总结了有关较高级别参数信念的证据。

在关于后验形式的拉普拉斯（即高斯）或狄利克雷假设下，采用这种汇总统计方法时，数学上没有任何真正的改变。然而，计算时间可以大大缩短。这是因为人们不必重新访问层次模型的所有较低级别来更新较高级别提供的连续经验先验下的后验信念。（Friston 等人，2016）对此进行了说明，其中针对 16 名模拟受试者中的每一位，将具有 158 个神经元参数的神经网络模型（图 6C）拟合到模拟脑电图（EEG）数据。在一半受试者中，某些神经元参数被改变以引入组间差异（正如在患者和健康对照的比较中可能看到的那样）。然后将感兴趣的参数带到第二级（受试者间），其中通用线性模型编码共性和组间差异。使用此参数经验贝叶斯 (PEB) 方案可以正确识别表达组间差异的特定连接。至关重要的是，对受试者之间参数的后验信念的估计以及随后的贝叶斯模型简化只花了几秒钟；尽管事实上每个受试者的动态因果模型的反转可能需要一分钟左右的时间。

7.4 Deep (graphical) models in neurobiology

神经生物学的第二个例子涉及深层或分层模型的级别之间传递的（变分）消息。也许文献中最好的例子描述了一个可以执行简单形式（图像）阅读的综合主题。至关重要的是，这里的层次模型涉及时间尺度的分离以及连续（较低级别）和离散（较高级别）状态空间的混合（图 5D）。模型的较低（连续）和较高（离散）级别之间的通信使用贝叶斯模型简化，因此（马尔可夫决策过程）模型中特定隐藏状态的对数证据由自由能下界提供，使用 自由能减少。在这种情况下，模型具有高于高斯状态的高斯后验。这些用于为一组模型提供证据，每个模型都与模型更高级别的分类状态相关联。这类似于上面概述的高斯混合模型。每个分类状态的证据与其（分类）先验相结合，以标准方式计算分类后验信念。请参阅（Friston 等人，2017b，Friston 等人，2017c）了解详情。

8. Conclusion

总之，我们回顾了贝叶斯模型简化及其所依赖的自由能函数。贝叶斯模型比较的这种特殊情况依赖于任何给定模型的先验密度和后验密度的指定分析形式。在近似贝叶斯推理的设置中，这通常要求采用变分方法来进行模型拟合和随后的比较。在这种设置下 - 并且在所有有趣的模型都可以根据完整模型或父模型的先验约束来指定的约束下 - 贝叶斯模型简化已被证明非常有用。特别是，它使人们能够快速对大型模型空间的证据进行评分，例如比较具有不同稀疏结构的模型（即，通过将参数固定在先前的期望上来“关闭”不同的参数混合）。我们强调了贝叶斯模型简化的应用，该应用被证明在神经影像学中特别有用 - 深层或分层模型的反转，其中减少的自由能提供了对连续更高级别的参数信念所需证据的有效总结。另一个潜在的应用（此处未讨论）是通过将参数的后验绘制为减少先验的函数来研究参数对其先验的敏感性；从而进行敏感性或稳健性分析（Giordano et al., 2016）。强调了一些关键的应用和实用领域，希望这些基本思想可以在其他地方采用。

9. Appendix

本附录提供了伽玛分布的减少证据和后验表达式的逐步推导。Gamma 分布的先验和后验可以表示为：

将这些代入方程。9 对于减少的自由能给出：

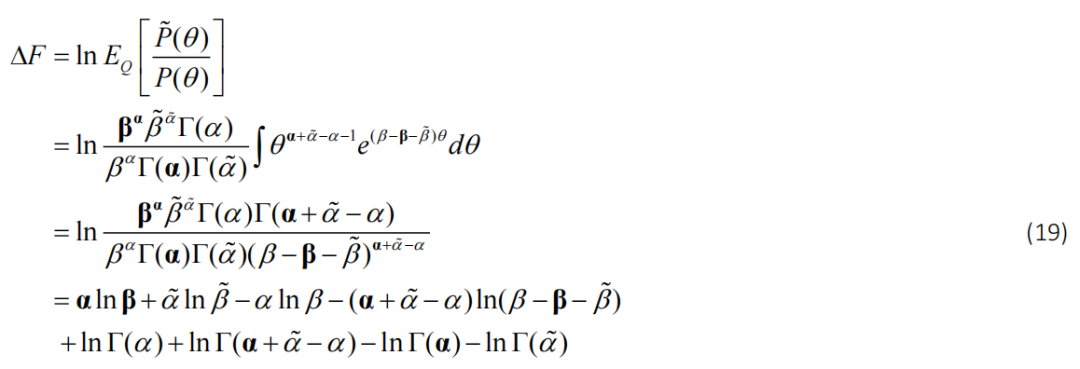
这里的第三个等式使用积分内的项与伽玛分布成比例的事实，因此积分是相关的归一化常数。对于减少后验：