机器学习入门（七）：线性回归原理，损失函数和正规方程

🍔 线性回归原理

学习目标 😀 掌握线性回归模型公式含义 😀 掌握 LinearRegression API 的使用

1. 线性回归应用场景

• 房价预测
• 销售额预测
• 贷款额度预测

话不多说，直接上图，浅显易懂！🥹

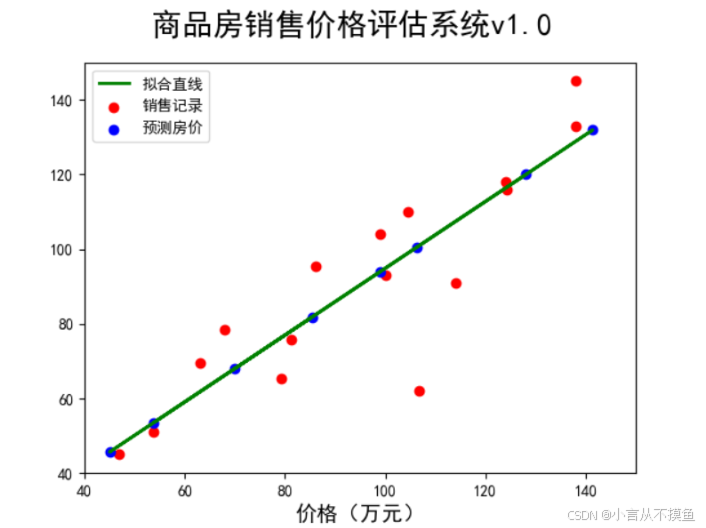
2. 什么是线性回归

2.1 定义与公式

线性回归(Linear regression)是利用 回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归。

通用公式 h(w)=w{1}x{1}+w{2}x{2}+w{3}x{3}+...+b=w^Tx+b,

其中w, x可以理解为矩阵：w= \begin{pmatrix} b \ w{1} \ w{2} \ \vdots \end{pmatrix}, x= \begin{pmatrix} 1 \ x{1} \ x{2}\\vdots \end{pmatrix}

线性回归用矩阵表示举例：

\begin{cases}1 \times x{1} + x{2} = 2 \ 0 \times x{1} + x{2} = 2 \ 2 \times x{1} + x{2} = 3 \end{cases}

写成矩阵形式🥹 ：

那么怎么理解呢？我们来看几个例子💯 ：

• 期末成绩：0.7×考试成绩+0.3×平时成绩
• 房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

上面两个例子， 我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型 。

2.2 线性回归的特征与目标的关系分析

线性回归当中主要有两种模型， 一种是线性关系，另一种是非线性关系。 在这里我们只能画一个平面更好去理解，所以都用单个特征或两个特征举例子。

线性关系 :

• 单变量线性关系🥹：

• 多变量线性关系🥹：

注释：单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系 更高维度的我们不用自己去想，记住这种关系即可

• 非线性关系🥹：

注释：为什么会这样的关系呢？原因是什么？ 如果是非线性关系，那么回归方程可以理解为： w_1x_1+w_2x_2^2+w_3x_3^2

3. 线性回归API初步使用

3.1 线性回归API

sklearn中， 线性回归的API在linear_model模块中

sklearn.linear_model.LinearRegression()

• LinearRegression.coef_：回归系数

3.2 举例

代码实现💯 ：

from sklearn.linear_model import LinearRegression
# 加载数据
x = [[80, 86],
     [82, 80],
     [85, 78],
     [90, 90],
     [86, 82],
     [82, 90],
     [78, 80],
     [92, 94]]
​
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
​
# 实例化API
estimator = LinearRegression()
# 使用fit方法进行训练
estimator.fit(x,y)
print(estimator.coef_)
# 对未知样本预测
estimator.predict([[100, 80]])

4. 小结 🍬 线性回归公式 h(w)=w{1}x{1}+w{2}x{2}+w{3}x{3}+...+b=w^Tx+b,h(w) 为目标值 🍬 线性回归公式中，w、b 代表模型参数 🍬 LinearRegression.fit 表示模型训练函数 🍬 LinearRegression.predict 表示模型预测函数

线性回归模型的目标：通过学习得到线性方程的这两个权值，如在y=kx+b中，得到k和b两个权值，并用这个方程解释变量和目标变量之间的关系。

🍔 损失函数和正规方程

学习目标 😀 掌握损失函数的概念与作用 😀 了解正规方程 😀 掌握正规方程的使用

在学习损失函数之前，我们先熟悉一下数学导数的概念🍭 ：

1. 数学导数

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。

1. 当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。
2. 导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
3. 如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率
4. 导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度
5. 不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。
   • 若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导
   • 可导的函数一定连续；不连续的函数一定不可导
   • 对于可导的函数f(x)，x↦f'(x)也是一个函数，称作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导

2. 损失函数的概念

损失函数的概念💘 ：

• 用来衡量机器学习模型性能的函数
• 损失函数可以计算预测值与真实值之间的误差（用一个实数来表示），误差越小说明模型性能越好

损失函数的作用：

• 确定损失函数之后， 我们通过求解损失函数的极小值来确定机器学习模型中的参数

先看下面的例子，有如下一组训练数据：

X = [0.0, 1.0, 2.0, 3.0]
y = [0.0, 2.5, 3.3, 6.2]

很显然，上面的数据中，X与y的关系可以近似的表示为一元线性关系， 即 y = WX

注意：当前例子中， y 和 X均为已知，由训练数据给出，W为未知

训练线性回归模型模型的过程实际上就是要找到一个 合适的W ，那么什么才是合适的W，我们先随机的给出几个W看下效果

🐻 当W = 5.0时如下图所示：

从上图中可以观察到模型预测值与真实值不同，我们希望通过一个数学表达式来表示这个差值：

• 很自然的能想到，将真实值与预测值相减并查看结果是否等于零，不为零意味着预测有误差
• 误差的大小是坐标系中两点之间的距离

我们将距离定义为： distance = \hat{y}-y

🐻 根据上面的公式， 我们可以计算出当W=5.0时预测的误差分别为：

d_0 = 0-0 = 0

d_1 = 5-2.5 = 2.5

d_2 = 10-3.3 = 6.7

d_3 = 15-6.2 = 8.8

在前面的概念中提到， 损失函数的计算结果应该为一个具体的实数，因此我们将上面所有点的预测误差相加得到：

cost(w)=d_0+d_1+d_2+d_3

cost(5) = 0+2.5+6.7+8.8 = 18

从上面的结果中发现，误差有些大，我们的模型应该还有调整的空间。

🐻 尝试将W减小，令W=0.5

根据公式 distance = \hat{y}-y， 我们可以计算出当W=0.5时预测的误差分别为：

d_0 = 0-0 = 0

d_1 = 0.5-2.5 = -2

d_2 = 1-3.3 = -2.3

d_3 = 1.5-6.2 = -4.7

cost(w)=d_0+d_1+d_2+d_3

cost(0.5) = 0-2-2.5-4.7 = -9

🐻 再尝试W=2：

根据公式 distance = \hat{y}-y， 我们可以计算出当W=2时预测的误差分别为：

d_0 = 0-0 = 0

d_1 = 2-2.5 = -0.5

d_2 = 4-3.3 = 0.7

d_3 = 6-6.2 = -0.2

cost(w)=d_0+d_1+d_2+d_3

cost(2) = 0-0.5+0.7-0.2 = 0

我们前面提到，利用损失函数可以确定损失的大小，损失越小的模型效果越好，通过对比发现

cost(5) = 0+2.5+6.7+8.8 = 18

cost(0.5) = 0-2-2.5-4.7 = -9

cost(2) = 0-0.5+0.7-0.2 = 0

当前的计算方法中

• 当W=0.5的cost的值最小，但从图像中可以看出当W=2时，模型拟合的更好
• 当W=2时计算出的误差为0，但实际情况除了d0之外其余点均存在预测误差

综上所述，我们用来衡量回归损失的时候， 不能简单的将每个点的预测误差相加

3. 平方损失

回归问题的损失函数通常用下面的函数表示💘 ：

1. yi 为第i个训练样本的真实值
2. h(xi) 为第i个训练样本特征值组合预测函数又称最小二乘法

我们的目标是: 找到该损失函数最小时对应的 w、b.

• 接下来我们开始对平方损失求解最优解

4. 正规方程

那么，该公式是得出的？

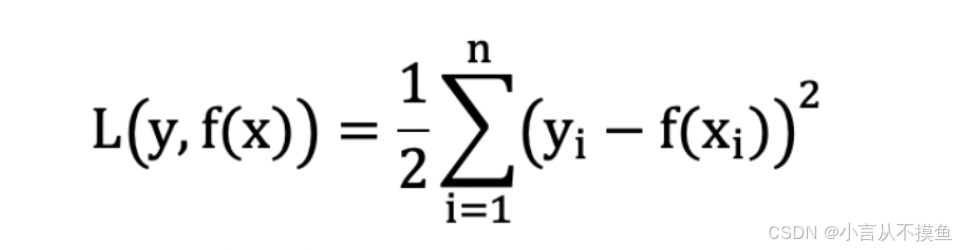
话不多说，直接上代码演示💯 :

import numpy as np
from sklearn.linear_model import LinearRegression
​
​
if __name__ == '__main__':
    
    # 特征值
    x = np.mat([[80, 86],
                [82, 80],
                [85, 78],
                [90, 90],
                [86, 82],
                [82, 90],
                [78, 80],
                [92, 94]])
​
    # 目标值
    y = np.mat([84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]).transpose()
​
    # 给特征值增加一列1
    ones_array = np.ones([len(x), 1])
    x = np.hstack([ones_array, x])
​
    # 使用正规方程公式计算 w、b
    w = (x.transpose() * x) ** -1 * x.transpose() * y
    print('[%.1f %.1f %.1f]' % (w[0][0], w[1][0], w[2][0]))
​
    # 使用 LinearRegression 求解
    estimator = LinearRegression(fit_intercept=True)
    estimator.fit(x, y)
    print(estimator.coef_[0])
​
    # 输出结果
    # [0.0 0.3 0.7]
    # [0.  0.3 0.7]

5. 小结 🍬 损失函数在训练阶段能够指导模型的优化方向，在测试阶段能够用于评估模型的优劣。 🍬 线性回归使用平方损失 🍬 正规方程是线性回归的一种优化方法