数学建模--线性规划法

简介

线性规划（Linear Programming，简称LP）是运筹学中的一个重要分支，广泛应用于资源优化、生产安排、经济分析等领域。其主要任务是在一组线性约束条件下，求解一个线性目标函数的极值问题。

基本概念

线性规划的基本形式可以表示为： 最大化𝑐𝑇𝑥最大化cTx或最小化𝑐𝑇𝑥或最小化cTx 其中，𝑐c 是一个向量，代表目标函数的系数；𝐴A 是一个矩阵，代表约束条件；𝑏b 是一个向量，代表约束条件的右端项；𝑥x 是决策变量向量，需要满足非负性条件 𝑥≥0x≥0。

线性规划的数学模型

线性规划问题通常由以下几部分组成：

1. 目标函数：一个关于决策变量的线性函数。
2. 约束条件：可以是线性等式或不等式形式的限制条件。
3. 变量的取值范围：通常要求所有变量非负。

例如，一个典型的线性规划问题可以表示为： 最大化𝑧=3𝑥1+2𝑥2最大化z=3x1​+2x2​

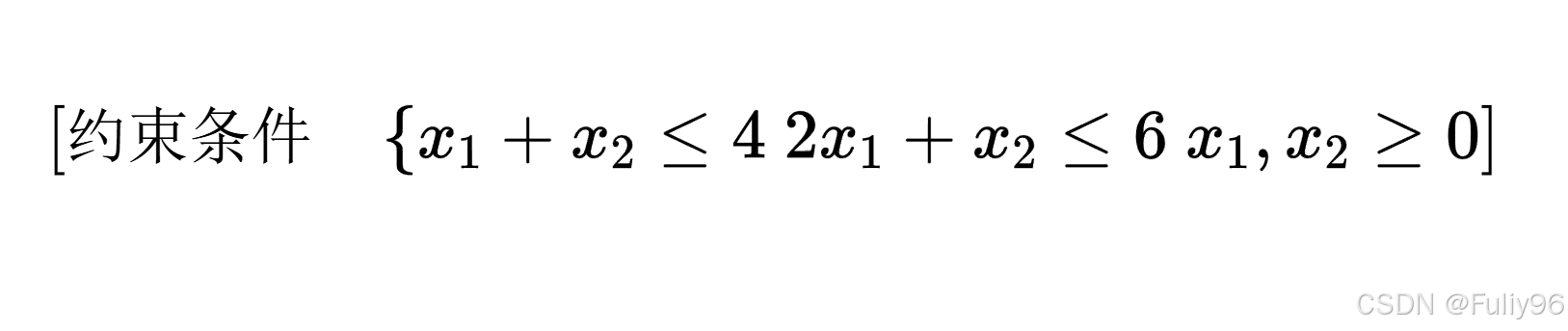
解法与算法

线性规划的求解方法多种多样，包括图解法、单纯形法、对偶理论等。其中，单纯形法是最常用且有效的算法之一。此外，还有许多其他算法如内点法、分支定界法等，用于解决更复杂的线性规划问题。

应用实例

线性规划在实际应用中非常广泛，例如：

1. 军事作战：资源分配和任务调度。
2. 经济分析：生产计划和成本控制。
3. 经营决策：库存管理和物流优化。

对偶问题

每个线性规划问题都有一个对应的对偶问题，对偶问题的最优解与原问题的最优解相同。对偶理论不仅有助于理解原问题的结构，还可以提供一些重要的经济和管理信息。

结论

线性规划作为一种重要的数学工具，在科学研究和实际应用中都具有重要地位。通过合理利用线性规划的方法和技术，可以有效地解决各种最优化问题，提高资源利用效率和经济效益。

延伸拓展

线性规划的图解法具体是如何操作的？

线性规划的图解法是一种通过图形来求解线性规划问题的方法，具体操作步骤如下：

1. 建立坐标系：在平面上建立直角坐标系，将决策变量作为坐标轴。
2. 绘制约束条件：将每个约束条件转化为等式，并在坐标系中画出相应的直线。例如，如果约束条件是 𝑥+𝑦≤6x+y≤6，则将其转化为等式 𝑥+𝑦=6x+y=6 并画出这条直线。
3. 确定可行域：通过判断各条直线所决定的半平面，找出这些半平面交出来的区域，即为可行域。
4. 绘制目标函数等值线：目标函数通常表示为 𝑧=𝑎𝑥+𝑏𝑦z=ax+by，将其转化为等值线的形式，并在图上绘制出来。例如，如果目标函数是 𝑧=2𝑥+3𝑦z=2x+3y，则可以绘制出一系列平行线。
5. 平移目标函数等值线：从一个初始点开始，沿着目标函数的法线方向（即垂直于等值线的方向）平行移动等值线，直到等值线与可行域的交点发生变化。这个过程中，目标函数的值会逐渐增大或减小，最终找到最优解。
6. 确定最优解：当目标函数等值线与可行域的交点不再变化时，该交点即为目标函数的最优解。此时，可以通过解方程组求出具体的最优解坐标。

单纯形法在解决线性规划问题中的效率和准确性如何评估？

单纯形法在解决线性规划问题中的效率和准确性可以通过以下几个方面进行评估：

1. 执行时间：虽然单纯形法在最坏情况下的执行时间并不是多项式，但在实际应用中，该算法通常相当快速。这意味着在大多数情况下，单纯形法能够迅速找到最优解。
2. 迭代次数：单纯形法通过不断设置不同的基向量，并通过矩阵的线性变换求得基可行解（即可行域顶点），并判断该解是否最优，否则继续设置另一组基向量，重复执行以上步骤，直到找到最优解。这个循环迭代的过程决定了其效率。
3. 适用范围：单纯形法是一种直接、快速的搜索最小值方法，其优点是对目标函数的解析性没有要求，适用面较广。这表明它不仅适用于简单的线性规划问题，还能处理复杂的问题。
4. 基本原理和流程：单纯形法的基本流程包括初始基可行解的寻找、判定是否为最优解以及通过旋转（PIVOT）操作不断优化解的过程。这种系统化的流程确保了其在求解过程中的准确性和可靠性。
5. 历史和稳定性：单纯形法最早由George Dantzig于1947年提出，近70年来虽有许多变形体开发，但其基本观念保持不变。这种长期的使用和验证也从侧面反映了其高效的稳定性和准确性。

对偶理论在线性规划中的应用及其对求解过程的影响是什么？

对偶理论在线性规划中的应用及其对求解过程的影响主要体现在以下几个方面： 对偶理论是线性规划中非常重要的部分，任何线性规划问题都有其对应的对偶问题。对偶问题不仅有其数学上的表达形式，还具有明显的经济含义。例如，在资源分配和成本优化中，对偶变量的最优解可以表示为资源的影子价格，即资源的替代成本。 对偶理论的一个重要应用是通过求解对偶问题来验证原问题的最优解。如果原问题和对偶问题都存在最优解，并且它们的目标函数值相等，则可以确认原问题的解是最优的。这为验证和确认最优解提供了有力工具。 对偶理论可以用于提高线性规划问题的求解效率。特别是对于大规模线性规划问题，使用对偶单纯形算法（Duality Simplex Algorithm）可以显著减少计算复杂度和时间消耗。这种方法利用了对偶问题的结构特性，使得求解过程更加高效。 灵敏度分析研究当线性规划问题的参数发生变化时，最优解和目标函数值的变化情况。对偶理论与灵敏度分析相结合，可以进行方案比较和决策分析，从而帮助决策者更好地理解和应对参数变化带来的影响。 补充松弛性条件是线性规划中的一个基本概念，它表明在最优解下，原问题的约束条件和对偶问题的变量之间存在一种互补关系。这一条件为理解和求解线性规划问题提供了重要的理论基础。 在实际应用中，对偶理论被广泛应用于生产计划、投资组合选择、运输问题等领域。例如，在资源分配问题中，通过求解对偶问题可以确定不同资源的最优分配方案，从而实现整体成本的最小化。

在实际经济管理中，线性规划的最优解是如何帮助决策者做出更明智的选择的？

在实际经济管理中，线性规划的最优解通过建立数学模型和求解最优解，帮助决策者做出更明智的选择。具体来说，线性规划能够描述经济管理工作中遇到的各种实际问题，并通过求解其最优解或最佳方案，指导企业、政府机构和银行部门等进行整体统筹规划。 例如，在生产计划中，线性规划可以帮助企业确定每天的生产时间分配，以最大化生产效率。 此外，线性规划还广泛应用于人力资源分配、广告投入、动态投资和建厂选址等热点问题的决策过程中。通过建立模型并利用相关软件进行求解，决策者可以科学地制定方针和决策，从而使用最少的人力物力资源达到最大的经济效益。这种优化方法不仅提高了企业的实际生产效率，还能在一定的人力物力资源约束条件下进行合理的资源配置。

线性规划与其他最优化问题（如二次规划、非线性规划）相比有哪些优势和局限性？

线性规划与其他最优化问题（如二次规划、非线性规划）相比，具有以下优势和局限性：

优势：

1. 求解速度快：线性规划的求解速度较快，能够快速找到最优解。
2. 模型简单：线性规划的目标函数和约束条件都是线性的，这使得模型相对简单易懂。
3. 结果准确：线性规划的结果通常比较准确，能够考虑到多个变量带来的不确定因素。

局限性：

1. 只能处理线性关系：线性规划只能处理线性关系，对于非线性问题的建模能力有限。
2. 假设限制：线性规划需要满足一些假设条件，如可加性、可分离性等，这些假设在某些实际问题中可能不成立。
3. 敏感性问题：线性规划对输入数据的敏感性较高，一些小的变动可能会导致结果的显著变化。
4. 单目标优化：线性规划只能解决单目标的优化问题，而实际问题中往往需要考虑多个目标。
5. 变量取值限制：在实际生产中，决策变量的最优值可能不是整数，而线性规划中的变量取值必须是整数。