数学建模--禁忌搜索

禁忌搜索（Tabu Search，TS）是一种元启发式优化算法，最早由美国工程院院士Fred Glover提出。它通过模拟人类智能的记忆机制来避免迂回搜索，并在局部搜索的基础上引入记忆机制以实现全局优化。

算法基本原理

禁忌搜索算法的基本流程如下：

1. 初始化：从搜索空间中随机生成一个初始解 x0x0​，并初始化禁忌表 H=∅H=∅。
2. 邻域搜索：在当前解 xixi​ 的邻域内进行搜索，构造出候选集 CN(xi,s)CN(xi​,s)，其中 ss 是当前的禁忌表。
3. 选择和更新：在候选集中选择评价值最佳的解 xnextxnext​，并更新禁忌表 HH。
4. 终止条件：如果满足终止条件（如达到最大迭代次数或解的质量不再提升），则停止计算；否则，进入下一次迭代。

关键要素

1. 禁忌表（Tabu List） ：用于记录已经访问过的解，防止算法陷入循环。禁忌表长度有限，称为Tabu-Size，可以是固定的常数或动态变化的。
2. 邻域结构：定义了当前解的邻域范围，通常通过某种方式对当前解进行小幅度修改得到新的解。
3. 评价函数：用于评估候选解的好坏，目标是找到最优解。
4. 藐视准则（Perturbation Rule） ：在某些情况下允许违反禁忌规则，以避免陷入局部最优解。

应用实例

禁忌搜索算法广泛应用于组合优化问题，如旅行商问题（TSP）、车辆路径问题（VRP）等。例如，在求解TSP问题时，可以通过构建一个包含城市间距离的图，并利用禁忌搜索算法找到最短的环路。在VRP问题中，该算法可以有效处理带有时间窗和多配送人员的复杂情况。

实现细节

1. 初始解的获取：通常采用随机生成的方式，或者使用其他启发式方法如贪婪算法生成初始解。
2. 禁忌表的管理：禁忌表需要动态更新，每次迭代后将新的禁忌对象加入表中，并移除最旧的对象以保持表的长度固定。
3. 邻域搜索策略：根据具体问题的特点设计邻域结构，确保能够覆盖足够的搜索空间。
4. 终止条件的设计：设定合理的最大迭代次数或其他终止条件，以保证算法在合理的时间内完成求解。

python代码示例

import random

# 定义距离矩阵
distance_matrix = [
    [0, 2, 9, 10],
    [1, 0, 6, 4],
    [15, 7, 0, 8],
    [6, 3, 12, 0]
]

# 计算路径总距离
def calculate_distance(path, distance_matrix):
    distance = 0
    for i in range(len(path) - 1):
        distance += distance_matrix[path[i]][path[i + 1]]
    distance += distance_matrix[path[-1]][path[0]]  # 回到起点
    return distance

# 生成初始解
def generate_initial_solution(num_cities):
    solution = list(range(num_cities))
    random.shuffle(solution)
    return solution

# 生成邻域解
def generate_neighbors(solution):
    neighbors = []
    for i in range(len(solution)):
        for j in range(i + 1, len(solution)):
            neighbor = solution[:]
            neighbor[i], neighbor[j] = neighbor[j], neighbor[i]
            neighbors.append(neighbor)
    return neighbors

# 禁忌搜索算法
def tabu_search(distance_matrix, num_iterations, tabu_list_size):
    num_cities = len(distance_matrix)
    best_solution = generate_initial_solution(num_cities)
    best_distance = calculate_distance(best_solution, distance_matrix)
    current_solution = best_solution[:]
    tabu_list = []

    for _ in range(num_iterations):
        neighbors = generate_neighbors(current_solution)
        neighbors = [n for n in neighbors if n not in tabu_list]

        if not neighbors:
            break

        current_solution = min(neighbors, key=lambda s: calculate_distance(s, distance_matrix))
        current_distance = calculate_distance(current_solution, distance_matrix)

        if current_distance < best_distance:
            best_solution = current_solution[:]
            best_distance = current_distance

        tabu_list.append(current_solution[:])
        if len(tabu_list) > tabu_list_size:
            tabu_list.pop(0)

    return best_solution, best_distance

# 参数设置
num_iterations = 100
tabu_list_size = 10

# 执行禁忌搜索
best_solution, best_distance = tabu_search(distance_matrix, num_iterations, tabu_list_size)

print(f"最佳路径: {best_solution}")
print(f"最短距离: {best_distance}")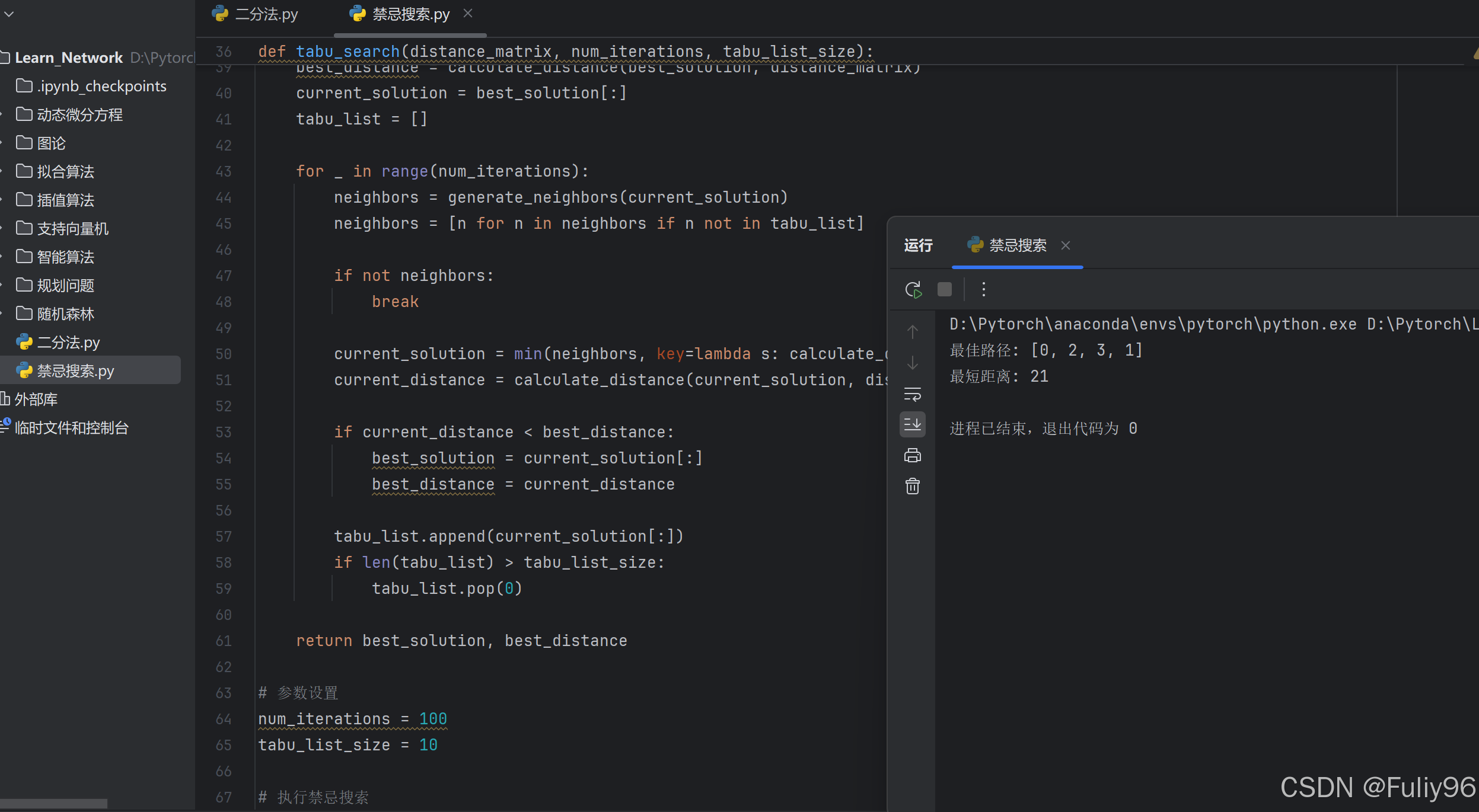

总结

禁忌搜索算法通过引入记忆机制和禁忌表来避免重复搜索，从而提高全局搜索能力。它在组合优化问题中的成功应用展示了其强大的求解能力和灵活性。通过不断改进禁忌表管理和邻域搜索策略，禁忌搜索算法在解决实际问题中表现出色。

禁忌搜索算法在解决哪些具体类型的组合优化问题中最有效？

禁忌搜索算法（Tabu Search, TS）是一种非常有效的启发式全局优化方法，广泛应用于各种组合优化问题中。以下是一些具体类型的组合优化问题，禁忌搜索算法在其中表现尤为突出：

1. 旅行商问题（Vehicle Routing Problem, VRP） ： VRP 是一个经典的组合优化问题，旨在找到一组最优的路径，使得一组车辆能够在满足一定约束条件的情况下，访问一系列客户点并返回起始点。禁忌搜索算法通过引入禁忌表和禁忌策略，避免陷入局部最优解，从而寻找更好的解决方案。
2. 多维背包问题（Multi-Dimensional Knapsack Problem, MDCVRP） ： 多维背包问题也是组合优化中的一个重要问题，禁忌搜索算法在解决该问题时也取得了显著效果。

生产调度问题涉及如何安排生产任务以最大化效率或最小化成本。禁忌搜索算法在此类问题中同样表现出色，能够有效地处理复杂的约束条件。

装箱问题通常指的是如何将物品放入最小数量的箱子中，以达到某种最优目标（如最小化总重量或体积）。禁忌搜索算法在解决这类问题时也展示了其强大的能力。

在通信领域，多用户检测是一个关键的组合优化问题，禁忌搜索算法在此类应用中也表现良好。

神经网络的训练过程是一个典型的组合优化问题，禁忌搜索算法在此类问题中也有应用。

模糊神经网络的设计同样需要解决复杂的组合优化问题，禁忌搜索算法在此类应用中也取得了成功。

生理信号的情感识别也是一个复杂的组合优化问题，禁忌搜索算法在此类应用中也展示了其有效性。

基站选址是通信网络规划中的一个重要环节，禁忌搜索算法在此类问题中能够提供有效的解决方案。

这种问题涉及到多工厂、多产品、多客户供应网络的优化策略，禁忌搜索算法在此类复杂供应链模型中表现出了优越的鲁棒性和解的质量。

总结来说，禁忌搜索算法在旅行商问题、多维背包问题、生产调度、装箱问题、通信中的多用户检测、前向神经网络训练、模糊神经网络设计、生理信号情感识别以及基站选址优化等多个具体的组合优化问题中都表现出了极高的有效性和优越性。

禁忌搜索算法的邻域结构设计有哪些最佳实践或案例研究？

禁忌搜索算法（Tabu Search, TS）是一种高效的全局优化算法，其性能在很大程度上依赖于邻域结构的设计。以下是一些最佳实践和案例研究：

1. 多邻域结构设计：
   • 在交通网络旅行商路径优化中，通过使用交换、简单逆序、插入和移位变异算子来构建初始回路的邻域，可以显著增加解空间的多样性。
   • 自适应禁忌搜索算法（Adaptive Tabu Search, ATS）采用多邻域随机变换策略，每次随机选择一种邻域对当前解进行变换，以获取候选解。这种多邻域结构有助于增强邻域解的丰富性，避免算法过早收敛，并且通过随机挑选邻域策略快速访问多个邻域。
2. 特定类型的邻域结构：
   • 2-opt和2-interchange交换邻域被广泛用于生产—库存—配送协同计划问题中，因为它们能够有效地拓展解空间并保证候选解的可行性。
   • 在基于最小负荷初始化的改进遗传算法求解柔性作业车间调度问题的研究中，介绍了OS邻域结构和MS邻域结构，这些结构通过生成邻域解并评估选择最佳邻域解作为当前解，不断迭代直至达到最大迭代次数或禁忌步长达到指定长度。
3. 结合其他优化技术：
   • 结合快速邻域切换和建立禁忌表的方法，可以增强局部寻优能力并减少重复计算时间。例如，在探针部署算法中，通过结合禁忌搜索构建禁忌表对重复的邻域动作进行限制，从而避免陷入循环搜索。
   • 混合禁忌搜索算法将最近邻算法和禁忌搜索算法相结合，用于优化配送车辆行驶路径，以降低配送成本和时间惩罚成本。
4. 理论与实际应用结合： 文献指出，选择合适的搜索空间和邻域结构是设计禁忌搜索启发式算法的关键步骤，需要充分利用对问题的理解和知识。此外，禁忌表的概念用于防止搜索陷入局部最优解之外的非改善移动，从而避免回溯到之前的步骤。

通过以上方法和案例研究，可以看出禁忌搜索算法在不同领域中的应用非常广泛且有效。

如何动态更新禁忌表以提高禁忌搜索算法的效率和性能？

为了提高禁忌搜索算法的效率和性能，动态更新禁忌表是一个关键策略。以下是几种有效的方法： 随着搜索的进行，一些先前标记为禁忌的解可能因为禁忌期限的到达而被移除禁忌表，这时新的解就可以被添加进禁忌表中以保持表的动态更新。这种方法可以避免禁忌表过载，并确保算法在不同阶段能够灵活地选择新的候选解。 禁忌表可以通过循环队列实现，这样可以保证每个被禁忌的对象都有一个固定的周期。队列长度与任务中的节点相关，通常将队列长度设置为√n，其中n表示任务图的节点数量。由于队列的先进先出特性，被禁忌对象的禁忌周期即为队列的长度。 为了避免反复遍历禁忌表，可以使用禁忌状态数组来标示所有候选邻域的禁忌状态。如果该候选解为禁忌的，则标示为1；否则为0。这样可以在每次对禁忌表进行更新时同时更新缓存数组，从而提高查询效率。 可以采用随机动态禁忌期限或系统性动态禁忌期限两种方式来确定禁忌期限。随机动态禁忌期限通常由一个定义了tmin和tmax参数的期限范围决定，其值在给定范围内随机选择，并遵循均匀分布。系统性动态禁忌期限则是在每个属性成为禁忌时为每个属性选择一个新的禁忌期限。 在某些应用中，如图像匹配问题，可以构造两种禁忌表：永久禁忌表和暂时禁忌表。永久禁忌表中的点在接下来的迭代过程中不再作为初始值，而暂时禁忌表中的点只在一定迭代次数之内禁忌被作为初始值，过了一定迭代次数后，这些点就可以成为迭代初始值，用来构建候选解邻域。

禁忌搜索算法与其他元启发式优化算法（如遗传算法、粒子群优化）相比，有哪些优势和劣势？

禁忌搜索算法（Tabu Search, TS）与其他元启发式优化算法如遗传算法（Genetic Algorithm, GA）和粒子群优化（Particle Swarm Optimization, PSO）相比，具有以下优势和劣势：

优势：

1. 快速收敛：禁忌搜索算法在求解过程中具有较快的收敛速度。这是因为该算法通过记忆机制避免了重复探索已访问过的解空间，从而加快了全局搜索的速度。
2. 强大的局部搜索能力：禁忌搜索算法特别擅长于从一个较好的初始结构开始，迅速找到并优化该结构，这使得它在某些问题上能够更快地达到全局最优解。
3. 鲁棒性：在处理复杂的优化问题时，禁忌搜索算法表现出较强的鲁棒性。例如，在多工厂、多产品、多客户供应网络的优化策略中，禁忌搜索算法比混合遗传算法更有效。
4. 解的质量：在特定问题如软硬件划分问题中，禁忌搜索算法能够提供比其他启发式算法更好的解质量。

劣势：

1. 搜索空间限制：禁忌搜索算法的搜索空间是有限的，因为其依赖于记忆机制来避免重复探索。这意味着在某些情况下，它可能无法覆盖整个解空间，从而影响最终解的质量。
2. 参数设置复杂：禁忌搜索算法需要合理设置多个参数，如邻域结构、禁忌列表长度等，这些参数的选择对算法性能有显著影响。不当的参数设置可能导致算法效率低下或效果不佳。
3. 计算资源消耗：尽管禁忌搜索算法在某些情况下表现优异，但其计算资源消耗通常较大，特别是在大规模问题中，这可能限制其应用范围。

总结来说，禁忌搜索算法在快速收敛和局部搜索能力方面具有明显优势，尤其适用于那些需要快速找到高质量解的问题。

在实际应用中，禁忌搜索算法处理大规模问题的性能表现如何？

在实际应用中，禁忌搜索算法处理大规模问题的性能表现总体上是积极的。根据多项研究和实验结果，禁忌搜索算法在解决大规模优化问题时具有显著的优势。 禁忌搜索算法被认为比较适合解决大规模问题。其基本思想是在极值附近设置禁忌标识，以避免陷入局部最优解，并通过多样的遍历策略保证种群多样性，从而提高全局搜索能力。这种全局邻域搜索方法使得禁忌搜索能够有效地探索解空间，找到较好的近似解。 具体来说，在一些实际应用中，禁忌搜索算法的表现尤为突出。例如，在多选择软硬件划分问题的研究中，禁忌搜索算法求得的近似解比模拟退火算法更接近精确解，且在大规模问题上的表现优于其他启发式算法。此外，针对带时间窗车辆路径问题的研究也表明，禁忌搜索算法能够在较大规模的问题上找到可行解，而其他方法如CPLEX可能无法求解成功。 然而，尽管禁忌搜索算法在处理大规模问题时表现出色，但其性能还受到多种因素的影响。例如，领域结构和操作方式对算法的优化时间性能有重要影响。若领域结构决定了大量的领域解（尤其对大规模问题），则可以仅尝试部分互换的结果，以改善算法效率。另外，禁忌列表长度、邻域构造算子的选择以及随机搜索策略等参数设置也会直接影响算法的运行时间和最终解的质量。 总结而言，禁忌搜索算法在处理大规模问题时表现良好，特别是在需要全局搜索和多样化解空间的情况下。