论文精读 | 2023 [PR] DDGCRN：用于交通流量预测的分解动态图卷积循环网络

时空探索之旅

发布于 2024-11-19 16:15:37

6190

文章被收录于专栏：时空探索之旅时空探索之旅

题目：A Decomposition Dynamic graph convolutional recurrent network for traffic forecasting

作者：Wenchao Weng（翁文超）, Jin Fan（樊谨）, Huifeng Wu, Yujie Hu, Hao Tian, Fu Zhu, Jia Wu

机构：杭州电子科技大学，麦考瑞大学

网址：https://www.sciencedirect.com/science/article/abs/pii/S0031320323003710

代码：https://github.com/wengwenchao123/DDGCRN

1 存在问题

（1）在早期的研究中，研究人员使用一些先验知识（如路段距离、POI相似度）来构建一个表示空间相关性的图结构。然而，由先验知识构造的邻接矩阵与任务没有直接关系，而是完全依赖于先验知识和构造方法的合理性，导致邻接矩阵的表达能力有限，同时会限制任务场景的泛化性。所以如何脱离这些限制来构建动态图以提升模型的泛化性是一个重要的挑战。

（2）交通信号自然包含两种信号，即代表正常交通流量的正常信号和代表由于未知原因导致的异常流量的异常信号。目前的交通预测方法通常将所有交通信号视视为一个整体进行预测。然而，异常信号与正常信号存在明显差异并不一样。例如，高速公路上的日常交通流量通常会向一个明确的目的地移动。因此，交通通常沿着预定的轨迹流动。然而，在异常情况下，如交通事故，一些车辆可能会改变其目的地。如何有效区分两种信号并分开建模，是一个值得研究的问题。

2 贡献

一种动态图的生成方法。该方法首先基于交通信号中的时间信息生成时空嵌入。然后将这些时空嵌入与从交通信号中提取的动态信号相结合，生成动态图嵌入，用于生成动态图。这样，该方法就可以在没有任何先验知识的情况下生成动态图结构来提取空间特征。

提出一种高效、有效的交通预测框架DDGCRN。我们的框架分别区分了正常和异常的交通信号和模型。通过分析时空embedding的情况，我们可以研究交通状况与时间点之间的关系。

是一种新的训练策略，克服了DDGCRN在效率和资源利用方面的不足。这种训练策略减少了训练早期阶段的时间和记忆消耗，且不影响模型的最终效果。

在6个交通数据集的综合分析证实了DDGCRN的有效性。与目前最先进的模型相比，DDGCRN产生的预测误差明显更低。

3 符号说明

交通路网 我们将路网表示成图

\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})

,其中

\mathcal{V}

是一组数量为

的节点，其表示路网对应位置的传感器，负责记录传感器所在位置的交通信息；

\mathcal{E}

是一组边；

\mathcal{A}

是一个邻接矩阵，其可以根据节点之间的成对道路网络距离或数据驱动等方式得到。本文采用了动态邻接矩阵，其可以表示为

A^{d}\in R^{N \times N}

。

交通信号 交通信号

X_{t}\in R^{N \times C}

表示在时间步

时交通网络

上所有传感器的观测值，其中

为传感器收集到的特征数。

交通预测 给定过去

个时间步的历史交通信号

\chi_{P}=[x_{t-P+1},...,x_{t-1},x_{t}]\in R^{P \times N \times C}

，交通预测的目的是预测

个未来时间步的未来交通信号

\gamma_{Q}=[y_{t+1},y_{t-1},...,y_{t+Q}]\in R^{Q \times N \times C}

。

GCN 图卷积运算可以用一阶切比雪夫多项式展开来很好地逼近，并推广到高维GCN，其可以表示为：

Z=(I_{N}+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})X\Theta+b

其中

A\in R^{N \times N}

是图的邻接矩阵，其是一个半正定矩阵，

是

的度矩阵，

X \in R^{N \times C}

和

Z\in R^{N \times F}

是GCN层的输入和输出，

\Theta \in R^{C \times F}

和

b \in R^{F}

代表可学习的权重和偏差。

时间和空间特征 假设交通路网中有N个节点，传感器采样数据频率为每天次，同时一周有7天，则空间和时间特征能够保存在三个独立的embedding矩阵中，

E\in R^{N \times D}

T^{D}\in R^{N_{d} \times D}

T^{W}\in R^{N_{w} \times D}

，它们都是可训练的参数，

为embedding dimension。

4 模型框架

DDGCRN主要由四个部分组成，分别是STE generator，DGCRU以及Forecast和Backcast层。

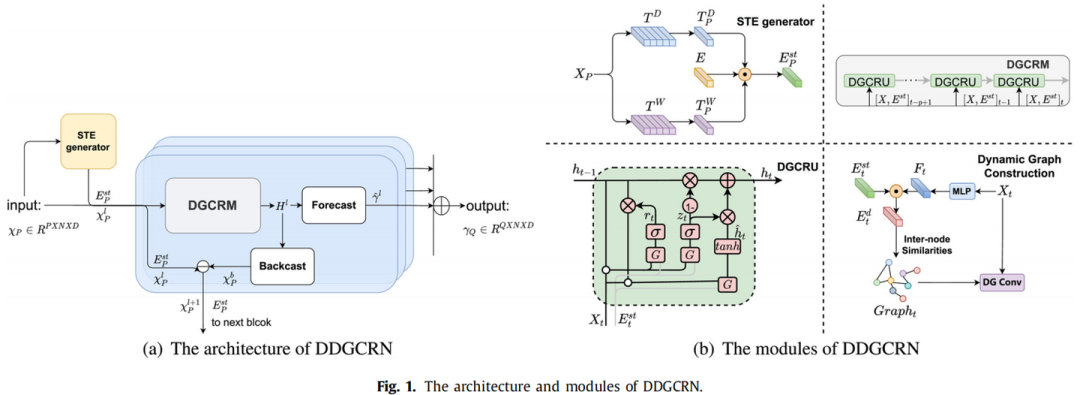
DDGCRN

4.1 Dynamic graph generation

DDGCRN包括一种动态图生成方法，捕捉传感器数据中的动态空间依赖关系。通过这种方式，它不依赖于预定义的邻接矩阵，使其适用于任何缺乏先验知识的情景。

为了充分考虑不同时间点道路网络的动态空间依赖关系，我们设计了一个时空嵌入生成器（STE generator）。生成器的核心过程找到与当前交通信号

X_{p}

对应的日内嵌入

T^{D}_{P}

和周内嵌入

T^{W}_{P}

。然后，将这些embedding和空间embedding

进行逐元素乘法运算，得到一个新的时空嵌入

E^{st}_{P}

，具体表述如下：

E^{st}_{P}=E\odot T^{D}_{P}\odot T^{W}_{P}

其中，

T^{D}_{P},T^{W}_{P}\in R^{P \times N \times D}

分别表示时间步

P=[t-P+1,...,t]

的日内，周内embedding，

\odot

表示逐元素乘法运算(Element-wise*Multiplication)*。

在时间步

，当前时间步的输入通过一个MLP层，以提取动态信号：

F_{t}=MLP(x_{t})

F_{t}\in R^{N \times D}

表示经过滤波后得到的动态信号。然后，在

F_{t}

和

E^{st}_{t}

上执行逐元素乘法运算，生成动态图embedding，表达如下：

E^{d}_{t}=tanh(F_{t}\odot E^{st}_{t})

接下来，根据节点相似性来生成图，可以通过将

E^{d}_{t}

和

{E^{d}_{t}}^{T}

相乘来推断空间依赖关系。然后，为了满足切比雪夫多项式的要求，生成的动态矩阵进行如下归一化：

D_{t}^{-\frac{1}{2}}A^{d}_{t}D_{t}^{-\frac{1}{2}}=D_{t}^{-\frac{1}{2}}(ReLU(E^{d}_{t}{E^{d}_{t}}^{T}))D_{t}^{-\frac{1}{2}}

其中，

A^{d}_{t}\in R^{N \times N}

代表时间步 t 的动态图。这将代入GCN公式，得到动态卷积公式，表达如下：

\begin{aligned} Z_{t}&=(I_{N}+D_{t}^{-\frac{1}{2}}A^{d}_{t}D_{t}^{-\frac{1}{2}})X+b\\ &=(I_{N}+D_{t}^{-\frac{1}{2}}(ReLU(E^{d}_{t}{E^{d}_{t}}^{T}))D_{t}^{-\frac{1}{2}})X+b \end{aligned}

4.2 Node adaptive parameter learning

GCN通过一个称为节点自适应参数学习（NAPL）模块进行优化。基于矩阵分解，该模块允许模型为每个节点学习自身独特的交通模式。在这里，权重矩阵被设置为

\theta \in R^{N \times c \times F}

。然后，为了优化GCN并防止过拟合，将权重矩阵分解为节点参数矩阵，以及两个权重矩阵

W_{g}\in R^{d \times c \times F}

和

b_{g} \in R^{d \times F}

，其中

d<=N

且

\theta = E_{g}W_{g}

b= E_{g}b_{g}

。优化后的GCN公式如下：

Z=(I_{N}+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})XE_{g}W_{g}+E_{g}b_{g}

4.3 Dynamic graph convolution recurrent module

为了捕获交通数据中复杂的时间相关性。我们采用GRU来捕获时空特征。我们将GRU中的矩阵乘法替换为动态图卷积方法和NAPL模块的组合，得到了一种动态图卷积门控循环单元（DGCRU）。DGCRU可以表示如下：

\begin{aligned} r_{t}&=\theta[x_{t}\parallel H_{t-1},DE]EW_{r}+Eb_{r}\\ u_{t}&=\theta[x_{t}\parallel H_{t-1},DE]EW_{u}+Eb_{u}\\ c_{t}&=tanh(\theta[x_{t}\parallel r_{t} \odot H_{t-1},DE]EW_{c}+Eb_{c})\\ H_{t}&=u_{t}\odot H_{t-1} +(1-u_{t})\odot c_{t} \end{aligned}

其中，

x_{t}

和

H_{t}

分别是时间步的输入和输出，

\theta

代表动态图生成，

\parallel

代表连接操作。

W_{r},W_{u},W_{c}

和

b_{r},b_{u},b_{c}

是可学习的参数。

由DGCRU组成的DGCRM用于从交通信号序列中提取时空特征。最后一个DGCRU的隐藏状态

H_{P}

被视为DGCRM的输出

H^{l}

。

4.4 Residual decomposition and multi-step prediction

为了实现多步预测和信号分解，该框架在DGCRM之后包括一个由线性层组成的输出子层。该输出子层有两个输出：

\begin{aligned} \hat{y}^{l}&=Linear_{l,f}(H^{l})\\ x^{l}_{b}&=Linear_{l,b}(H^{l}) \end{aligned}

预测输出

\hat{y}^{l} \in R^{Q \times N \times C}

表示通过第

l^{th}

块对

x^{l}

进行

的预测，而反向预测输出

x^{l}_{b} \in R^{P \times N \times C}

表示通过对第

l^{th}

块对

x^{l}

进行反向预测。模型的最终输出为：

\begin{aligned} y&=\sum_{n}^{l} \hat{y}^{l}\\ x^{l+1}_{P}&=x^{l}_{P}-x^{l}_{b} \end{aligned}

反向预测可以被视为交通信号分解的过程。具体而言，

x^{l}_{b}

*可以被看作是输入信号

x^{l}_{P}

的重构，其中包含了

H^{l}

从

x^{l}_{P}

*学到的信息。通过残差分解，从

x^{l}_{P}

中学到的信息被移除，仅保留下一个块中尚未学到的部分

x^{l+1}_{P}

以用于下一个块中的建模。最终每个块的输出值相加形成最终的预测值。

4.5 Segmented learning training strategy

虽然采用信号分解的方式有效的提高了模型的准确性，该方法需要叠加多层才能发挥作用，这通常会导致训练模型所需的时间和GPU等硬件要求大大增加。受到 MTGNN 和 DGCRN的启发，我们基于模型预测分解的特点设计了一种有效的训练策略，称为分段学习(Segmented learning training strategy)。在训练的早期阶段，只训练前 L 个层，而不是所有层一起训练。随着训练的深入，我们逐步将未训练的层添加到训练中去(换句话说，我们一开始就训练一层，等第一层训练的差不多了，我们将第二层放进去一起训练，以此反复操作)。因此，这种训练方式大大减少了训练初期所需的时间和内存。分段学习方案的概述可在算法1中找到。

5 实验

5.1 数据集

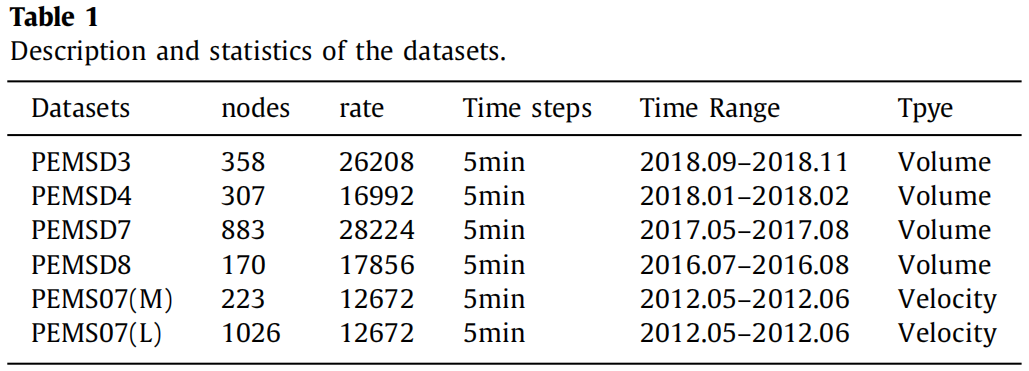
5.2 预测性能比较

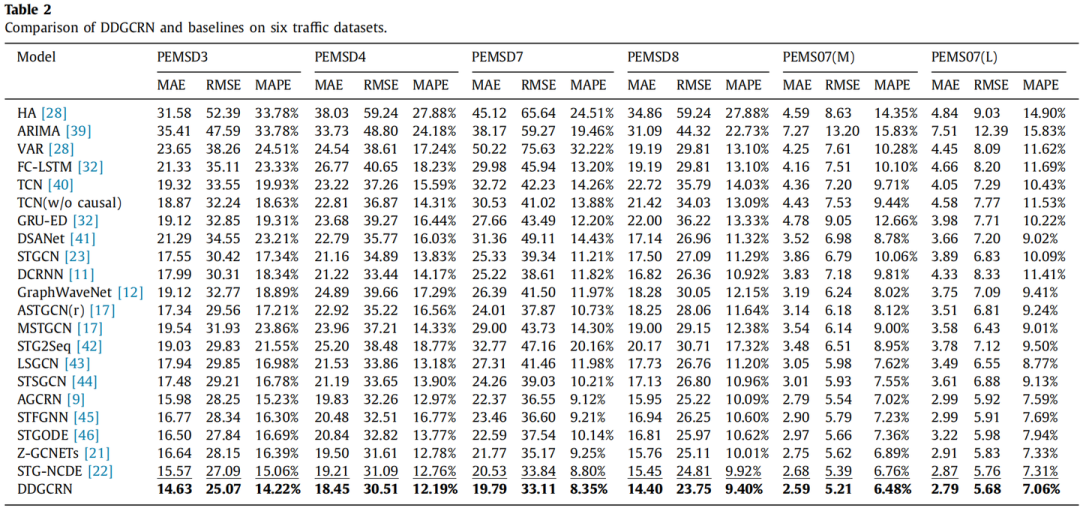
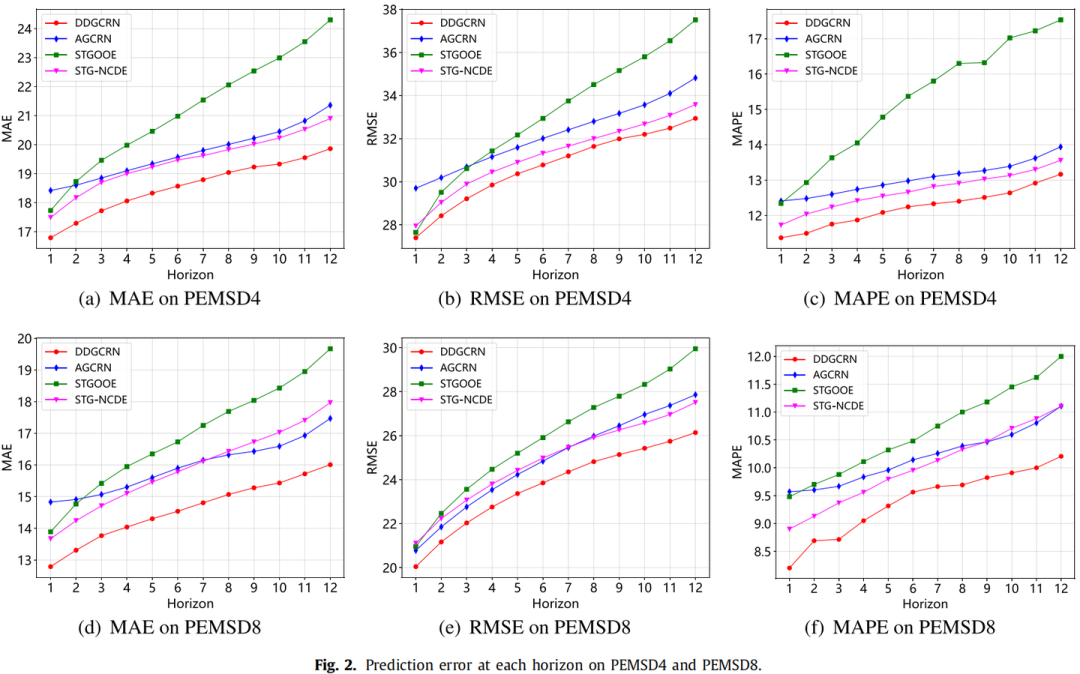
从效果来看，DDGCRN在各个数据集上的性能都达到了SOTA。

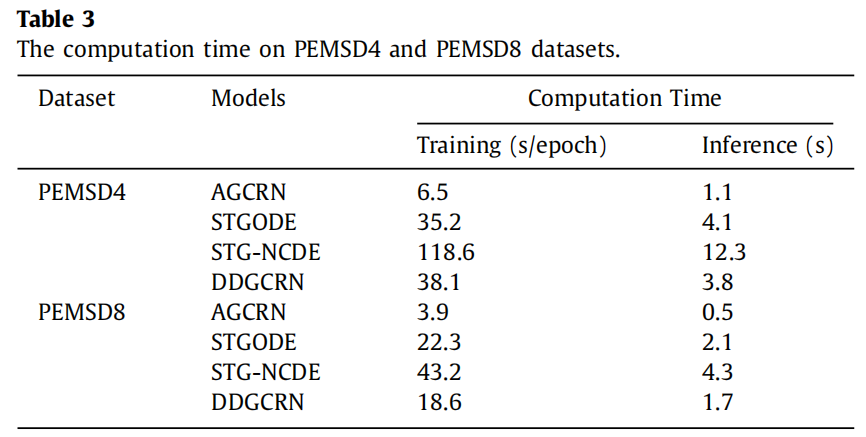
5.3 计算开销

在效率方面，DDGCRN和STGODE的计算成本相同，仅次于AGCRN。然而，其准确性比其他基线要好得多。由于其简单的自适应图构造方法，AGCRN的计算速度最快，但由于它不考虑时间点和动态变化，它的分数不如STG-NCDE好。STG-NCDE工作得很好，但由于它使用常微分方程（Odes）进行建模，因此它的计算时间相对较长，因此它的速度和效率远低于DDGCRN。

6 消融实验

6.1 模块消融分析

为了验证各模块的有效性，我们设计了以下变体来验证不同模型组合的效果：

w/o DG: 消除动态图，仅使用节点自适应参数学习模块进行建模。该变体测试了动态图卷积的贡献。
w/o SL: 不使用分段学习策略训练模型。该变体旨在测试学习策略是否影响模型性能。
w/o NA: 消除节点自适应参数学习模块，仅使用基本矩阵乘法操作。该变体测试了节点自适应参数学习模块的贡献。

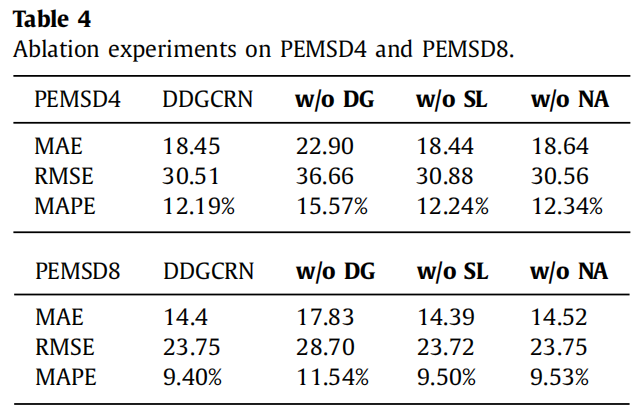
如图所示，DDGCRN远优于w/o DG，说明动态图在该框架中起着积极的作用。w/o SL的表现与DDGCRN相似，这表明分段学习可以在不影响模型性能的情况下减少内存需求和训练时间。最后，w/o NA的性能不如DDGCRN，证明了节点自适应参数学习模块对DDGCRN的整体性能有坚实的贡献。

6.2 不同类型的图结构的效果分析

为了验证不同类型的图结构对模型效果的影响。我们设计以下四种变体来证明动态图的必要性：

DDGCRN-dg: 这是带有动态图卷积的DDGCRN。
DDGCRN-ag: 用AGCRN中的自适应图替换动态图。
DDGCRN-c: 使用附加到数据集的处理过的邻接矩阵作为图卷积的预定义图。预定义图的相邻节点之间的权重都设为1，并进行拉普拉斯矩阵归一化。
DDGCRN-d: 该变体使用节点表示的传感器之间距离的倒数作为边的权重。

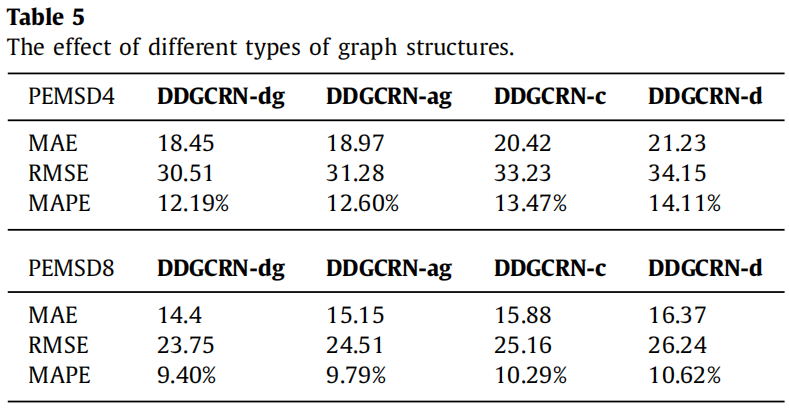
DDGCRN-dg和DDGCRN-ag的表现明显优于其他变体，这证明了人工设计的预定义图在表示交通网络的空间相关性方面的局限性。DDGCRN-dg优于DDGCRN-ag的性能也表明，交通路况不是固定不变的，因此要通过考虑路网的动态变化来改善。此外，DDGCRN-c的性能明显优于DDGCRN-d，这也表明，即使图的结构相同，不合理的权重设计也会极大地影响图的卷积。这也证明了人工构造的图结构的局限性。

6.3 节点自适应参数（NAPL）学习模块实用性分析

为测试NAPL模块的实用性，设计了三个不同的模块变体：

use NA: 这是使用NAPL模块的DDGCRN。
use ND: 该变体使用节点动态参数学习模块。其相应的GCN公式为：

Z^{t}=(I_{N}+D^{-\frac{1}{2}}_{t}A^{d}_{t}D^{-\frac{1}{2}}_{t})X^{t}E^{d}_{t}W_{g}+E^{d}_{t}b_{g}

该模块将动态参数学习模块中的节点嵌入

替换为动态图嵌入

E^{d}_{t}

，以实现动态调整。

no NA: 该变体不使用节点自适应参数学习模块。相反，它仅使用最简单的线性乘法进行图卷积。

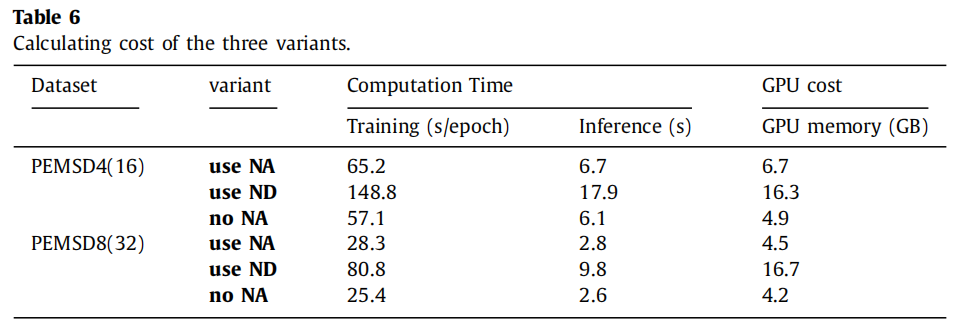
从表6可以看出，use NA和no NA所需的体所需的计算时间和GPU成本差距不大。然而，use ND的计算时间和GPU成本比其他两个变体要大得多。这是因为节点动态参数学习模块在其过程中生成了一个五维张量，大大增加了模型的复杂性。由于这导致了如此高的资源需求，不利于实际部署模型。

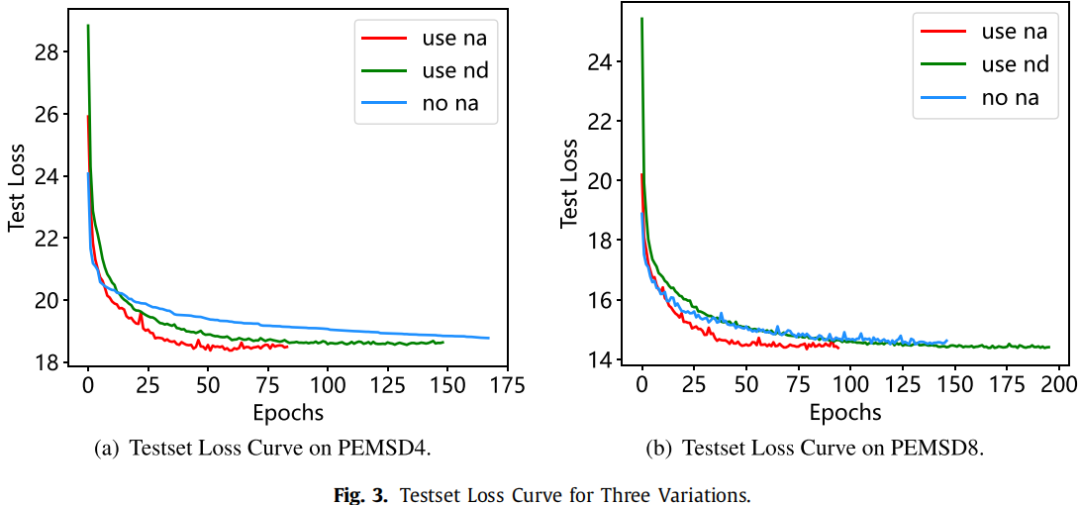
图3比较了PEMSD4和PEMSD8数据集的测试集损失曲线。尽管损失曲线在早期阶段迅速下降，但no NA的准确性不如use NA或use ND}。此外，尽管use ND的准确性与use NA相当，但其损失曲线下降较慢。事实上，use ND需要的周期数是use NA的两倍，才能达到峰值准确性。此外，use ND的每个epoch的训练时间超过use NA的两倍。因此，use ND通过训练达到相同性能水平所需的时间是use NA的三到四倍。这是不划算的。总体而言，use NA以较低的成本和更快的训练速度达到最佳性能。因此，我们选择使用NAPL模块优化GCN。

6.4 可视化

为了进一步展示不同时间点和不同日期的交通路况的空间相关性的区别，我们使用几个时间点在不同日内的时空embedding进行可视化来展示效果。我们选取对应时间点0点、6点、12点、18点的日embedding，以及对应周三、周四、周六、周日的周embedding来生成对应的时空embedding。为了方便可视化，我们使用t-SNE将时空embedding的维度降维到2维。

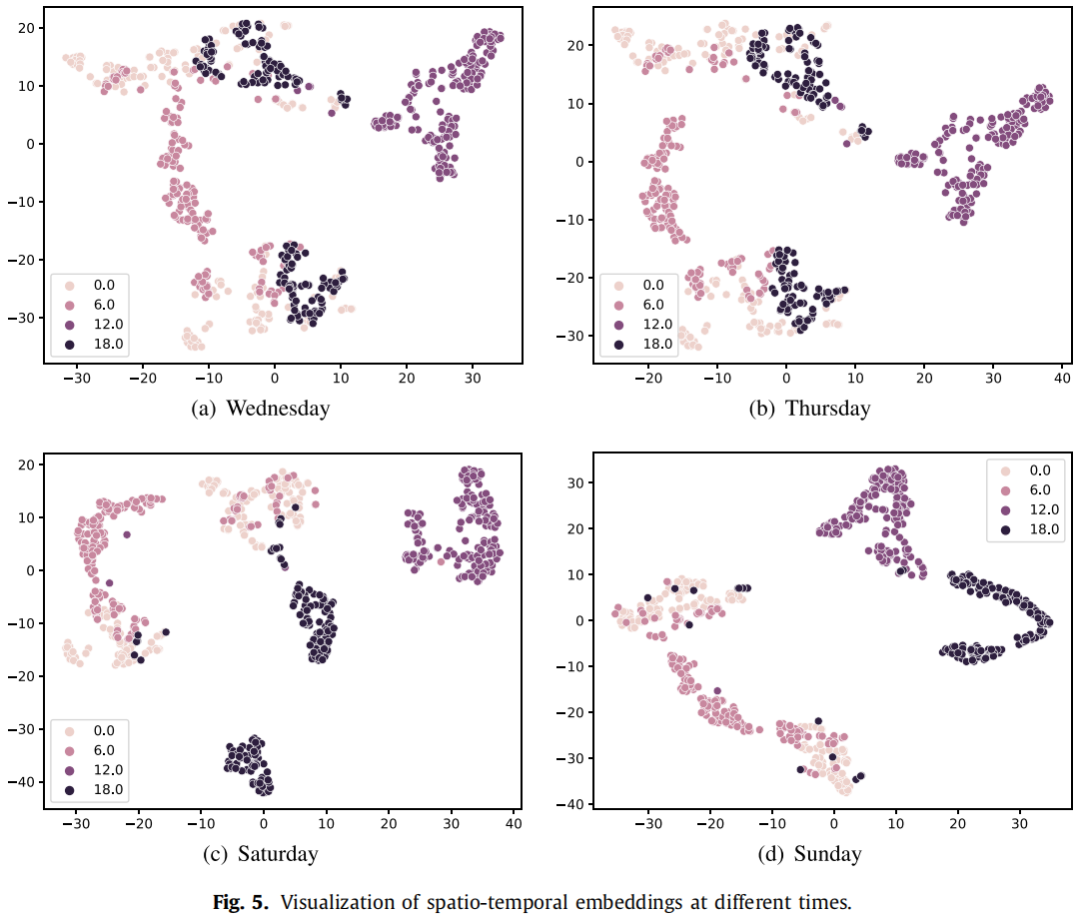
从图5中可以看出，每个时间点的embedding都有明显的聚类。在星期三和星期四，许多0:00和18:00的embedding聚类在一起，表明它们的交通状况相似。然而，周六和周日就不是这样了，这主要是由于工作日与周末的差异导致的。此外，12:00的嵌入在工作日和周末都不与其他时间点聚类在一起。这与实际的交通状况相一致，即在交通状况通常在12:00时比较拥堵，而在其他时间相对较为顺畅。

7 总结

本文提出了一种新的交通预测分解动态图模型DDGCRN。该模型利用时空嵌入和交通信号来生成动态图。其中DGCRM模块负责捕获时空相关性，同时残差分解机制被用来从正常信号中分离出异常信号。此外，文章还提出了一种新的分段学习训练策略，以显著减少初始训练所需的时间和资源。在6个数据集上进行的广泛实验中，DDGCRN始终优于其他方法。

DDGCRN提出的动态图生成方法取得了优异的性能，减少了对先验知识的依赖，进一步提高了时空图的通用性。然而，尽管其优越的性能，仍有改进的空间。例如，DDGCRN只是简单地将交通信号分解为正常信号和异常信号进行建模。如果可以对交通信号中的多个交通模式进行分解以进行建模，则可以进一步提高模型的性能和可解释性。