【机器学习】分而知变，积而见道：微积分中的世界之思

半截诗

发布于 2025-01-09 17:29:59

31700

代码可运行

文章被收录于专栏：学西学西

运行总次数：0

代码可运行

微积分基础：理解变化与累积的数学

💬 欢迎讨论：如果你在阅读过程中有任何疑问或想要进一步探讨的内容，欢迎在评论区留言！我们一起学习、一起成长。 👍 点赞、收藏与分享：如果你觉得这篇文章对你有帮助，记得点赞、收藏并分享给更多想了解机器学习的朋友！ 🚀 开启微积分之旅：微积分是理解变化和累积的数学工具，是机器学习中的重要基础。让我们一起深入探索微积分的核心概念，打好数学基础，为后续的机器学习学习做好准备。

前言

在机器学习的学习旅程中，微积分作为支撑理论之一，是理解模型优化与变化规律的关键。无论是在梯度下降、损失函数优化，还是在复杂模型的训练过程中，微积分都有着举足轻重的作用。在之前的博客中，我们已经介绍了线性代数和概率论的基础，这些都为进一步的学习奠定了基础。今天，我们将深入讲解微积分基础，特别是在机器学习中的应用。

如果你是机器学习的初学者，或者希望加强自己在微积分方面的基础知识，今天的内容将帮助你理解一些核心概念，并为后续更复杂的学习打下坚实的基础。

一、微积分概述与基础概念

1.1 微积分的定义与重要性

微积分是数学的一个分支，主要研究变化率（微分）和累积量（积分）。它在科学、工程、经济学以及机器学习等领域中有广泛的应用。

1.1.1 微积分的基本组成

微分学（Differential Calculus）：研究函数的变化率，主要涉及导数的概念。
积分学（Integral Calculus）：研究函数的累积量，主要涉及积分的概念。

1.1.2 微积分在机器学习中的应用

梯度下降优化：利用导数计算损失函数的梯度，以更新模型参数。
损失函数的最小化：通过微积分方法找到损失函数的最小值，从而优化模型性能。
概率密度函数的积分：在概率模型中，积分用于计算概率分布的期望值和方差。

1.2 微积分的历史与发展

微积分的发展历史悠久，主要由艾萨克·牛顿（Isaac Newton)和戈特弗里德·莱布尼茨（Gottfried Wilhelm Leibniz）在17世纪独立发展起来。

牛顿：主要用于物理学中的运动和力的研究。
莱布尼茨：发展了微积分的符号表示法，如积分符号

\int

和微分符号

。

随着时间的推移，微积分在数学中的地位不断提升，并成为现代科学和工程的基础工具之一。

二、极限与连续性

2.1 极限的定义与计算

极限是微积分的基石，描述了函数在某一点附近的行为。

2.1.1 极限的直观理解

当变量趋近于某个值时，函数的输出趋近于一个特定的数值，这个数值就是函数在该点的极限。

2.1.2 极限的数学定义

函数

f(x)

在

x = a

处的极限是

，记作：

\lim_{x \to a} f(x) = L

2.1.3 极限的计算方法

直接代入法：如果

f(x)

在

x = a

处连续，则：

\lim_{x \to a} f(x) = f(a)

因式分解法：用于消除分母中的零，或约去公因式。
洛必达法则（L’Hospital’s Rule）：当极限形式为

\frac{0}{0}

或

\frac{\infty}{\infty}

时，可以对分子和分母分别求导，然后再求极限。

2.1.4 实例：计算极限

示例 1：计算

\lim_{x \to 2} \frac{x^2 - 4}{x - 2}

解答：直接代入

x = 2

得到

\frac{0}{0}

的不定形式，需进行因式分解：

\frac{x^2 - 4}{x - 2} = \frac{(x - 2)(x + 2)}{x - 2} = x + 2

因此：

\lim_{x \to 2} (x + 2) = 4

示例 2：计算

\lim_{x \to 0} \frac{\sin(x)}{x}

解答：使用洛必达法则：

\lim_{x \to 0} \frac{\sin(x)}{x} = \lim_{x \to 0} \frac{\cos(x)}{1} = 1

2.2 连续性的定义与性质

连续性描述了函数在某一点没有“跳跃”或“断裂”的性质。

2.2.1 连续函数的定义

函数

f(x)

在

x = a

处连续，当且仅当满足以下三个条件：

f(a)

存在。

\lim_{x \to a} f(x)

存在。

\lim_{x \to a} f(x) = f(a)

2.2.2 间断点的类型

可去间断点（Removable Discontinuity）：极限存在但不等于函数值，或函数值未定义。
跳跃间断点（Jump Discontinuity）：左右极限存在但不相等。
无穷间断点（Infinite Discontinuity）：极限为正无穷或负无穷。

2.2.3 连续性的性质

四则运算：若

f(x)

和

g(x)

在

x = a

处连续，则

f(x) + g(x)

、

f(x) - g(x)

、

f(x) \times g(x)

和

\frac{f(x)}{g(x)}

（当

g(a) \neq 0

）在

x = a

处连续。

复合函数：若

f(x)

在

x = a

处连续，且

g(x)

在

y = f(a)

处连续，则

g(f(x))

在

x = a

处连续。

2.2.4 实例：连续性判断

示例 1：判断函数

f(x) = \frac{x^2 - 1}{x - 1}

在

x = 1

处是否连续。

解答：简化函数：

f(x) = \frac{(x - 1)(x + 1)}{x - 1} = x + 1 \quad \text{（当 } x \neq 1 \text{ 时）}

在

x = 1

处：

\lim_{x \to 1} f(x) = 2

若定义

f(1) = 2

，则

f(x)

在

x = 1

处连续；否则，是可去间断点。

2.3 实战项目：使用Python绘制函数的极限与连续性示意图

通过实战项目，我们将使用Python绘制函数在某一点的极限与连续性的示意图，帮助直观理解这些概念。

2.3.1 项目目标

绘制函数

f(x) = \frac{x^2 - 4}{x - 2}

在

x = 2

处的极限示意图。

标注函数在

x = 2

处的连续性情况。

2.3.2 Python代码实现

import numpy as np
import matplotlib.pyplot as plt

# 定义函数 f(x) = (x^2 - 4)/(x - 2), x != 2
def f(x):
    return (x**2 - 4)/(x - 2)

# 定义简化后的函数 g(x) = x + 2, x != 2
def g(x):
    return x + 2

# 生成 x 值，避开 x = 2
x = np.linspace(1, 3, 400)
x = x[x != 2]
y = f(x)
y_simplified = g(x)

# 绘制函数
plt.figure(figsize=(8, 6))
plt.plot(x, y, label=r'$f(x) = \frac{x^2 - 4}{x - 2}$', color='blue')
plt.plot(x, y_simplified, '--', label=r'$g(x) = x + 2$', color='red')

# 标注 x = 2
plt.axvline(x=2, color='gray', linestyle='--')
plt.scatter(2, 4, color='green', zorder=5, label=r'$f(2) = 4$')

# 设置图例和标签
plt.legend(fontsize=12)
plt.xlabel(r'$x$', fontsize=12)
plt.ylabel(r'$f(x)$', fontsize=12)
plt.title(r'函数 $f(x)$ 和其简化形式 $g(x)$ 的示意图', fontsize=14)
plt.grid(True)

# 显示图表
plt.show()

2.3.3 运行结果

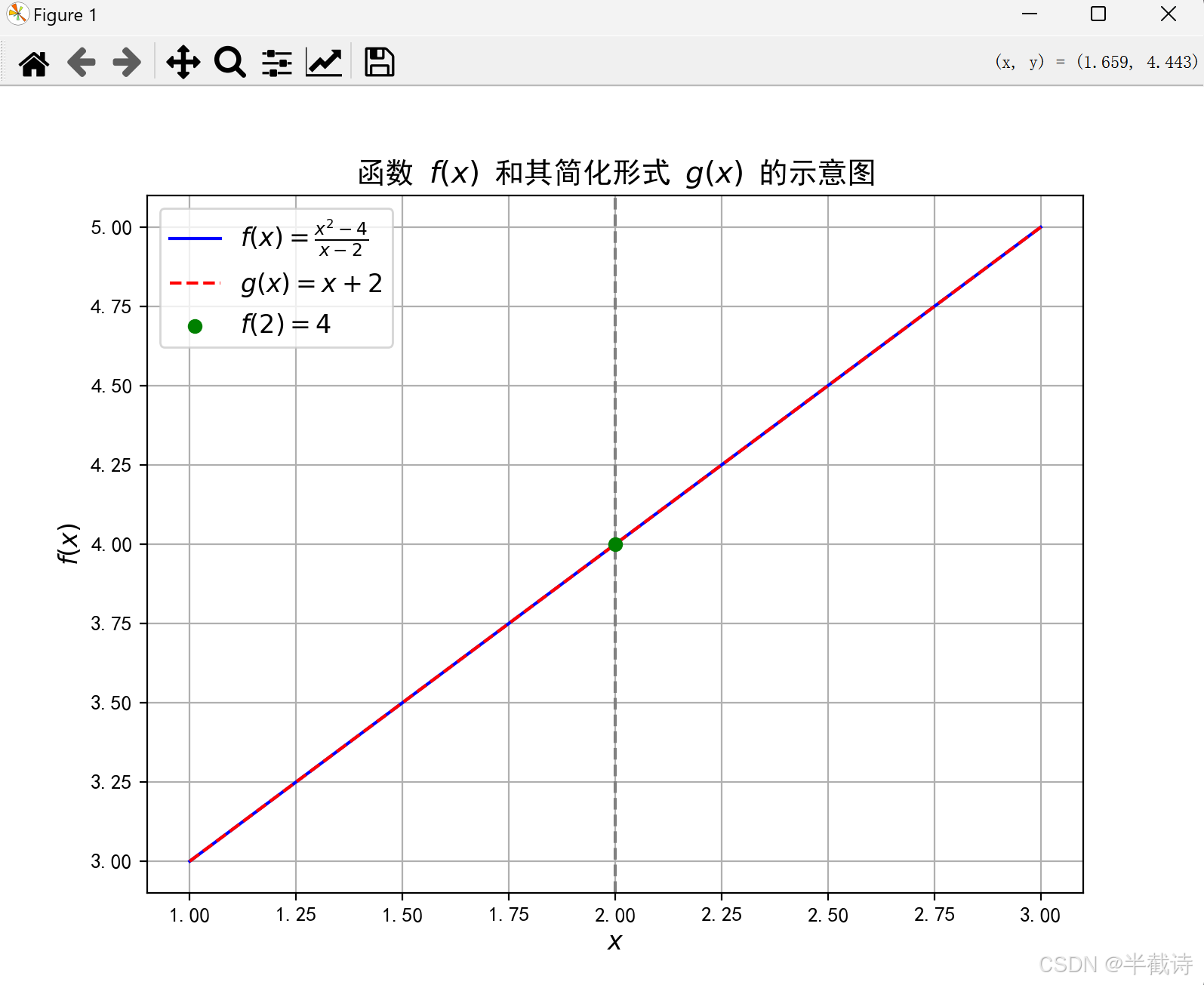
2.3.4 结果解读

函数

f(x)

：在

x = 2

处存在一个可去间断点，函数值为4。

简化后的函数

g(x) = x + 2

：是

f(x)

的连续扩展，消除了分母为零的问题。

图中标注：绿色点表示

f(2) = 4

，显示了在

x = 2

处函数的定义和值。

通过这个示意图，我们可以直观地看到函数在某一点的极限与连续性情况。

三、导数的概念与计算

3.1 导数的定义

导数是微积分的核心概念之一，描述了函数在某一点的瞬时变化率。

3.1.1 导数的几何意义

导数表示函数在某一点处的切线斜率，即函数在该点的瞬时变化率。

3.1.2 导数的物理意义

在物理学中，导数用于描述速度、加速度等瞬时变化量。例如，位置函数的导数是速度函数，速度函数的导数是加速度函数。

3.1.3 导数的数学定义

函数

f(x)

在点

x = a

处的导数定义为：

f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h}

如果这个极限存在，则称

f(x)

在

x = a

处可导。

3.2 导数的计算规则

3.2.1 基本导数法则

常数法则：

\frac{d}{dx}c = 0

其中，

是常数。

幂函数法则：

\frac{d}{dx}x^n = n x^{n-1}

其中，

是常数。

指数函数法则：

\frac{d}{dx}e^x = e^x

\frac{d}{dx}a^x = a^x \ln(a)

其中，

是正数常数。

对数函数法则：

\frac{d}{dx}\ln(x) = \frac{1}{x}

\frac{d}{dx}\log_a(x) = \frac{1}{x \ln(a)}

三角函数法则：

\frac{d}{dx}\sin(x) = \cos(x)

\frac{d}{dx}\cos(x) = -\sin(x)

\frac{d}{dx}\tan(x) = \sec^2(x)

3.2.2 乘积法则与商法则

乘积法则（Product Rule）：

\frac{d}{dx}[u(x) \cdot v(x)] = u'(x) \cdot v(x) + u(x) \cdot v'(x)

商法则（Quotient Rule）：

\frac{d}{dx}\left[\frac{u(x)}{v(x)}\right] = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{v(x)^2}

3.2.3 链式法则（Chain Rule）

当函数是复合函数时，使用链式法则进行求导：

\frac{d}{dx}f(g(x)) = f'(g(x)) \cdot g'(x)

3.3 实例：简单导数计算

3.3.1 示例 1：多项式函数的导数

问题：计算函数

f(x) = 3x^4 - 5x^2 + 6x - 2

的导数。

解答：应用幂函数法则：

f'(x) = 12x^3 - 10x + 6

3.3.2 示例 2：指数函数的导数

问题：计算函数

g(x) = e^{2x}

的导数。

解答：应用指数函数法则和链式法则：

g'(x) = 2e^{2x}

3.3.3 示例 3：商函数的导数

问题：计算函数

h(x) = \frac{\sin(x)}{x}

的导数。

解答：应用商法则：

h'(x) = \frac{\cos(x) \cdot x - \sin(x) \cdot 1}{x^2} = \frac{x \cos(x) - \sin(x)}{x^2}

3.4 实战项目：使用SymPy库进行符号导数计算并绘制导数曲线

通过实战项目，我们将使用Python的SymPy库进行符号导数计算，并绘制函数及其导数的曲线，帮助直观理解导数的概念。

3.4.1 项目目标

计算函数

f(x) = x^3 - 4x + 1

的导数。

绘制函数

f(x)

和其导数

f'(x)

的曲线。

标注导数在不同点的值，展示函数的增长与减少趋势。

3.4.2 Python代码实现

import numpy as np
import matplotlib.pyplot as plt
import sympy as sp

# 定义符号变量
x = sp.symbols('x')

# 定义函数 f(x) = x^3 - 4x + 1
f = x**3 - 4*x + 1

# 计算导数 f'(x)
f_prime = sp.diff(f, x)

# 将符号表达式转换为数值函数
f_func = sp.lambdify(x, f, 'numpy')
f_prime_func = sp.lambdify(x, f_prime, 'numpy')

# 生成 x 值
x_vals = np.linspace(-3, 3, 400)
y_vals = f_func(x_vals)
y_prime_vals = f_prime_func(x_vals)

# 绘制函数和导数曲线
plt.figure(figsize=(10,6))
plt.plot(x_vals, y_vals, label='f(x) = x³ - 4x + 1', color='blue')
plt.plot(x_vals, y_prime_vals, label="f'(x) = 3x² - 4", color='red', linestyle='--')

# 标注关键点
critical_points = sp.solve(f_prime, x)
for point in critical_points:
    y_cp = f_func(point)
    y_prime_cp = f_prime_func(point)
    plt.scatter(point, y_cp, color='green')
    plt.annotate(f'({point:.2f}, {y_cp:.2f})', (point, y_cp),
                 textcoords="offset points", xytext=(0,10), ha='center')

# 设置图例和标签
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('函数 f(x) 及其导数 f\'(x) 的曲线')
plt.grid(True)
plt.show()

3.4.3 运行结果

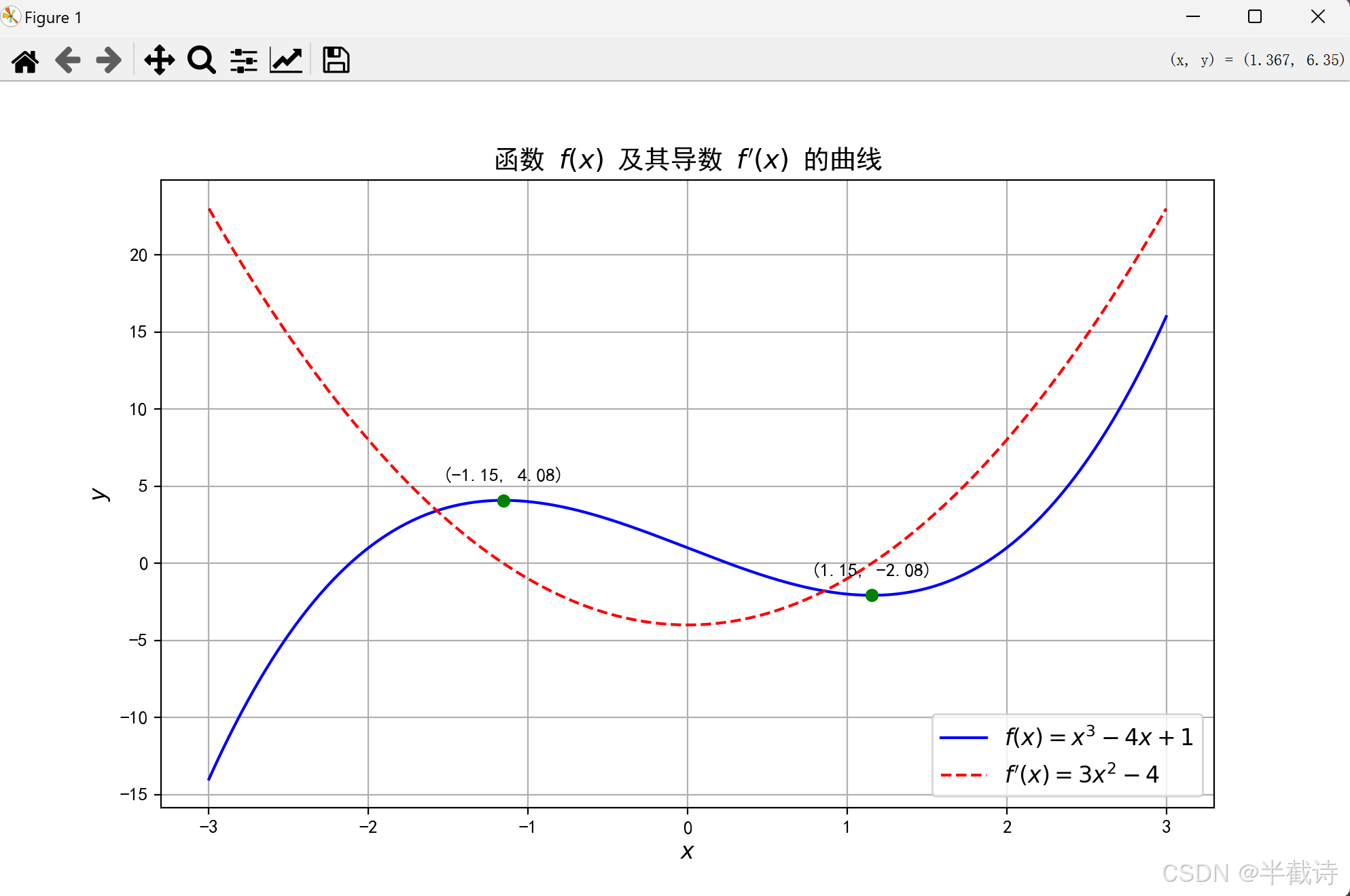
3.4.4 结果解读

函数

f(x) = x^3 - 4x + 1

：

蓝色实线表示原函数的曲线。

导数

f'(x) = 3x^2 - 4

：

红色虚线表示函数的导数曲线，展示了函数在各点的变化率。

关键点标注：
- 绿色点表示函数的临界点，即导数为零的点。
- 这些点对应函数的极大值和极小值，展示了函数的增长和减少趋势。

通过这个示意图，我们可以直观地看到函数在不同点的变化率，以及导数在优化中的重要作用。

四、导数的应用：优化与变化

4.1 优化问题的数学表述

在机器学习中，优化问题是核心任务之一。优化的目标是找到使得某个目标函数（如损失函数）最小化或最大化的参数值。

4.1.1 优化问题的标准形式

\min_{\theta} J(\theta)

其中：

\theta

表示模型的参数。

J(\theta)

表示目标函数，通常是损失函数。

4.1.2 导数在优化中的作用

导数提供了目标函数在某一点的变化率信息，帮助我们理解目标函数的趋势，从而指导参数更新的方向和步长。

4.2 梯度下降法

梯度下降法是最常用的优化算法之一，旨在通过迭代更新参数，逐步逼近目标函数的最小值。

4.2.1 梯度的定义

梯度是目标函数对参数的偏导数组成的向量，表示目标函数在参数空间中的上升最快方向。

\nabla J(\theta) = \left[ \frac{\partial J}{\partial \theta_1}, \frac{\partial J}{\partial \theta_2}, \dots, \frac{\partial J}{\partial \theta_n} \right]

4.2.2 梯度下降的更新规则

\theta := \theta - \alpha \nabla J(\theta)

其中：

\alpha

是学习率，控制每次更新的步长。

\nabla J(\theta)

是目标函数在当前参数

\theta

处的梯度。

4.2.3 梯度下降的类型

批量梯度下降（Batch Gradient Descent）：
- 使用整个训练集计算梯度，适用于小型数据集。
随机梯度下降（Stochastic Gradient Descent, SGD）：
- 每次使用一个样本计算梯度，适用于大型数据集。
小批量梯度下降（Mini-Batch Gradient Descent）：
- 每次使用一小部分样本计算梯度，结合了批量和随机梯度下降的优点。

4.3 实例：梯度下降法在简单模型中的应用

通过实战项目，我们将实现一个简单的线性回归模型，并使用梯度下降法优化模型参数。

4.3.1 项目目标

建立一个线性回归模型

y = \theta_0 + \theta_1 x

。

使用梯度下降法最小化均方误差（Mean Squared Error, MSE）。
可视化损失函数的下降过程。

4.3.2 Python代码实现

import numpy as np
import matplotlib.pyplot as plt

# 生成模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)  # y = 4 + 3x + Gaussian noise

# 添加 x0 = 1 到每个实例（截距项）
X_b = np.c_[np.ones((100, 1)), X]  # X_b.shape = (100, 2)

# 初始化参数 theta = [theta0, theta1]
theta = np.random.randn(2, 1)

# 梯度下降参数
learning_rate = 0.1
n_iterations = 1000
m = 100  # 样本数量

# 存储损失值
loss_history = []

for iteration in range(n_iterations):
    # 计算梯度
    gradients = 2 / m * X_b.T.dot(X_b.dot(theta) - y)
    # 更新参数
    theta = theta - learning_rate * gradients
    # 计算当前的损失（均方误差）
    loss = (1 / m) * np.sum((X_b.dot(theta) - y) ** 2)
    loss_history.append(loss)

# 输出优化后的参数
print(f"优化后的 theta0（截距）: {theta[0][0]:.2f}")
print(f"优化后的 theta1（斜率）: {theta[1][0]:.2f}")

# 绘制损失函数下降曲线
plt.figure(figsize=(8, 6))
plt.plot(range(n_iterations), loss_history, color='purple')
plt.xlabel('迭代次数', fontsize=12)
plt.ylabel('均方误差 (MSE)', fontsize=12)
plt.title('梯度下降优化过程中的损失变化', fontsize=14)
plt.grid(True)
plt.show()

# 绘制数据与回归线
plt.figure(figsize=(8, 6))
plt.scatter(X, y, color='blue', label='数据点')
plt.plot(X, X_b.dot(theta), color='red', label='拟合的回归线')
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title('线性回归模型与数据点', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()

4.3.3 运行结果

优化后的theta0（截距）: 4.22
优化后的theta1（斜率）: 2.97

4.3.4 结果解读

优化后的参数：
\theta_0 \approx 4.22
\theta_1 \approx 2.97
这接近于数据生成时的真实参数

\theta_0 = 4

，

\theta_1 = 3

，表明梯度下降法成功地最小化了损失函数。

损失函数下降曲线：
- 显示了均方误差随着迭代次数的增加而逐步下降，最终趋于稳定，表明优化过程收敛。

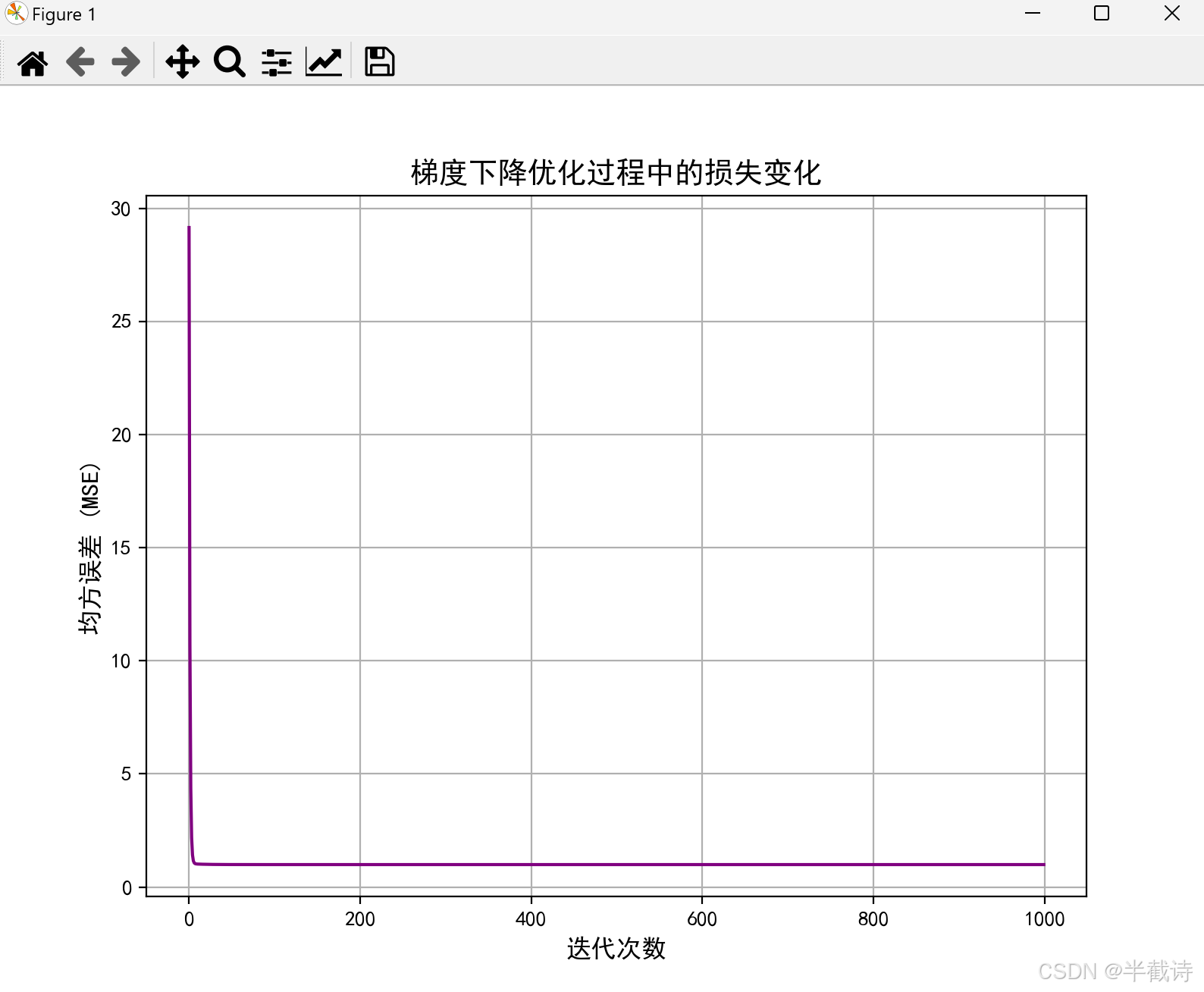
线性回归模型与数据点：
- 红色回归线很好地拟合了蓝色数据点，验证了模型的有效性。

通过这个实战项目，我们深入了解了梯度下降法在优化模型参数中的应用，以及如何通过可视化手段监控优化过程。

五、总结与展望

本篇，我们从微积分的视角重新审视了变化与累积的关系。通过对极限、连续性、导数的深入讲解，以及梯度下降法在优化中的应用，我们不仅掌握了微积分的基本概念和计算方法，还理解了微积分在机器学习中的关键作用。微积分，是我们理解模型优化与变化规律的数学基石，它为我们在后续学习更复杂的机器学习算法提供了坚实的理论支持。小结：

极限与连续性帮助我们理解函数在某一点的行为与性质。
导数描述了函数的瞬时变化率，是优化算法中的关键工具。
梯度下降法利用导数信息，指导模型参数的优化过程。

展望：在接下来的博客中，我们将继续深入学习微积分的其他重要概念，如积分，并探讨其在机器学习中的具体应用。通过系统化的学习，你将逐步构建起扎实的数学知识体系，为后续的机器学习算法与模型的理解与实现打下坚实的基础。希望通过本系列的学习，你能逐步掌握微积分的核心知识，提升在机器学习领域的分析与建模能力。

以上就是关于【机器学习】分而知变，积而见道：微积分中的世界之思的内容啦，各位大佬有什么问题欢迎在评论区指正，或者私信我也是可以的啦，您的支持是我创作的最大动力！❤️

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2024-12-22，如有侵权请联系 cloudcommunity@tencent.com 删除

基础

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度