一致性哈希算法的权衡

半吊子全栈工匠

发布于 2025-10-11 12:52:54

9000

代码可运行

运行总次数：0

代码可运行

一致性哈希（Consistent Hashing）是一种特殊的哈希算法，主要用于解决分布式系统中节点动态变化时的数据分布问题。它在保持数据分布均匀的同时，尽量减少节点加入或离开时需要重新分配的数据量。一致性哈希算法在许多场景下都非常有用，例如在缓存系统、负载均衡器、数据库分片等应用中。

1.一致性哈希解决的问题

问题：

有一个键值对的集合，还有一些用于键值存储的服务器例如 memcached，Redis，MySQL等等。在没有全局存储目录的条件下，如何把Key发布到不同服务器上，然后可以找到它。

2. 那些一致性哈希算法

2.1 模N哈希

首先，选择一个哈希函数来将键(字符串)映射为一个整数。这往往排除了像 SHA-1或 MD5这样的加密算法，因为其计算成本较高。MurmurHash 以及 xxHash等非加密哈希函数都是不错的选择。

如果您有 N 个服务器，您可以使用 hash 函数散列密钥，并取得结果的整数模 N。 server := serverList[hash(key) % N]

这种设置很容易解释, 计算成本很低。如果 N 是2的幂，那么只需要比特掩码即可。

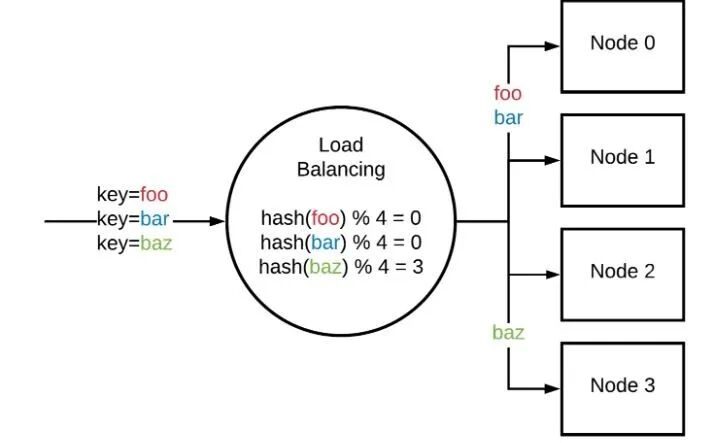
但是，局限也是显然的。模N哈希难以应对服务器的数量变化。理想的哈希函数当面临添加或删除一个服务器时，应该只移动1/n的键，不需要移动的键不要移动。

2.2 环哈希

环哈希（ring-based consistent hashing）的基本思想是，每个服务器被映射到一个具有哈希函数的圆上的一个点，可以把圆看作所有的整数0,1,2......2^32-1 的集合。要查找给定键的服务器，需要对该密钥执行散列并在圆上找到该点。然后向前扫描，直到找到任何服务器的第一个哈希值。实际上，每个服务器会在哈希环上出现多次。这些额外的点称为“虚拟节点”或“ vnode”。这减少了服务器之间的负载差异。对于少量的 vnode，不同的服务器可以分配不同数量的键。

Ketama 是一个 memcached 客户段，它使用环哈希来跨服务器实例的键分布。一个ketama算法的go 语言参考实现如下：

func (c Continuum) Hash(thing string) string {

    if len(c.ring) == 0 {
        return ""
    }

    h := hashString(thing)

    var i uint
    switch c.hash {
    case HashFunc1:
        i = search(c.ring, h)
    case HashFunc2:
        i = uint(sort.Search(len(c.ring), func(i int) bool { return c.ring[i].point >= h }))
        if i >= uint(len(c.ring)) {
            i = 0
        }
    }

    return c.ring[i].bucket.Label
}

环哈希算法很简单。为了查看给定键存储在哪个节点上，键被哈希为一个整数。搜索已排序的节点，以查找大于键哈希的最小节点，然后在映射中查找该节点哈希值，以确定它来自哪个节点。

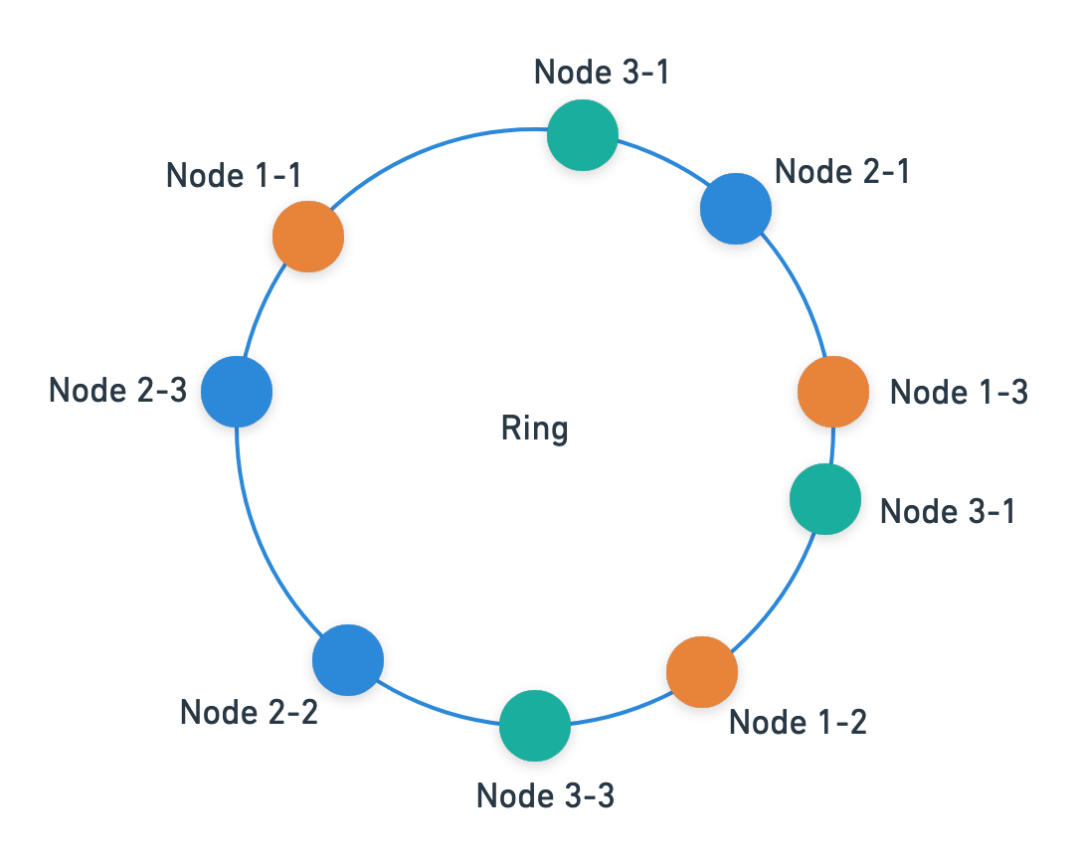
但是，即便使用了环哈希算法，节点之间的负载分布仍然是不均匀的。例如，每台服务器有100个副本，负载标准差约为10% 。桶大小的99% 置信区间是平均负载(即键总数/服务器数量)的0.76至1.28。这种可变性使容量规划变得棘手。如果将每台服务器的副本数量增加到1000个节点，标准差减少到3.2% ，而99% 的置信区间减少到0.92到1.09。这需要大量的内存消耗。对于1000个节点，几乎要4 MB 的数据，O (log n)搜索也会面临大量的缓存未命中情况。

2.3 跳跃哈希

跳跃哈希（Jump Hashing）克服了环哈希的缺点: 它没有内存开销，实际上是完美的密钥分发。桶的标准差为0.00000764% ，99%的置信区间为0.9999998至1.00000002。

跳跃哈希的go语言参考实现如下：

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
    int64_t b = -1, j = 0;
    while (j < num_buckets) {
        b = j;
        key = key * 2862933555777941757ULL + 1;
        j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
    }
    return b;
}

跳跃哈希也很快。循环执行 O (ln n)次，比环哈希的 O (log n)二分查找快一个常量，甚至更快，计算完全在几个寄存器中完成，不需要支付缓存未命中的开销。该算法使用键的哈希值作为随机数生成器的种子。然后，它使用随机数字在桶列表中“跳转”，最后的一个桶是结果。

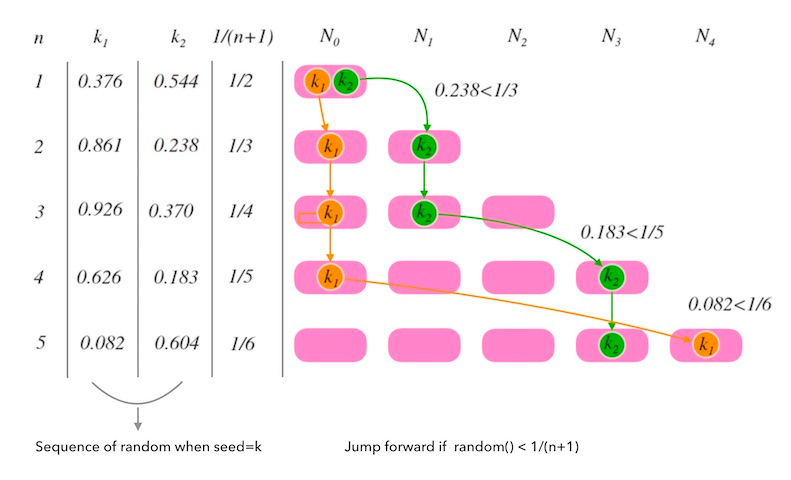
跳跃哈希的主要限制是它只返回范围为桶数量-1的整数，且不支持任意的桶名。如果使用环哈希，即使两个不同的实例以不同的顺序接收它们的服务器列表，得到的密钥映射仍然是相同的。使用跳跃哈希的一个方法是提供一个节点编号，而不是服务器名称。其次，它只能正确地添加和删除范围上端的节点，这意味着它不支持任意节点删除。例如，不能使用它在 memcached 实例集中分发键，因为其中一个实例可能会崩溃，而无法从可能的目的列表中删除崩溃的节点。

环哈希提供了任意桶的添加和删除能力，但代价是使用高内存以减少负载差异。跳转哈希提供了有效的完美负载分割，但是在更改节点计数时降低了灵活性。

2.4 多探测器一致性哈希

多探测器一致性哈希（Multi-Probe Consistent Hashing）的基本思想是，不要对节点进行多次哈希处理，使内存使用量增加，而是只对节点进行一次哈希处理，但在查找时对键进行 k 次哈希处理，并返回所有查询中最接近的节点。K 值由期望的方差决定。

一个多探测器一致性哈希算法的go 语言参考实现如下：

// Hash returns the bucket for a given key
func (m *Multi) Hash(key string) string {
    bkey := []byte(key)

    minDistance := uint64(math.MaxUint64)

    var minhash uint64

    h1 := m.hashf(bkey, m.seeds[0])
    h2 := m.hashf(bkey, m.seeds[1])

    for i := 0; i < m.k; i++ {
        hash := h1 + uint64(i)*h2
        prefix := (hash & m.prefixmask) >> m.prefixshift

        var node uint64
    FOUND:
        for {
            uints := m.bhashes[prefix]

            for _, v := range uints {
                if hash < v {
                    node = v
                    break FOUND
                }
            }

            prefix++
            if prefix == uint64(len(m.bhashes)) {
                prefix = 0
                // wrapped -- take the first node hash we can find
                for uints = nil; uints == nil; prefix++ {
                    uints = m.bhashes[prefix]
                }

                node = uints[0]
                break FOUND
            }
        }

        distance := node - hash
        if distance < minDistance {
            minDistance = distance
            minhash = node
        }
    }

    return m.bmap[minhash]
}

多探测器一致性哈希提供 O (n)空间(每个节点一个条目) ，以及 O (1)添加和删除节点，局限时查找变慢了。

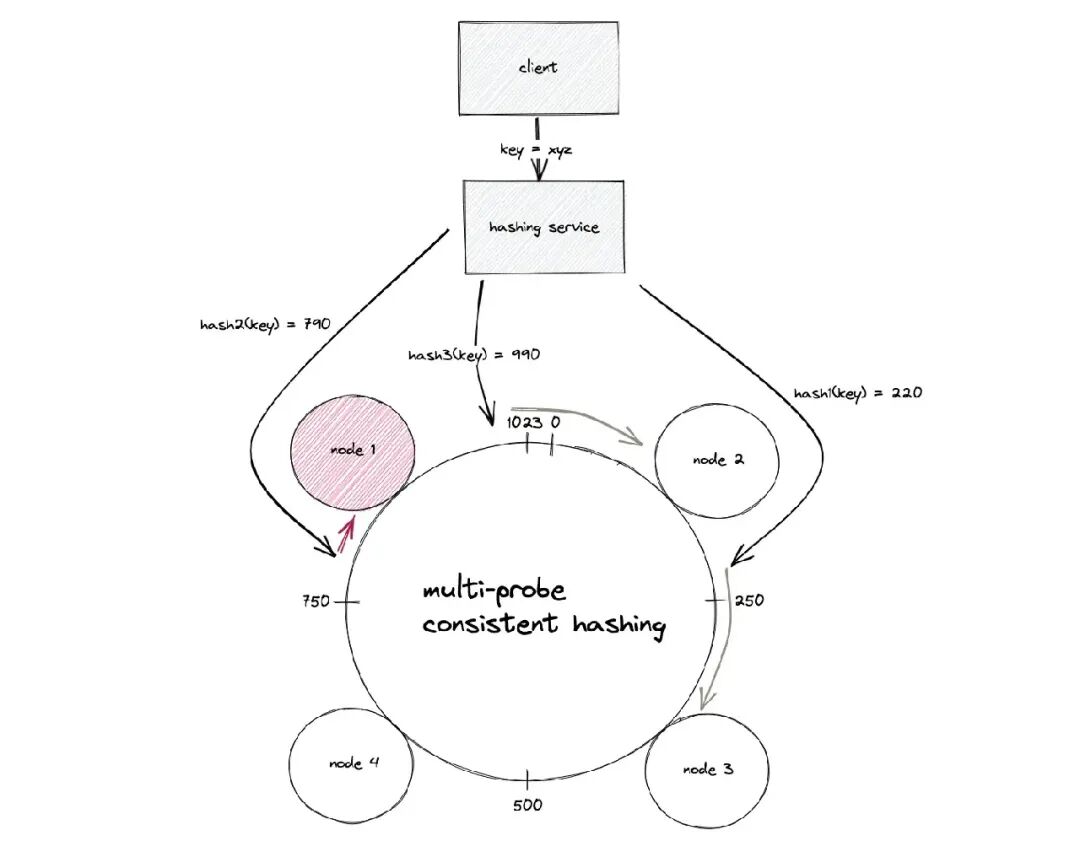
对于1.05的峰均比，这意味着负载最重的节点最多比平均值高5%)，k 为21。使用复杂的数据结构，可以得到从 O (k logn)到 O (k)的总查找成本。作为对比，要使环哈希的等效峰均比为1.05，每个节点需要700 ln n 副本。对于100个节点，这意味着超过一兆字节的内存。

2.5 交会哈希

交会哈希（Rendezvous Hashing）也叫最高随机权哈希，其基本思想是将节点和键在一起执行哈希函数，并使用提供最高哈希值的节点。

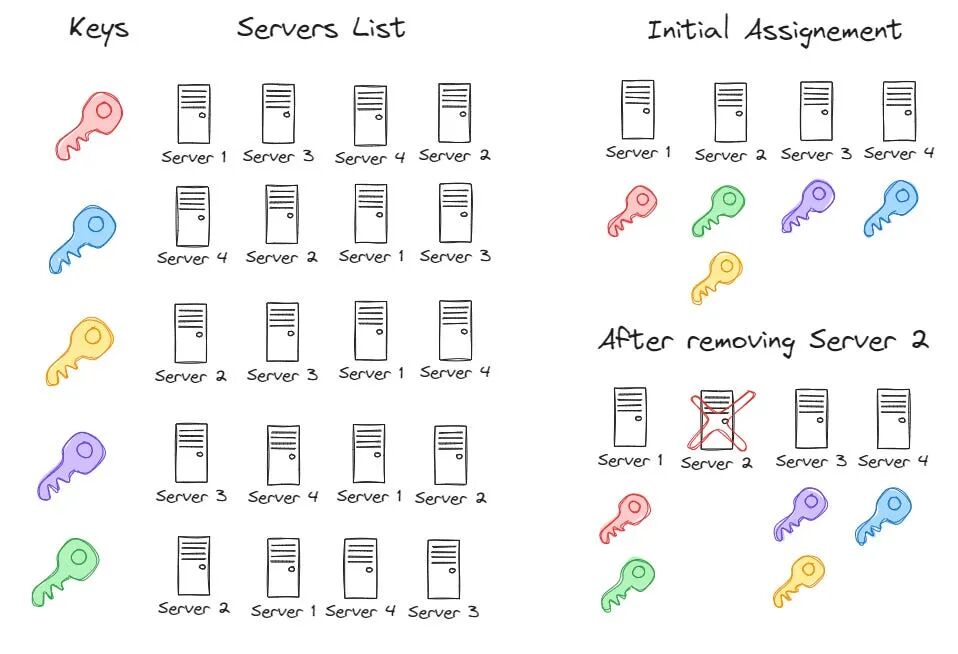
其缺点是很难避免遍历所有节点的 O (n)查找开销。以下是来自go语言实现的查找示例：

func (r *Rendezvous) Lookup(k string) string {
    khash := r.hash(k)

    var midx int
    var mhash = xorshiftMult64(khash ^ r.nhash[0])

    for i, nhash := range r.nhash[1:] {
        if h := xorshiftMult64(khash ^ nhash); h > mhash {
            midx = i + 1
            mhash = h
        }
    }

    return r.nstr[midx]
}

即使交会哈希的查找复杂的是 O (n)，内部循环也没有那么昂贵。根据节点的数量，它可以很容易地实现“足够快”。

2.6 磁悬浮哈希

磁悬浮哈希（Maglev Hashing）源自谷歌，其中一个主要目标是与环哈希或交会哈希相比，拥有较快查找速度和较低的内存使用。该算法有效地生成了一个查找表，允许在恒定的时间内查找节点。这样做的两个缺点是生成一个关于节点故障的新表的速度很慢，这也有效地限制了后端节点的最大数量。

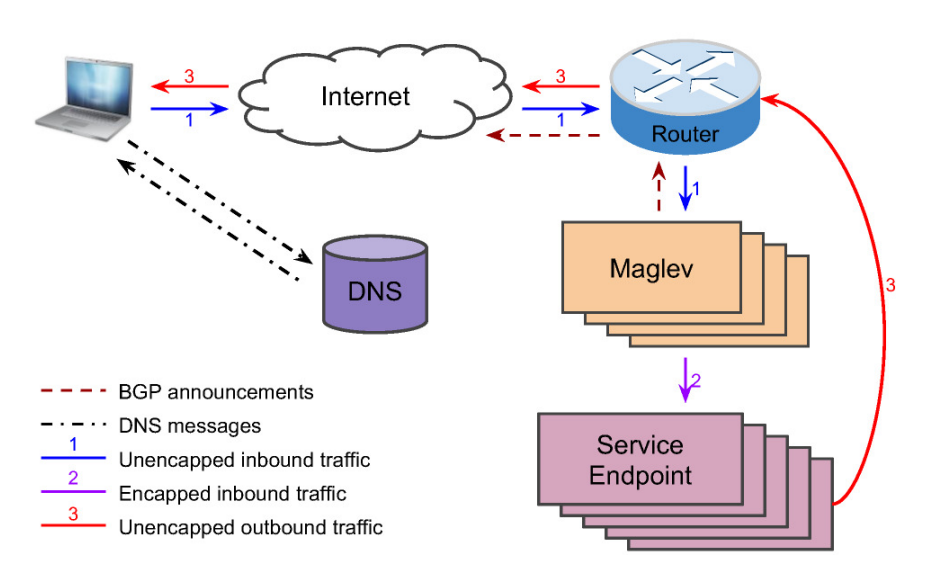
磁悬浮哈希的另一个目标是在添加和删除节点时实现“最小干扰”，而不是优化。对于磁悬浮哈希作为软件负载平衡器的场景来说，这就足够了。

磁悬浮哈希中关于构造查找表的go语言参考实现如下：

func New(names []string, m uint64) *Table {
    offsets, skips := generateOffsetAndSkips(names, m)
    t := &Table{
        n:              len(names),
        skips:          skips,
        currentOffsets: offsets,
        originOffsets:  make([]uint64, len(names)),
        m:              m,
    }

    // save first currentOffsets to originOffsets, for reset
    copy(t.originOffsets, t.currentOffsets)
    t.lookup = t.populate(m, nil)

    return t
}

查找表实际上是节点的随机排列。查找对键进行哈希运算，并检查该位置的条目。这是带有一个小常量的 O (1)复杂度，只是对键执行哈希的时间。

主流的一致性哈希算法的对比如下：

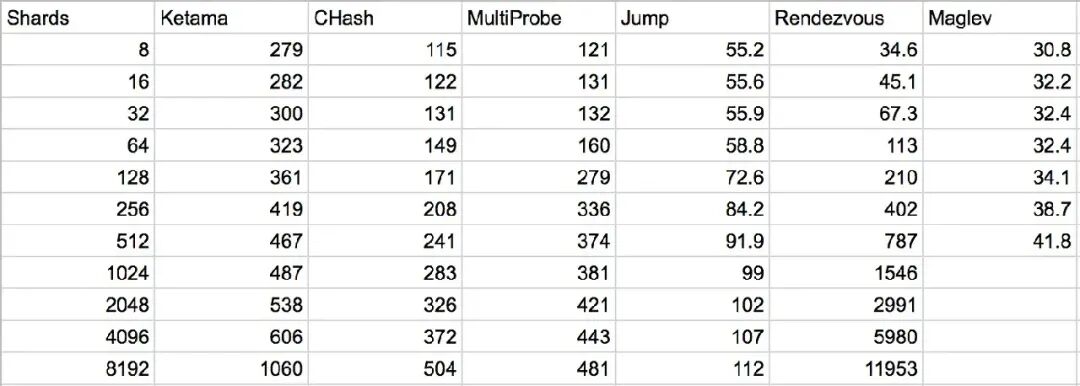
3. 一致性哈希的典型应用场景

一致性哈希算法一般应用在分布式系统之中。在分布式系统中，机器节点和数据都很多，节点可能会频繁地增加或故障宕机，导致数据无法取得。为了解决这个问题，出现了使用一致性哈希算法来规划数据的存放节点的方法。

3.1 服务副本

分布式系统中的服务副本使用一致性哈希算法来为给定的键选择辅助(或更多)节点。这可以是为了防止节点故障，也可以仅作为第二个节点进行查询以减少延迟。有些策略使用完整的节点复制，即每个服务器有两个完整的副本，而其他策略则跨服务器复制键。

我们总是能够以可预测的方式变更键或键的哈希，并执行完整的第二次查找，但也需要注意在同一个节点上的副本键。

有些算法可以直接选择多个节点进行备份或复制。对于环哈希，使用传递到圆上的下一个节点; 对于多探针一致性哈希，使用下一个最接近的节点。交会哈希采取下一个最高(或最低)的节点。跳跃哈希是有点棘手，但它也是可以做到的。

同样，选择复制策略也充满了权衡。

3.2 加权主机

在添加具有不同权重的服务器方面，一致哈希算法的简单性和有效性各不相同。也就是说，将更多(或更少)负载发送到一个服务器，而不是发送给其他服务器。使用环哈希，可以按照所需的负载缩放副本的数量，但这会极大地增加内存使用。

跳跃哈希和多探测器一致性哈希在使用和维持现有的性能保证方面更加棘手。虽然总是可以添加引用原始节点的第二个“影子”节点，但是当负载倍数不是整数时，此方法将失效。一种方法是按一定数量缩放所有节点计数，但这会增加内存和查找时间。

磁悬浮哈希通过改变表的构造过程来获得权重，这样权重较大的节点可以更频繁地在查找表中选择条目。

加权交会哈希用于为交会哈希算法添加权重，即选择按权重比例缩放的最高组合哈希。

3.3 负载均衡

使用一致性哈希进行负载平衡是一个很有吸引力的想法。但根据算法的不同，这最终可能不会比随机分配好，随机分配会导致分布不平衡。

除了磁悬浮哈希之外，还有两种一致哈希的负载平衡方法。

一个是基于有界负载的一致性哈希算法。由于键分布在服务器之间，因此会检查负载，如果某个节点已经负载过重，则跳过该节点。这种算法可以到 HAProxy 的复杂均衡器上，也可以作为一个独立的软件包使用。

对于选择连接到哪些后端的客户端而言，谷歌提出了一种称为“确定性的子设置”的算法，在其SRE book 中有详细信息。

4. 一句话小结

一致性哈希算法都在努力平衡键的分布、内存使用、查找时间和构建时间(包括节点添加和删除成本)。只有权衡，没有完美的一致性哈希算法。

如果大家对更多的算法工程实践感兴趣的话，欢迎阅读笔者和几位朋友的最新译作——《算法工程珠玑》，会给大家带来对算法落地的有益实践。

【参考资料与关联阅读】

文中代码主要源自 https://github.com/dgryski/
https://www.akamai.com/es/es/multimedia/documents/technical-publication/consistent-hashing-and-random-trees-distributed-caching-protocols-for-relieving-hot-spots-on-the-world-wide-web-technical-publication.pdf
“A Fast, Minimal Memory, Consistent Hash Algorithm”，https://arxiv.org/abs/1406.2294
“Multi-Probe Consistent Hashing”，https://arxiv.org/abs/1505.00062
“A name-Based Mapping scheme for Rendezvous”，https://www.eecs.umich.edu/techreports/cse/96/CSE-TR-316-96.pdf
“Maglev: A Fast and Reliable Software Network Load Balancer”，https://research.google.com/pubs/pub44824.html
"Consistent Hashing with Bounded Loads", https://research.googleblog.com/2017/04/consistent-hashing-with-bounded-loads.html
有向无环图（DAG）的温故知新
DHT算法的一知半解
算法与模型的浅析
大模型应用框架：LangChain与LlamaIndex的对比选择
从Docker 网络看IaC
机器学习模型性能的10个指标
大模型应用设计的10个思考
解读大模型的微调
一文读懂“语言模型”
难以捉摸？机器学习模型的可解释性初探
大模型应用的10种架构模式
全网首发：MCP 的10种架构模式
7B？13B？175B？解读大模型的参数
全网首发：安全性问题，使MCP成为AI应用的双刃剑，如何化险为夷呢？
“提示工程”的技术分类
大模型系列：提示词管理
提示工程中的10个设计模式
解读：基于图的大模型提示技术
Chunking：基于大模型RAG系统中的文档分块