一步直接封神！单步扩散媲美250步教师模型！中科大&字节发布图像生成“分层蒸馏术”

作者：Hanbo Cheng等

解读：AI生成未来

文章链接：https://arxiv.org/pdf/2511.08930

亮点直击

• 系统性分析与统一视角：对轨迹蒸馏（TD）进行了系统性分析，揭示了其本质是一种有损压缩过程。这一视角解释了为何TD方法虽然能有效保留全局结构，却不可避免地会牺牲精细细节。
• 创新的分层蒸馏框架：重新审视轨迹蒸馏和分布蒸馏的角色，提出一个新颖的分层蒸馏（Hierarchical Distillation, HD）框架。该框架协同利用两种方法的优势，先构建结构，再优化细节。
• 专为细节优化的判别器：为配合HD框架，设计了自适应加权判别器（Adaptive Weighted Discriminator, AWD），一种新颖的对抗机制，专为优化高质量生成器的局部瑕疵而设计，从而显著提升最终生成质量。

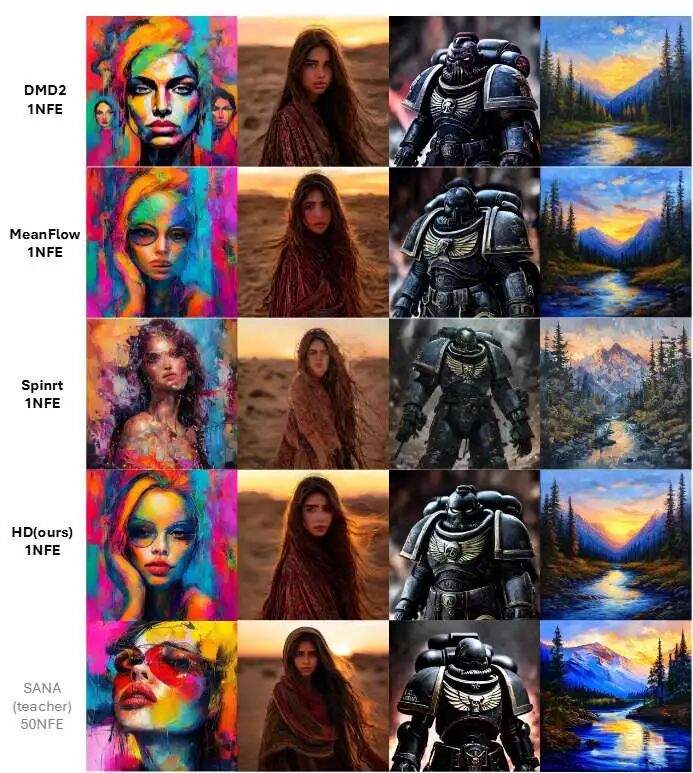
图 1.50 步教师 SANA和我们的 1 步高清方法的生成质量比较。本文方法达到了与多步骤教师相当的质量。

图 1.50 步教师 SANA和我们的 1 步高清方法的生成质量比较。本文方法达到了与多步骤教师相当的质量。

解决的问题

本文旨在解决扩散模型推理延迟过高的问题，特别是在单步或少步生成场景下。现有的加速方法主要分为两类：

1. 轨迹蒸馏（Trajectory-based Distillation, TD）：此类方法能很好地保留生成内容的全局结构，但由于其“有损压缩”的特性，会牺牲高频细节，导致保真度下降。
2. 分布蒸馏（Distribution-based Distillation）：此类方法理论上可以达到更高的保真度，但常常受困于模式崩溃（mode collapse）和训练不稳定的问题，尤其是在初始分布不佳的情况下。 本文的工作旨在克服这两类方法的固有缺陷，将它们的优势结合起来，实现高保真、高效率的单步生成。

提出的方案

本文提出了一个名为分层蒸馏（Hierarchical Distillation, HD）的两阶段框架，其核心思想是“先搭骨架，再填血肉”。

• 第一阶段：结构化初始化
  • 利用基于轨迹蒸馏的方法（具体采用MeanFlow），将一个多步教师模型的结构先验知识“注入”到学生模型中。
  • 此阶段的目标不是生成最终结果，而是为学生模型提供一个结构合理、接近真实数据流形的“草图”或高质量的初始分布。这有效稳定了后续的训练过程。
• 第二阶段：分布优化
  • 将第一阶段预训练好的模型作为生成器，进行分布匹配（Distribution Matching, DM）的微调。
  • 此阶段引入对抗性训练来恢复在第一阶段丢失的高频细节并避免模式崩溃。
  • 为解决传统判别器在面对高质量生成器时难以提供有效监督信号的问题，本文设计了自适应加权判别器（AWD）。AWD通过注意力机制动态地为特征图上的不同空间位置（token）分配权重，使判别器能更专注于局部瑕疵，从而为生成器的细节优化提供更精准的指导。

应用的技术点

• 轨迹蒸馏（Trajectory Distillation, TD）：以MeanFlow作为实现方式，用于第一阶段的结构化初始化。
• 分布匹配蒸馏（Distribution Matching Distillation, DMD）：用于第二阶段的细节优化，旨在将生成分布与真实数据分布对齐。
• 对抗性训练（Adversarial Training）：在第二阶段引入，以稳定训练并减轻模式崩溃问题。
• 自适应加权判别器（Adaptive Weighted Discriminator, AWD）：本文提出的核心技术之一，通过可学习的查询嵌入（query embedding）和注意力机制来动态加权特征，从而聚焦于局部伪影的判别。

达到的效果

本文的方法在多个任务上均取得了当前最优（SOTA）的性能。

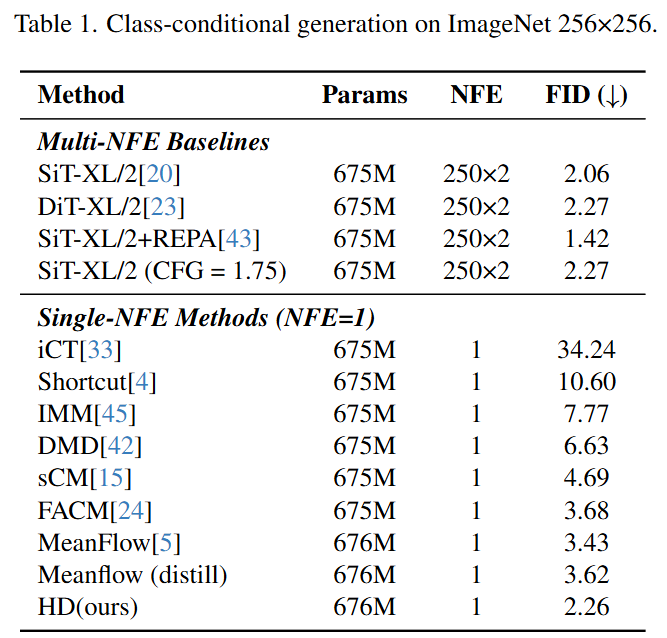
• 在ImageNet 256×256的类条件生成任务上，本文的单步模型达到了2.26的FID分数，这一成绩不仅在单步模型中领先，甚至可以媲美其250步的教师模型（FID为2.27）。
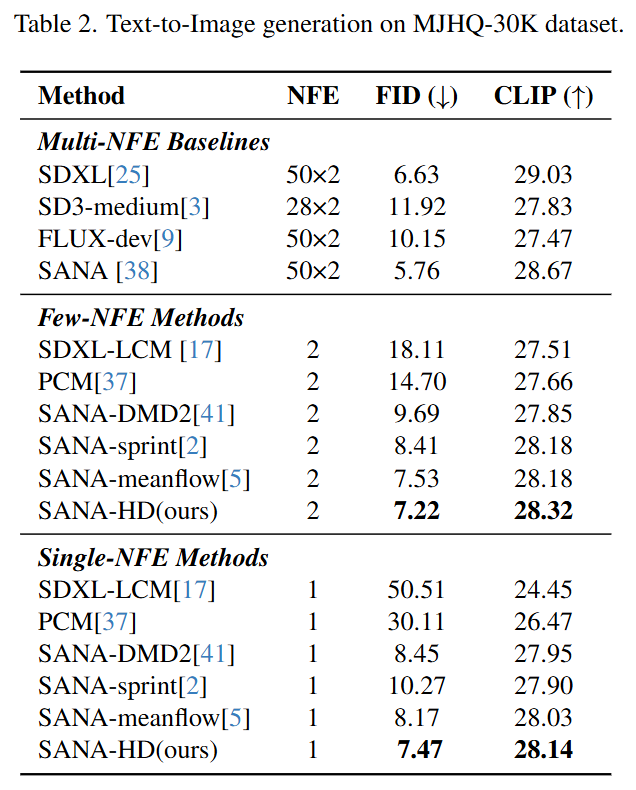
• 在MJHQ-30K高分辨率文生图基准测试上，单步和两步模型的FID和CLIP分数均优于现有的其他蒸馏方法，证明了其强大的泛化能力。

方法

本节介绍分层蒸馏（HD）框架的技术细节首先进行理论分析，统一主流的轨迹蒸馏（TD）方法，揭示它们共同的局限性，以此作为我们方法的动机。随后，详细介绍我们流水线的第一阶段，其中基于MeanFlow的TD阶段为学生模型注入了强大的结构先验。最后，描述了第二阶段，在这一阶段，对这个良好初始化的模型应用分布匹配，对其进行优化以实现高保真度的结果。

轨迹蒸馏的统一视角

本节进行理论分析以阐明轨迹蒸馏（TD）的建模目标。通过数学推导，证明了几种主流TD方法的目标，包括一致性模型（CM/sCM）和渐进式蒸馏（PGD），可以统一在平均速度估计的共同框架下。基于这一观察，识别出大多数TD方法固有的一个共同局限。

命题 1.连续一致性模型隐式地建模了区间 上的平均速度。

证明. 一致性模型的核心原则是强制网络输出 在任何给定的PF-ODE轨迹上保持一致性。这种一致性约束的微分形式可以表示为（详细推导见附录6）：

其中，在极限 时，这个离散关系产生了微分形式：

回想一下方程(5)中瞬时速度和平均速度之间的关系。具体来说，对于从 开始的区间，它变为：

这揭示了当 时，CM网络的输出 被隐式地训练来建模区间 上的平均速度，即 。

命题 2.随着蒸馏步骤数趋于无穷，渐进式蒸馏（PGD）收敛于对整个区间 上的平均速度进行建模。

证明. 渐进式蒸馏（PGD）是一个迭代过程，它在N轮中将一个 步的教师模型蒸馏成一个 步的学生模型。在每一轮 中，学生模型 被训练来预测其教师模型（）在两个连续时间步上的输出的平均值。

经过N轮蒸馏后，最终的单步学生模型 的输出可以表示为原始多步教师模型在 个离散时间步上的输出的算术平均值（详细推导见附录6）：

其中 是离散的时间步。原始的教师模型 被训练来近似瞬时速度，即 。当蒸馏轮数 时，该和收敛为一个积分：

根据定义，方程(13)的右侧是整个区间 上的平均速度 。这表明PGD也隐式地试图建模平均速度。

统一视角的影响. 统一分析产生了两个关键的见解，它们构成了我们所提出方法的理论基础。（1）我们的证明揭示了主流TD方法，无论其具体公式如何，都共享一个共同的本质：它们训练一个单一的神经网络 来近似一个动态的平均速度函数 。作为一个轨迹段上的积分，这个平均速度函数封装了来自多步教师模型PF-ODE路径的丰富高频动态信息。强迫一个有限容量的学生模型在单步中完美复制一个复杂的函数，从信息论的角度引入了一个根本性的瓶颈。这为所有单步TD方法都不可避免地遭受细粒度细节损失提供了理论解释。我们在5.1节中为这一主张提供了进一步的经验验证。（2）因为所有TD方法都共享建模平均速度这一基本目标，我们选择MeanFlow作为它们的代表性实现。这个决定不仅是基于其最先进的性能。更重要的是，MeanFlow明确且直接地对平均速度进行建模，提供了一个数学上优雅且稳健的实现。

第一阶段：通过TD进行结构化初始化

如前所述，从零开始应用分布匹配蒸馏（DMD）进行单步生成面临训练不稳定和模式崩溃的问题。一个主要原因是生成分布和真实数据分布之间缺乏重叠。为了解决这个问题，我们引入了一个结构化初始化阶段。利用轨迹蒸馏（TD）来有效地将多步教师模型积累的丰富结构先验注入到学生模型中。这确保了在分布匹配阶段开始之前，学生模型就已经具备了捕捉目标分布宏观结构和布局的强大能力。基于前面的分析，采用MeanFlow作为我们TD阶段的蒸馏目标。尽管MeanFlow最初是为从零开始训练模型而提出的，但我们认为将其重新用作蒸馏框架可以提供一个方差更低的学习信号。从零开始训练时，模型从数据和噪声的随机配对中学习，其中每个样本都呈现一个独特的、高方差的目标。相比之下，蒸馏利用了一个已经收敛到从噪声到数据的固定、确定性映射的预训练教师模型。来自教师的这种指导确保了学习目标在训练期间是一致的，从而降低了梯度信号的方-差，并导致一个更稳定和高效的初始化阶段。

图 2.分层蒸馏 (HD) 管道。我们的方法包括两个主要阶段：(1) 结构化初始化：基于 MeanFlow 的方法为学生灌输基础结构信息。(2) 分布细化：第二阶段采用专为 HD 框架设计的自适应加权判别器 (AWD)，恢复高频细节。SN "和 "LN "分别指谱规范[22]和层规范

图 2.分层蒸馏 (HD) 管道。我们的方法包括两个主要阶段：(1) 结构化初始化：基于 MeanFlow 的方法为学生灌输基础结构信息。(2) 分布细化：第二阶段采用专为 HD 框架设计的自适应加权判别器 (AWD)，恢复高频细节。SN "和 "LN "分别指谱规范[22]和层规范

这个阶段的流程图如图2的上半部分所示。在我们的蒸馏框架中，将（最初在标准MeanFlow中由线性插值导出的）真实瞬时速度场 替换为预训练教师模型 的输出。这直接引导学生学习教师的轨迹动态。具体来说，我们使用教师模型上的无分类器指导（CFG）来定义瞬时速度场：

其中 是指导尺度， 和 分别代表条件和无条件输入。通过将这个由教师定义的速度场代入MeanFlow的训练目标（方程(6)），我们构建了我们的蒸馏损失。这个阶段的产物是一个被赋予了教师结构先验的学生生成器。尽管其在最少步数下的保真度不完美，但它为后续的分布匹配和优化提供了一个适定（well-posed）的初始化。

第二阶段：分布优化

在通过第一阶段模型 初始化后，生成器 接着进入第二阶段的分布优化，恢复那些在仅从教师轨迹学习时固有丢失的高频细节。我们采用基于DMD的策略来将 的单步输出分布与真实数据分布对齐。由于 的初始分布已经占据了数据流形上的一个有利区域，与真实分布有显著重叠，DMD的训练过程更加稳定和高效。其主要任务从“盲目探索”转变为“有针对性地优化细节”。对于DMD中的分数网络，尽管MeanFlow学生模型本身可以预测瞬时速度，我们仍然使用预训练的教师模型 来初始化真实和伪造分数分支。这可以防止潜在的误差累积，并提供更准确的速度场估计。损失函数如方程(8)所示。

为了进一步稳定训练并减轻模式崩溃的风险，引入了对抗性训练策略。我们引入一个判别器D，它不在高维像素空间中进行判别，而是在教师模型 的特征空间中操作，这遵循了[29]的做法。总的对抗性损失由生成器和判别器损失 , 组成：

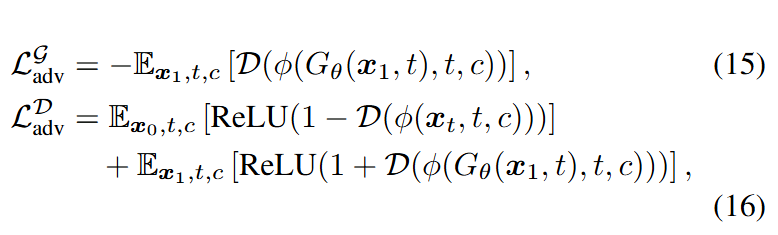
其中 表示特征提取函数，它接收图像、时间和条件作为输入，并返回教师模型 的中间特征。这里， 是一个带噪声的真实图像，而 是一个生成的样本。

最终，总损失公式为：

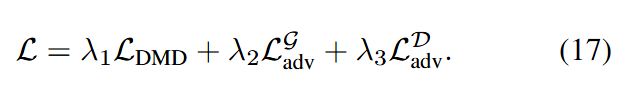
自适应加权判别器. 经过TD初始化后，学生模型已经捕捉到了目标分布的整体结构。不完美之处不再是全局性的，而是表现为微妙的、局部化的伪影。这使得依赖全局平均池化（GAP）的传统判别器在很大程度上失效。为了应对这一挑战，我们设计了自适应加权判别器（AWD），如图2底部所示。我们的判别器不是为所有令牌（token）分配统一的权重，而是采用一个可学习的查询嵌入和一个注意力机制来动态地加权特征图上的不同令牌。因此，判别器可以专注于最可能包含伪影的局部区域，为生成器提供更精确和有效的梯度。

通过这个分层框架训练出的最终学生模型，能够在最少步数下生成与多步教师模型质量相媲美的图像，同时保持多样性。

实验

实验部分首先通过一个二维玩具实验验证了其核心理论假设：轨迹蒸馏（TD）存在信息瓶颈，其性能上限受限于学生模型的能力。实验表明，增加模型容量能显著提升单步学生模型的性能，但即使容量增加50倍以上，也无法完美复制多步教师模型的轨迹，证明了仅靠TD不足以实现最优的单步生成质量，必须有后续的优化阶段。

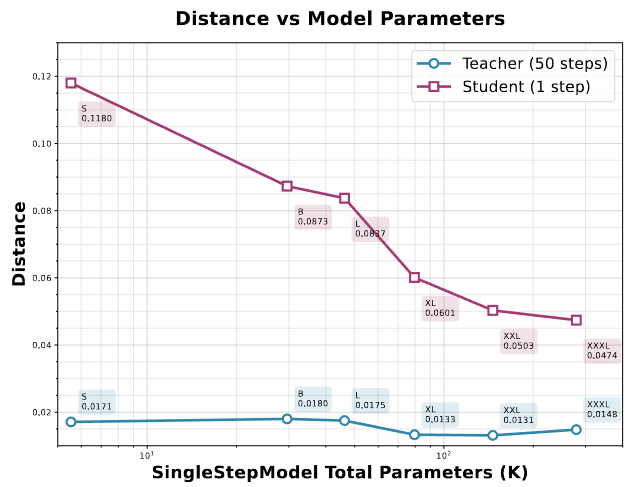
图 3.轨迹蒸馏 (TD) 性能与模型大小的关系。TD 性能的上限随着模型参数数量的增加而增加。

图 3.轨迹蒸馏 (TD) 性能与模型大小的关系。TD 性能的上限随着模型参数数量的增加而增加。

在主要对比实验中，本文在ImageNet 256×256和文生图（MJHQ-30K）两个基准上验证了HD框架的有效性。

• 在ImageNet上，HD单步模型的FID达到了2.26，优于所有其他单步方法（如MeanFlow的3.43，DMD的6.63），并且几乎与250步的教师模型（FID 2.27）持平，实现了巨大的推理加速（约70倍）而几乎没有性能损失。
• 在文生图任务上，HD在单步和两步设置下的FID和CLIP分数均优于包括SDXL-LCM、DMD2和MeanFlow在内的现有方法，证明了其方法的普适性和卓越性能。

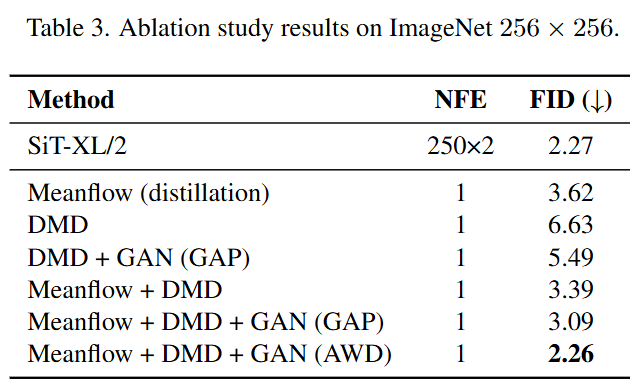
消融实验进一步剖析了HD框架各个组件的贡献。结果表明：

1. TD初始化至关重要：与没有TD初始化的模型相比，经过TD初始化的模型性能有显著提升（FID从5.49提升到3.09），证实了提供一个高质量的结构先验是成功的关键。
2. AWD的有效性：与使用标准全局平均池化（GAP）的判别器相比，本文提出的自适应加权判别器（AWD）将FID从3.09进一步降低到2.26，证明了AWD在聚焦局部瑕疵、指导模型优化细节方面的优越性。

结论

本工作为轨迹蒸馏（TD）提出了一个统一的理论公式，识别出一个共同的“平均速度”建模目标，该目标导致了一个信息论瓶颈。这一分析揭示了为何TD擅长于全局结构，却在根本上难以处理精细细节。受此启发，提出了一个新颖的分层蒸馏（HD）框架，该框架协同地结合了TD和分布匹配。本文方法首先利用TD作为一个强大的初始化器，从教师模型中注入丰富的结构先验，为学生模型建立一个适定（well-posed）的起点。随后，通过分布匹配来优化这个强大的初始模型。为了增强这一阶段，引入了一个量身定制的对抗性训练过程，并配备了本文提出的自适应加权判别器（AWD）。通过动态地关注良好初始化模型的局部伪影，它为细节优化提供了更精确的指导。大量的实验表明，本文的单步学生模型显著优于现有的蒸馏方法，并实现了与其多步教师模型相当的保真度。通过诊断并克服TD的瓶颈，本工作为少步乃至单步高保真度生成提供了一个有效的新范式。

参考文献

[1] From Structure to Detail: Hierarchical Distillation for Efficient Diffusion Model