扩散模型原理与实践:一个统一的微分方程框架
原创扩散模型原理与实践:一个统一的微分方程框架
原创
走向未来
发布于 2026-01-06 09:24:53
发布于 2026-01-06 09:24:53
扩散模型原理及其对生成式人工智能的影响
走向未来
生成式人工智能领域在过去几年经历了爆发式增长,多种模型架构涌现,各自展示了强大的能力。从生成对抗网络(GAN)到变分自编码器(VAE)再到自回归模型,这个领域似乎充满了多样化甚至相互竞争的思想。然而,扩散模型(Diffusion Models)的崛起不仅带来了一种新的、性能卓越的生成范式,更重要的是,它揭示了一个深刻的趋同现象:许多看似不同的生成方法,实际上只是观测同一个基础数学原理的不同视角。
最新的470页的电子书《The Principles of Diffusion Models —— From Origins to Advances》系统性地阐述了扩散模型的原理。该书已收录至“走向未来”知识星球中。本文基于书的核心内容,探讨扩散模型理论收敛如何为生成式人工智能提供了一个更稳定、可控和高效的未来框架,并分析其对技术产品、市场和硬件架构的深远影响。

097.jpg
第一部分:殊途同归——三种生成范正式的起源与收敛
该文件详尽地追溯了扩散模型的三个主要思想起源。这三种视角在历史上各自独立发展,分别解决了生成模型在不同方面的挑战,但最终都指向了一个共同的数学结构。

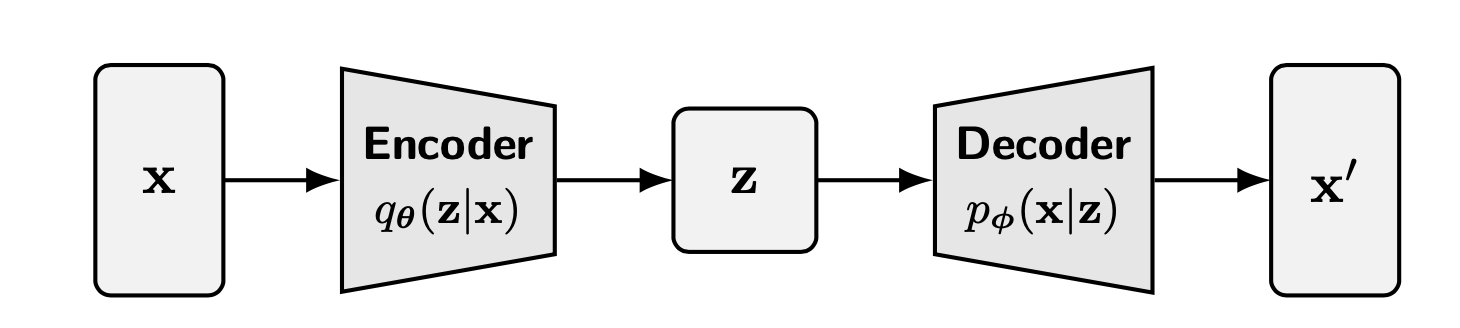
首先是变分视角。这一路径始于变分自编码器(VAE)。VAE的核心思想是学习一个从数据到低维潜在空间的编码过程,以及一个从潜在空间解码回数据的生成过程。扩散概率模型(DDPM)可以被视为这种思想的一种精妙演进。它将编码过程固定为一个逐步添加噪声的、简单的马尔可夫链。这个前向过程(编码)是固定的、无需学习的。整个模型的学习任务被简化为学习这个过程的逆向过程,即一个逐步去噪的解码器。生成过程不再是一步到位的解码,而是从纯噪声开始,通过一系列精细的、逐步的降噪步骤,逐渐恢复出结构清晰的数据。这种化繁为简的策略,将一个复杂的高维分布学习问题分解为一系列易于处理的局部去噪任务。
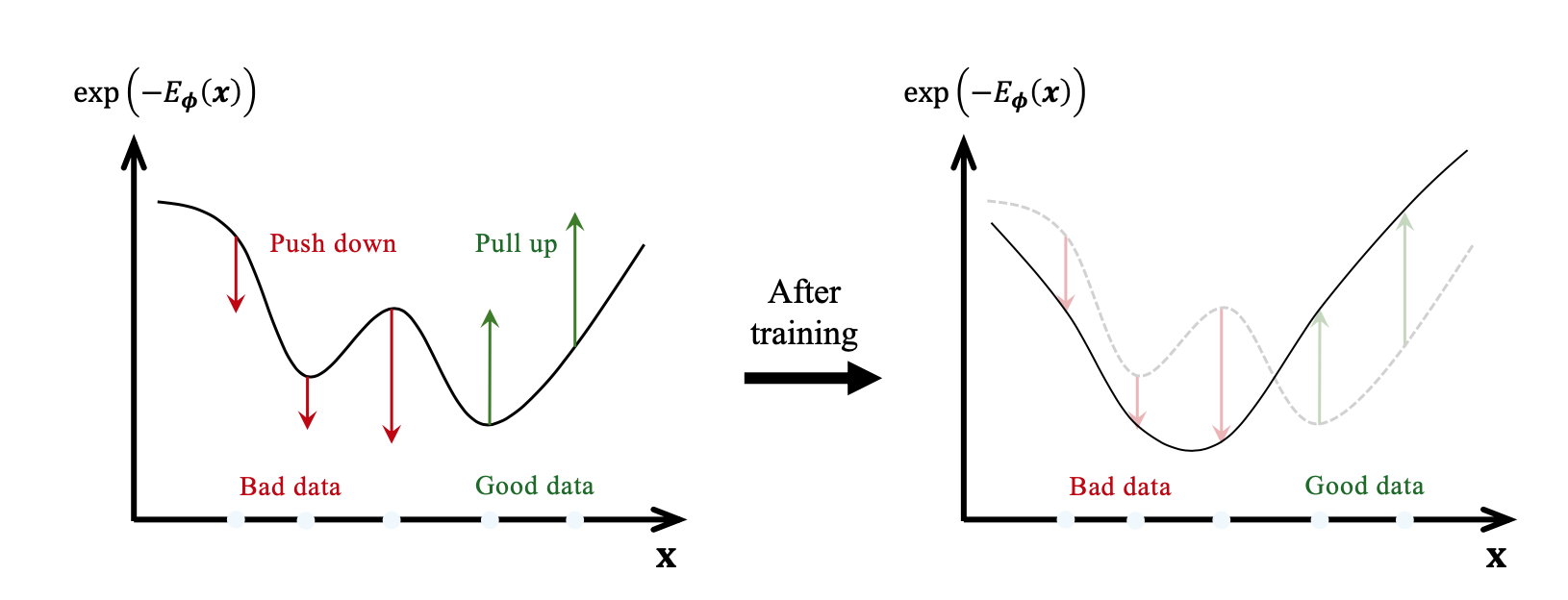
其次是基于分数的视角。这一路径源于能量基础模型(EBM)。EBM通过一个能量函数来定义数据分布,数据点对应低能量区域,而非数据点对应高能量区域。其挑战在于难以计算归一化常数。基于分数的模型(Score-Based Models)绕开了这个问题,它们选择不直接学习分布,而是学习分布的对数梯(即“分数函数”)。这个分数函数指向数据概率密度增长最快的方向。生成过程就像在一个高维山谷中放置一个球(噪声),这个球会沿着分数函数(山谷的坡度)“滚落”,最终停在能量最低的谷底,也就是高概率的数据点所在区域。该文件进一步将这个离散的步骤推广到连续时间,形成了分数随机微分方程(Score SDE)的框架。
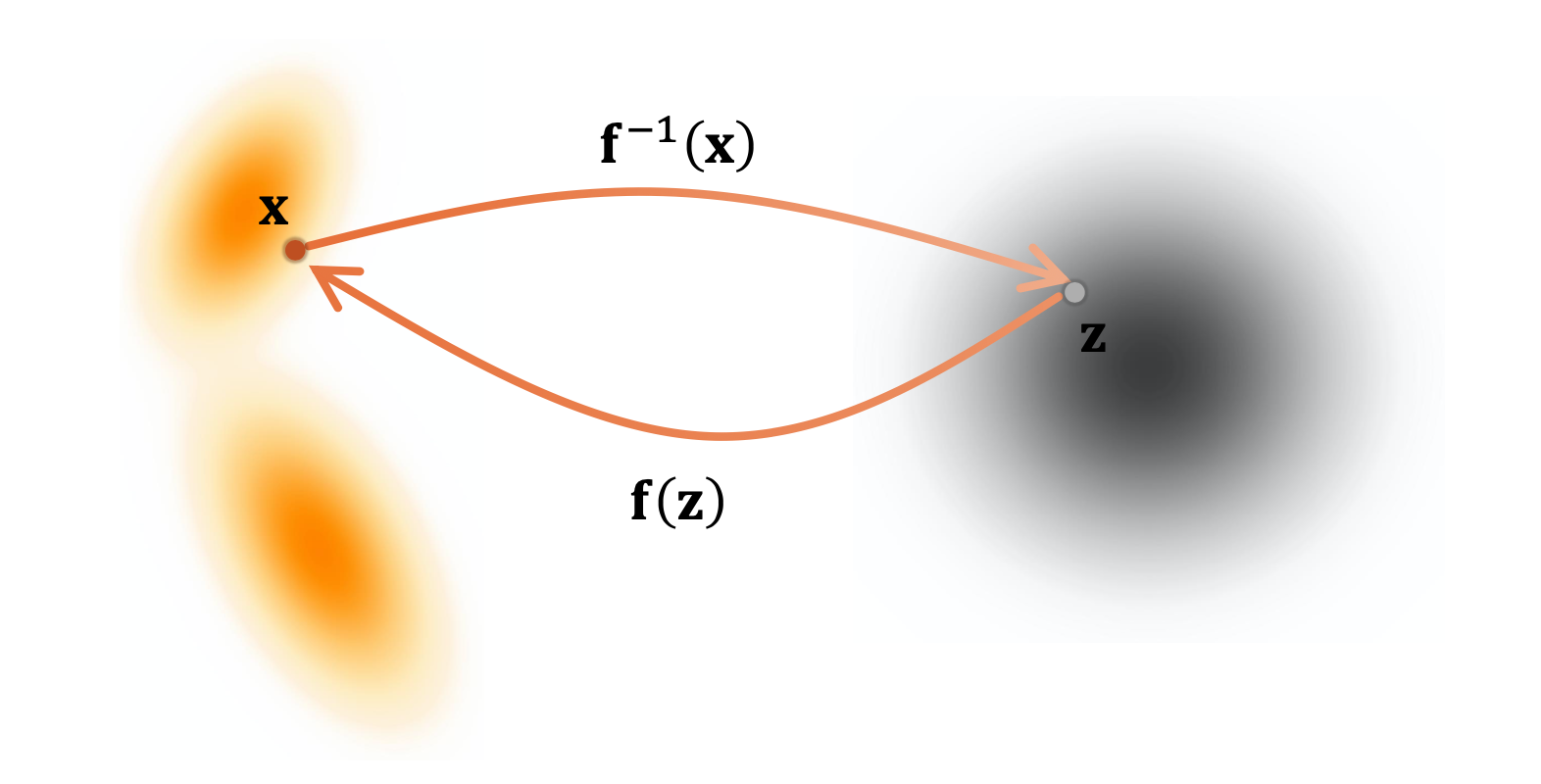
最后是基于流的视角。这一路径来自归一化流模型(Normalizing Flows)。归一化流模型学习一个精确可逆的、从简单先验分布(如高斯分布)到复杂数据分布的映射。它像一个连续的流体,将初始的简单形状“扭曲”和“变形”为数据的复杂形状。流匹配(Flow Matching)等近期进展将这一思想推广为学习一个随时间变化的“速度场”(Velocity Field)。生成过程就是从先验分布中采样一个点,然后让这个点跟随这个速度场在连续时间中“流动”,其轨迹的终点就是生成的数据。
这份文件的深刻洞察在于,它明确指出这三条路径并非相互独立,而是殊途同归。无论是VAE的逐步降噪、EBM的梯度跟随,还是NF的速度场流动,它们在连续时间的极限下,都统一指向了同一个核心对象:一个描述从噪声到数据转化的连续时间生成过程。
第二部分:生成式AI的新“物理学”——微分方程的统一框架
该文件最有价值的贡献,是它揭示了支撑上述三种视角的共同数学基础。这个基础就是微分方程的语言。这种统一不仅是理论上的优雅,更是实践上的巨大飞跃。

生成过程被重新定义为求解一个微分方程。在这个统一框架中,无论是随机微分方程(SDE)还是常微分方程(ODE),都描述了一个连续的轨迹,这个轨迹的一端是来自先验分布的纯噪声,另一端是目标数据。模型的神经网络(无论它被称为去噪网络、分数网络还是速度场网络)所学习的,正是这个微分方程的“力场”或“速度场”。这个场在每个时间和空间点上,都为噪声点提供了下一步该如何“演化”的精确指导。
这种统一的核心原理是概率流。随机微分方程(SDE)描述了单个粒子(样本点)在力和随机扰动(噪声)共同作用下的随机轨迹。而与之对应的福克-普朗克方程(Fokker-Planck Equation),一个偏微分方程(PDE),则描述了整个粒子“云”(即概率分布)的密度如何随时间演变。常微分方程(ODE)则提供了这个过程的确定性版本,它描述了概率“质量”本身是如何确定性地流动的。

4.jpg
文件指出,三种视角都巧妙地利用了“条件化技巧”(Conditioning Trick)来解决训练中的核心难题。直接匹配模型分布与真实数据分布(一个未知的、极其复杂的目标)是极其困难的。相反,所有这些方法都将问题转化为匹配一个已知的、易于计算的条件分布。例如,DDPM学习的是在给定原始数据x0的情况下,从xt去噪到xt-1的条件概率;分数模型学习的是在给定x0的情况下,噪声数据xt的分数;流匹配则学习在给定x0和x1(噪声)的情况下,两者之间的流动速度。通过这种方式,一个无法解决的全局匹配问题被转化为一个可以被有效监督和学习的局部预测问题。
将生成式建模建立在微分方程的坚实基础之上,意味着我们为生成式AI找到了一套“物理学”。我们不再是仅仅依靠经验和直觉拼凑神经网络架构,而是可以利用数学和物理学中经过百年验证的工具来分析、控制和优化生成过程。这为整个领域带来了前所未有的稳定性和可预测性。
第三部分:统一框架的实践红利——可控、高效的产品化平台
将生成式AI重新表述为“求解微分方程”,绝非纯粹的理论游戏。正如文件后续章节所展示的,这种新视角直接催生了巨大的实践红利,彻底改变了生成式AI产品的形态和能力边界。
首先,它彻底重构了“采样”问题。在传统的GAN或VAE中,采样是一次性的前向计算。在扩散模型中,采样等同于数值求解一个ODE或SDE。这在初期被视为一个巨大缺陷,因为它需要数百甚至数千次迭代计算,导致生成速度极慢。但这种新框架的优势在于,它将“加速采样”问题转化为了一个在应用数学中已被深入研究了几十年的问题:“高效ODE求解器”。
这立刻打开了一个全新的创新空间。DDIM的提出,展示了可以通过一个非马尔可夫过程来跳跃式采样。随后的DPM-Solver、DEIS等一系列工作,更是将数值积分的先进技术(如指数积分器、高阶方法)引入生成模型。其结果是革命性的:原本需要数千步的采样过程被压缩到10至20步,在几乎不损失质量的前提下,将生成速度提升了百倍。这使得扩散模型在产品化应用中的延迟瓶颈得到了根本性的缓解。
著名的“无分类器指导”(Classifier-Free Guidance, CFG)就是这一思想的直接产物。在每一步积分时,模型计算两个速度:一个无条件的(模型自己想画的)和一个有条件的(例如,根据文本提示“一只猫”)。最终的速度场被设为这两者的加权外推。这种在采样过程中动态“引导”轨迹的能力,使得扩散模型获得了惊人的可控性。更重要的是,这个控制模块是“即插-即用”的。我们可以训练一个通用的、无条件的“生成引擎”(基础速度场),然后在推理时,根据不同任务(如图像编辑、风格迁移、文本生成图像),加载不同的“引导模块”(附加的速度场)。这种模块化的产品架构极大地提升了模型的复用性和灵活性。
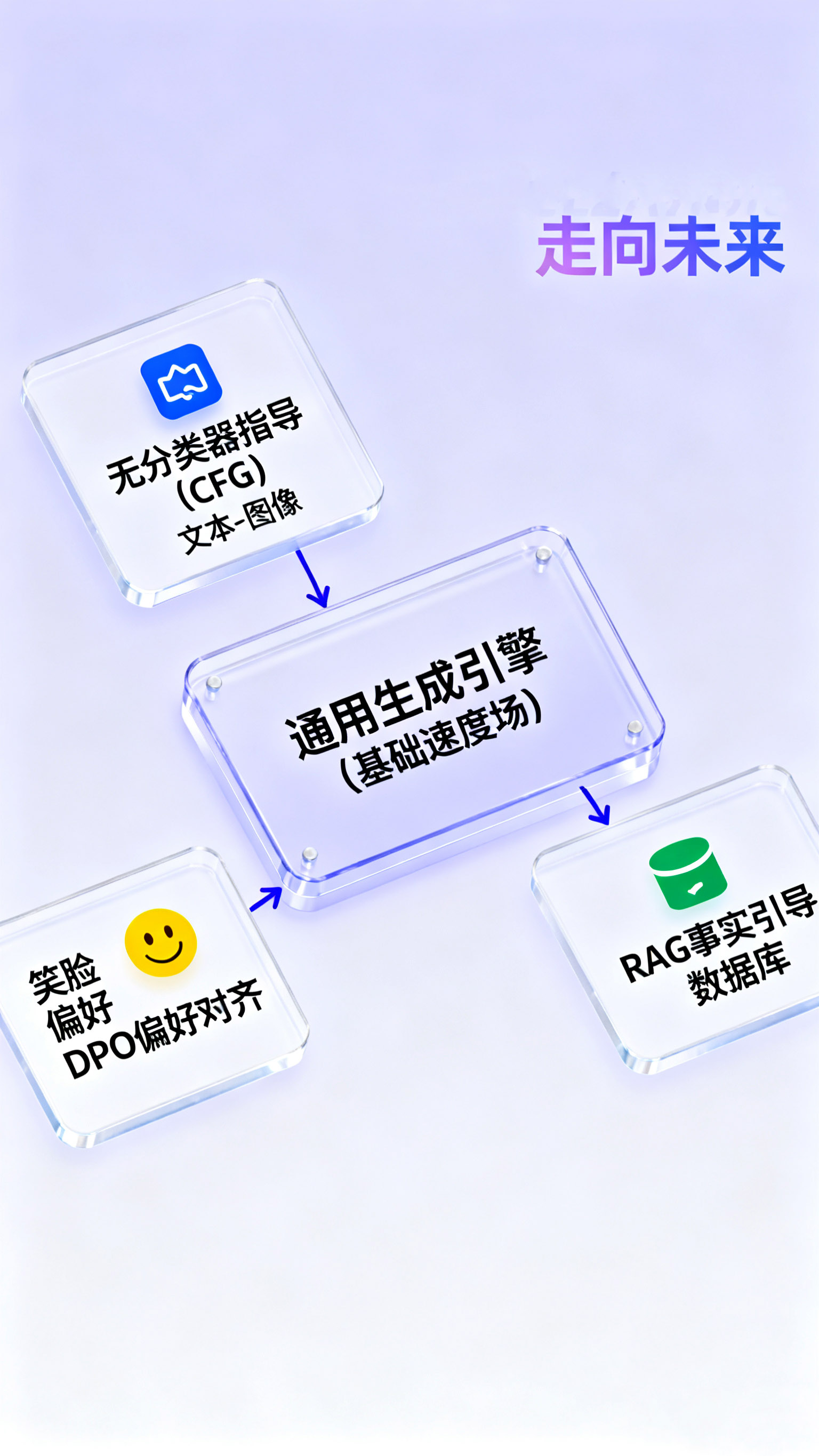
3.jpg
这种控制甚至可以扩展到人类偏好。我们可以将人类的偏好(例如,一张图片是否“美观”或“安全”)建模为一个奖励函数,并将其梯度也作为一个引导向量添加到ODE求解中。这就引出了DPO(直接偏好优化)等对齐技术在扩散模型中的应用,使得模型可以根据复杂的人类反馈进行微调。
这种对生成轨迹的“引导”,不仅解决了风格与偏好的对齐问题,也为攻克生成式AI的另一核心顽疾——即大语言模型中常见的“幻觉”(Hallucination)与知识陈旧——提供了清晰的路径。AI芯片与大模型技术专家王文广,在其深入探讨AI范式演进的灯塔书《知识增强大模型》中,便系统性地阐述了这一方向。该书明确指出,无论是基于Transformer的语言模型还是基于扩散的生成模型,其强大的涌现能力必须与外部的、可验证的知识体系相结合,才能构建真正鲁棒和可信的AI应用。
王文广在书中重点论述的“检索增强生成”(RAG)与“图模互补”(Graph-Model Complementation)两大范式,其核心原理与扩散模型的“引导”机制可谓异曲同工。如果说CFG和DPO是在ODE求解的每一步动态修正“速度场”以对齐“风格”或“偏好”;那么RAG和GraphRAG就是在利用外部知识库(如向量数据库或知识图谱)对生成的内容进行“事实引导”。这进一步印证了本文的核心观点:一个统一的、模块化的“生成引擎”(无论是基于扩散的ODE还是基于Transformer的LLM)与一系列可插拔的“引导模块”(无论是偏好、风格还是外部知识)相结合,构成了现代生成式AI产品化的坚实基础。
第四部分:下一轮演进——从“学习过程”到“学习解”
微分方程框架虽然强大,但求解过程始终是迭代的。一个自然而然的终极问题随之而来:我们能否绕过求解过程,直接学习这个微分方程的“解”?
这个“解”在数学上被称为“流图”(Flow Map)。流图Psi(x_s, s, t)是一个函数,它可以一步到位地将一个在时间s的状态x_s直接映射到时间t的状态x_t。如果我们能学到这个函数,特别是Psi(x_T, T, 0)(从纯噪声到数据),我们就实现了单步(One-Shot)生成。这兼具了GAN的速度和扩散模型的质量与可控性。

1.jpg
文件所探讨的最新进展,如“蒸馏”(Distillation)和“一致性模型”(Consistency Models),正是朝着这个目标迈进。
蒸馏(Distillation)是第一种尝试。它采用“教师-学生”模式。我们首先拥有一个缓慢但高质量的“教师”模型(一个完整的扩散ODE求解器)。然后,我们训练一个“学生”网络,这个学生网络的任务就是模仿教师的“两步”结果。例如,学生学习一步从t_k跳到t_{k+2},使其结果与教师模型从t_k到t_{k+1}再到t_{k+2}的两步结果相同。通过“渐进式蒸馏”(Progressive Distillation),学生模型可以迭代地将教师模型的步数减半,最终实现仅用几步甚至一步就完成高质量生成。
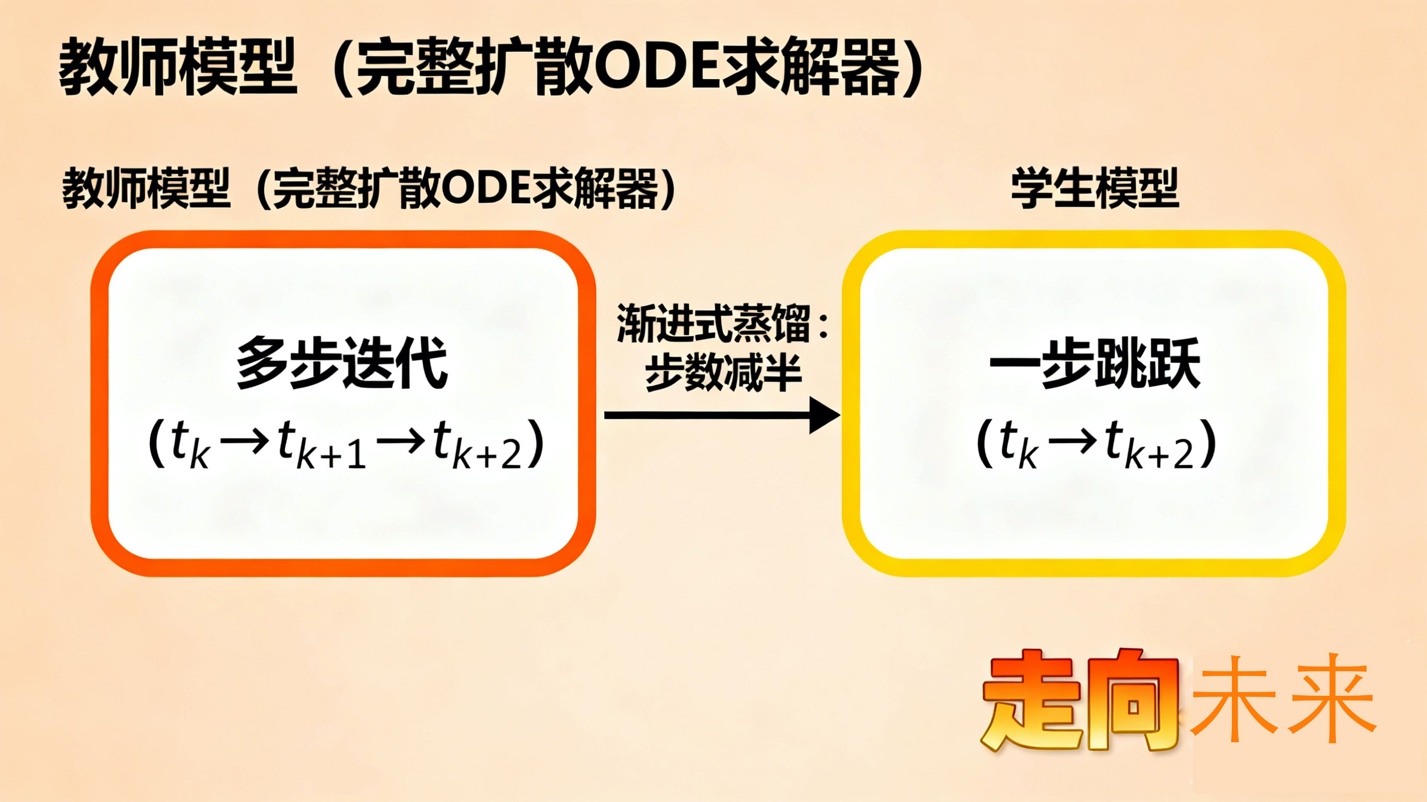
2.jpg
而“一致性模型”(Consistency Models, CM)则更加彻底。它们试图“从零开始”(from scratch)直接学习流图,而无需依赖预先训练好的教师模型。一致性模型的核心思想源于ODE流图的一个基本数学性质:沿着任何一条ODE轨迹,所有点最终都会流向同一个终点(即x_0)。因此,模型被训练来使其输出在一条轨迹上的任意两个点(例如x_s和x_t)上都保持“一致”,即f(x_s, s)应该等于f(x_t, t)。通过强制模型在整个时间和空间上满足这种一致性,模型最终学会了f(x, t) = x_0,即直接预测轨迹的终点。一致性轨迹模型(CTM)进一步将其推广到学习任意时间点s到t的流图,实现了更灵活的生成控制。
这一系列从“学习速度场”到“学习流图”的演进,代表了生成模型在原理上的又一次飞跃。它不再学习一个需要迭代求解的过程,而是直接学习这个过程的最终解。
结论:统一框架的市场与技术价值
这份技术文件所勾勒的,不仅仅是扩散模型的数学原理,更是一个正在发生的、影响深远的范式转移。从产品、技术和市场的角度来看,这种从分歧走向统一的趋势具有重大价值。
在技术和产品层面,“微分方程框架”提供了一个前所未有的稳定和模块化的平台。未来的生成式AI产品将不再是孤立的、端到端的黑盒。它们将演变为一个“基础引擎”(学习通用的速度场或流图)和一系列可插拔的“应用模块”(如ODE求解器、控制引导器、对齐模块)的组合。企业可以专注于训练一个强大的基础引擎,而社区和第三方开发者则可以围绕这个引擎开发各种高效的求解器和新奇的控制功能。这极大地降低了创新的门槛,加速了生态的繁荣。
在硬件和市场层面,这种转变正在重塑AI芯片的竞争格局。GAN和VAE的单步前向传播对推理硬件的需求相对简单。而扩散模型的迭代特性,则对芯片的片上内存(SRAM)和内存带宽提出了极高的要求,因为每一步的中间状态都需要被快速读写。然而,“学习流图”的新趋势(如一致性模型)又将竞争带回了单步推理的战场,但要求单次计算的精度和复杂度远超以往。这种算法上的快速演进,迫使AI芯片市场必须保持极高的灵活性,以适应从“迭代求解”到“单步映射”的快速切换。这一系列深刻的技术变革与市场趋势,正是需要行业同仁共同深入探讨的议题。欢迎加入最具价值的知识星球“走向未来”,一起探讨生成式人工智能、大模型、AIGC、AI芯片和机器人等的产品、技术和应用实践,探讨如何使用各种不同的人工智能大模型和智能体来为工作增效,为生活添彩。立即加入“走向未来”知识星球,一起走向AGI的未来。

016.jpg
总之,扩散模型的原理统一,标志着生成式AI正在从一个“炼金术”般的、依赖经验技巧的领域,转变为一个基于“物理学”(即微分方程)的、有章可循的工程学科。这为实现更鲁棒、可控、高效的通用人工智能奠定了坚实的理论基石。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
评论
登录后参与评论
推荐阅读
目录

