双运放带通滤波器 (Dual Amplifier Band-Pass Filter, DABP)

不记得是哪个文章，有个读者说了一个滤波器，我只有搜索到了一个ADI的文档：

很短

很短

想起来了，是LMC6482的文章来着；滤波器其实有不少，但是也不多，其实就是滤波器的参数很多，没有一个是完美的，所以先聊聊这个滤波器的适用情况；其实主要是 “窄带滤波（Narrow-Band Filtering）” 。

窄带滤波器：带宽 远小于中心频率 ，即 。

常见判定：若 ，一般可视作“窄带”。

例如：，则 ，属于典型窄带。

只允许极窄的频段通过，抑制掉上下频率成分；可用来“锁定”目标频率（如谐振点）。另外窄带意味着 元件误差/温漂/运放特性 对性能影响更大；稍有偏差，中心频率就可能漂移。但是窄带滤波常伴随较大的 群延迟，会使时域信号拉长、相位旋转更敏感。不过窄带信号的噪声与干扰抑制能力强能把宽带噪声“削掉”，仅保留极小的频率窗口。

实现方式：有源模拟滤波

MFB (多重反馈)：结构简单，但高 Q 时灵敏度高、运放要求严苛。

DABP (双运放带通)：适合高 Q，参数解耦，稳定性好。

注意点

运放 GBW 要足够高，高 Q → 带通峰值增益可能放大几十倍 → 运放必须有足够余量；窄带设计对 R/C 偏差极敏感，需用 1% 甚至 0.1% 精度电阻、电容；另外窄带会提高噪声功率密度的影响（信号能量集中，噪声底抬升）。

双运放带通滤波器 (Dual Amplifier Band-Pass Filter, DABP)

高 Q、高频应用

传统带通滤波器在高 Q 值（窄带）时，元件容差和放大器特性敏感度很高；DABP 结构具有低灵敏度和低元件分布差异（element spread 小）；其中谐振频率 主要由 R2 控制；Q 值主要由 R1 控制，这样可以相对独立地调节性能参数。

最好是使用双运放实现，因为使用一颗双运放芯片中的两个匹配放大器，匹配性能降低了 Q 值对放大器参数（增益带宽、失调、噪声等）的敏感度。

DABP 的一大优势是 对元件公差和运放特性的敏感度较低：电容与电阻的匹配性要求比 MFB 低；因为采用了对称结构（R2 = R3, R4 = R5），容差对谐振点的漂移影响较小；对运放 GBW 和相位裕度要求降低，因此在高频应用中更稳定。

电路结构（Figure 1）

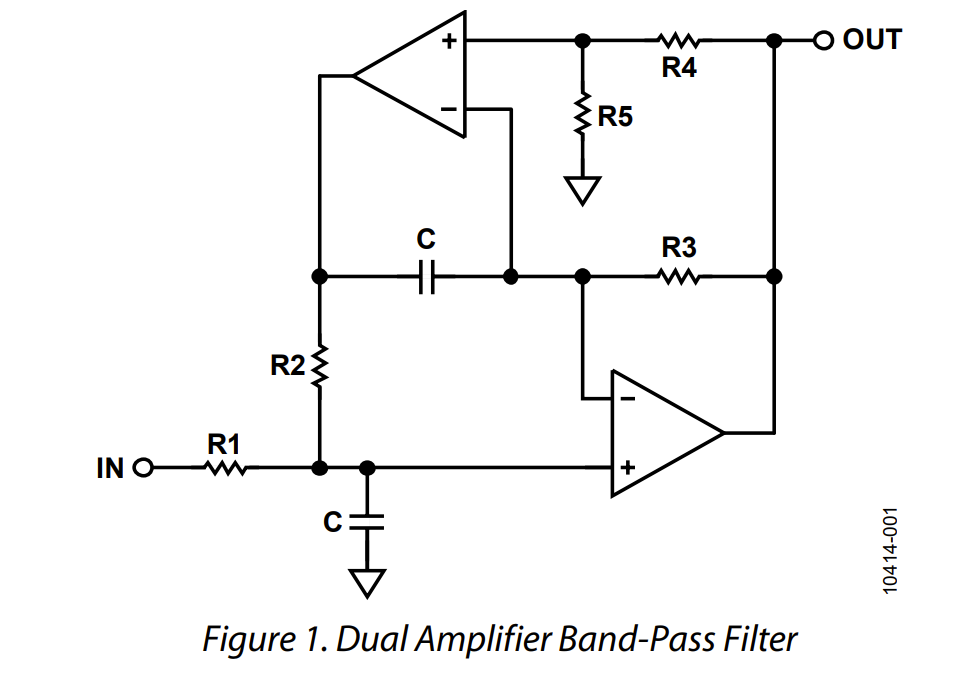
这样的

这样的

输入电阻 R1，反馈网络由 C、R2、R3、R4、R5 构成；输出在谐振点处有一个固定增益 2 倍。

增益控制

如果需要 小于 2 倍增益：可以将 R1 分为 R1A 与 R1B，形成分压器；文档给出了增益小于 2 的公式修正。

传递函数与设计方程（Figure 2，原文）

传递函数形式为：

其中：

—— 谐振角频率

Q 值与电阻比相关，可独立调节

设计步骤：

1. 选择 C 和 R4（电容与一个电阻作为起点）。
2. 令 R5 = R4。
3. 确定谐振频率：
4. 设置 Q 值：
5. 其余电阻根据关系式设置：，

在需要高选择性（窄带滤波）的场合，如 通信接收机前端、谐振检测、传感信号调理，DABP 优势明显；相比单运放多反馈带通滤波器（MFB-BPF），DABP 在高 Q 时稳定性更好；缺点是运放数量增加，电路复杂度稍高。

Q 值与带宽

Q 值与带宽关系：

在 DABP 中：

R1 控制 Q 值。

Q 值越高，带宽越窄，频率选择性越好。

高 Q 时，传统滤波器对运放增益带宽积 (GBW) 要求极高，但 DABP 结构因为双运放分担了环节，稳定性更强。

与其它带通滤波器对比

实际设计

假设要设计一个 中心频率 10 kHz，Q=10 的带通滤波器：

选电容 。

计算谐振电阻：

→ 取 。

设定 Q 值：通过调节 R1 选择合适阻值；R4, R5 选择一个方便的标准值（如 10 kΩ），并保持相等；使用双运放芯片（如 AD8672，GBW=10 MHz）即可满足需求。

做一个 Python 仿真 ，绘制 DABP 滤波器在不同 Q 值下的幅频响应：

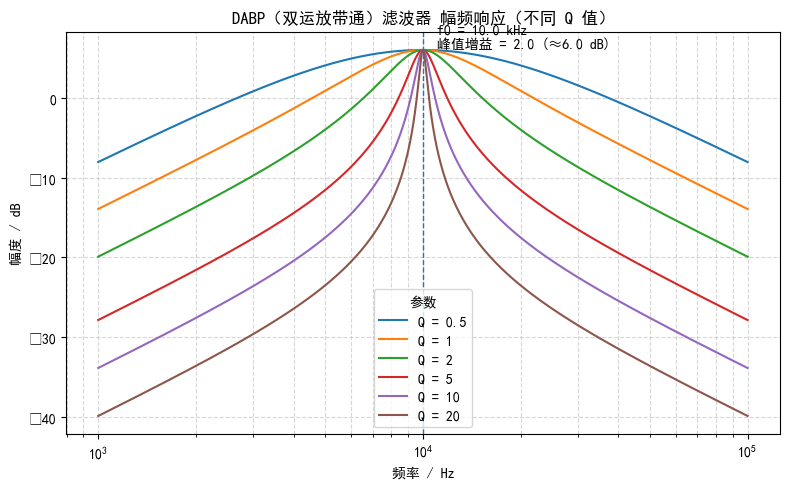
Bode 图

Bode 图

采用传函 ，令峰值增益 （与 MT-209 描述一致），在 处幅度 ≈ 6.02 dB。

提高 会明显变窄带宽、增强选择性；低 则带宽更宽、峰值更钝；频率轴覆盖 到 ，默认 kHz，可在代码顶部改参数。

# DABP（双运放带通）滤波器幅频响应仿真
# 说明：
# 1) 采用经典二阶带通传函：H(s) = k * (ω0/Q) * s / (s^2 + (ω0/Q) * s + ω0^2)
# 2) 在 ω = ω0 处的峰值增益为 k。根据 MT-209 描述，取 k = 2（谐振点处增益为 2）。
# 3) 扫描不同 Q 值，绘制幅频响应（dB），直观比较带宽与选择性。
#
# 使用方法：直接运行即可看到一张幅频响应图。
#
# 备注：
# - 不使用 seaborn；只用 matplotlib。
# - 每张图只含一个绘图区域（无子图）。
# - 未指定任何配色方案。

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'SimHei'  # 替换为你选择的字体
# --------- 参数区 ---------
f0 = 10e3     # 中心频率（Hz），可根据需要修改
k  = 2.0      # 峰值增益（在 f0 处），依据 MT-209 默认 2 倍
Q_list = [0.5, 1, 2, 5, 10, 20]  # 不同的 Q 值用于比较

# 频率轴：采用对数刻度覆盖 0.1*f0 到 10*f0
f = np.logspace(np.log10(f0*0.1), np.log10(f0*10), 2000)
w = 2*np.pi*f
w0 = 2*np.pi*f0

# 计算幅频响应
def H_bp(jw, w0, Q, k):
    # H(jw) = k * (w0/Q) * (j*w) / ( (j*w)^2 + (w0/Q)*(j*w) + w0^2 )
    s = 1j * jw
    num = k * (w0/Q) * s
    den = s**2 + (w0/Q)*s + w0**2
    return num / den

plt.figure(figsize=(8, 5))
for Q in Q_list:
    Hjw = H_bp(w, w0, Q, k)
    mag_db = 20*np.log10(np.abs(Hjw) + 1e-20)  # 避免log(0)
    plt.semilogx(f, mag_db, label=f"Q = {Q}")

# 图形标注
plt.title("DABP（双运放带通）滤波器 幅频响应（不同 Q 值）")
plt.xlabel("频率 / Hz")
plt.ylabel("幅度 / dB")
plt.grid(True, which="both", ls="--", alpha=0.5)
plt.legend(title="参数", loc="best")

# 在图上标出中心频率 f0 与峰值增益 k
peak_db = 20*np.log10(k)
plt.axvline(f0, linestyle="--", linewidth=1)
plt.text(f0, peak_db, f"  f0 = {f0/1e3:.1f} kHz\n  峰值增益 = {k:.1f} (≈{peak_db:.1f} dB)",
         va="bottom", ha="left")

plt.tight_layout()
plt.show()