ADC 的缓冲带宽如何微调？（YUNSWJ 仿真版）

ADC 的缓冲带宽如何计算？（YUNSWJ 仿真版）

昨天写了关于缓冲器带宽的文章：

后面还有一段这个

后面还有一段这个

文中以 20 位 ADC 举例：估值因子 ≈ ，使得缓冲频率 ≈ 奈奎斯特频率的 9 倍。

什么是估值因子?

当我们要求 ADC 在采样窗口 内达到 位精度时，必须让误差指数衰减到 以下。把这个条件改写成对带宽的要求时，会出现一个系数 。这里的 就被称作**估值因子。

对于 20 位 ADC，假设预留 位容差，那么估值因子就是 或 （文档里用的是这两种近似写法）。

把它代入带宽公式

就能算出所需的最小缓冲带宽。

在文档示例中，20 位、、 时，估值因子对应的带宽大约是 75 MHz。 “估值因子”就是从 ADC 分辨率要求中提炼出来的一个数值系数，它把“需要多少位有效精度”转换成“缓冲器需要多大带宽”的量化指标。在工程上，它用来快速估算缓冲器带宽和采样窗口的关系。

关于建立的动态过程

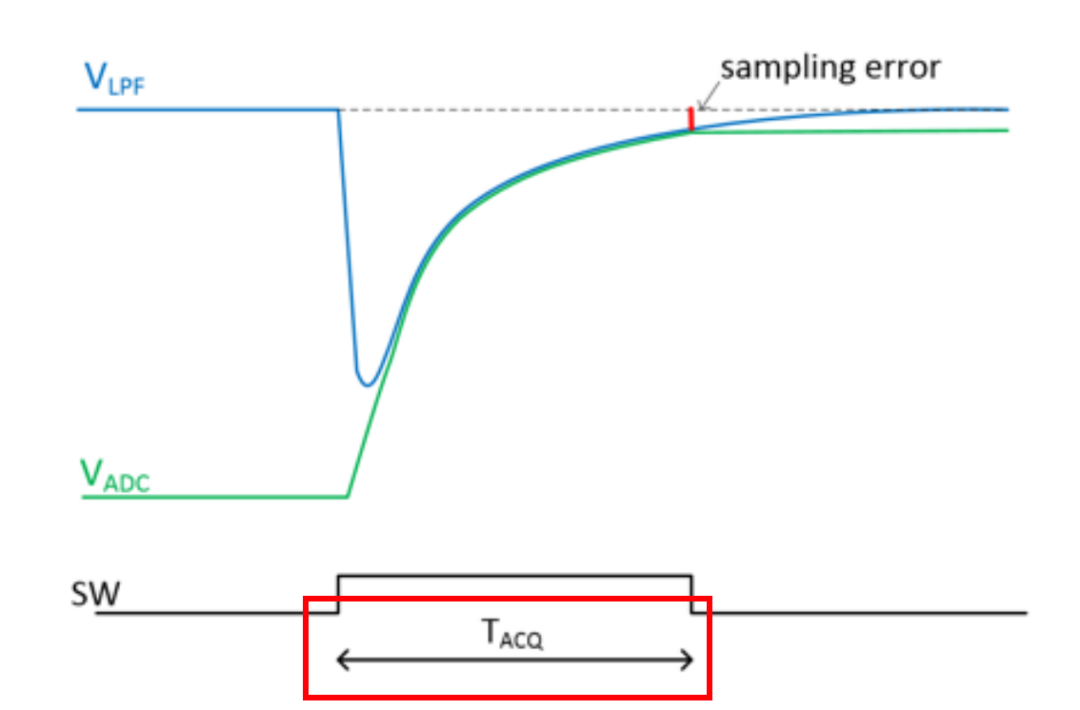
有了我们文章里面的意思

有了我们文章里面的意思

图是ADC 采样瞬间，缓冲器输出节点 与 ADC 采样电容 之间的动态过程

左边是缓冲器+低通滤波器节点电压 （蓝色）。

右边是 ADC 采样电容两端电压 （绿色）。

采样开关 SW 在采样窗 打开，ADC 输入电容开始充电。（其实是一个时序图）

详细的工作过程

开关刚闭合的一瞬间

节点电压骤然下跳（蓝色曲线陡降），这是因为 ADC 输入电容 和低通电容 发生电荷共享 → 出现 kickback 毛刺；同时，ADC 输入端电压 （绿色）从原来的保持值跃迁到新的共享电压。

采样窗内的指数恢复

接下来的 时间里，节点通过 + 的一阶 RC 电路逐渐恢复，曲线是典型的指数形态；目标是让 与 都逐渐逼近真实信号 。

采样窗结束时

SW 关闭，ADC 把当时 的电压作为量化输入；如果指数恢复来不及完全到位，就会残留一个偏差（图中标的红色短线 “sampling error”）；这个偏差正是前面公式里说的 ****。

参数表达

初始跌落幅值 = ，决定了蓝色曲线下跳的深度。

恢复速度 = ，决定了蓝色曲线回升的快慢。

最终残余误差 = ，对应图中红线。要求小于 FS，才算满足 N 位采样精度。

工程考虑（就是不需要推理，直观感受）

采样窗 越短，曲线回升不完全，sampling error 越大 → 对驱动器带宽要求更高。

增大 可以减小初始跌落，但也会拉长 ，可能来不及恢复 → “加电容 vs 带宽不足”的矛盾。

减小 能加快恢复，但会增加驱动器电流负担。（这段内容是细微调整，看下文）

增加缓冲器滤波器带宽的两种手段

假如应用需要更宽带宽（比如高速信号或高分辨率 ADC），通常有两种方法：

方法 1：增加电容

电容变大 → 反冲幅值下降 → 节点电压更平稳，缓冲器在更“线性”的条件下工作。

小电容时，另一端的噪声谱密度较低（低噪声），大电容反而能改善某些失真。

电容大 → 增加驱动器负载（交流负载 + 功耗），可能导致驱动器不稳定或过热；过大电容会限制信号带宽（因为要充电的呀！），丢失高速采样能力。

方法 2：增加电阻

电阻大 → 缓冲器驱动负载电流减小，减轻缓冲器负担，降低动态功耗，还能延长驱动器寿命。

电阻过大（比如增加 5 倍） → 失真显著增加，因为 ADC 输入的所有非线性充放电电流都要通过电阻，电压降随之放大，线性度受损。

另外也可以看出来带宽不是越大越好：满足采样建立时间即可，多余带宽只会引入额外噪声/干扰折叠。

带宽随占空比变化：采样占空比越小，所需带宽越小，可以主动降低缓冲带宽来减噪；低速 ADC 的优势是时窗更长，允许用更低带宽的缓冲器来减少噪声。（这也是和我们的直觉一样的，时间长积分更加的准确）

在文章的一开始有一段推导，有上面的铺垫就可以算了

在文章的一开始有一段推导，有上面的铺垫就可以算了

它的意思是活如果一阶滤波器占空比 40%，缓冲频率甚至会上升到 14.7 × 奈奎斯特频率；这样，缓冲器的噪声带宽会达到 ADC 噪声带宽的 15 倍。以意思就是说：缓冲器带宽过宽 → 更多高频噪声进入，再通过采样过程折叠到 Nyquist 以内，最后都落入基带噪声里；若降低采样占空比（比如从 40% 降到 20%~25%），带宽也会随之减小，折叠噪声降低；但是只要缓冲器带宽明显大于 ADC 带宽，所有噪声都会折叠回零频附近，外部干扰/杂散也会被折叠，导致噪声地板升高。

好，这段话其实是在量化缓冲器带宽相对于 ADC Nyquist 频率的放大倍数。

Nyquist 频率 = 采样频率 的一半，即 。

对于高速高分辨率 SAR ADC，要在采样窗 内满足 N 位精度，缓冲器极点频率 必须远高于 Nyquist；这个高倍关系就是通过 估值因子 推导出来的。

估值因子与倍数

前面公式：

又因为

所以带宽和 Nyquist 之比：

这就是“缓冲器带宽相对 Nyquist 的倍数”。

代入 20 bit 的情况

，假设 。

则有效位数 = 17。

倍数 = 。

为什么文中写成 ≈ ，最后说 ≈ 9 倍？ 我觉得可能是因为在实际设计里，公式会再乘一个安全裕量因子（估值因子），常近似取 ，即 。这样算下来：

那为什么会变成 14.7 倍?

如果用 一阶滤波器 + 占空比 40% 的条件，等效带宽还要乘上一个因子（因为采样有效时间更短，要求带宽更大）;文中算出来的结果就是 。

那最终的“15 倍噪声带宽”？

缓冲器的噪声带宽 ≈ 。

如果 ，那么噪声带宽 ≈ 。

而 ADC 自身的噪声带宽 ≈ ；两者相除，大约就是 15 倍。

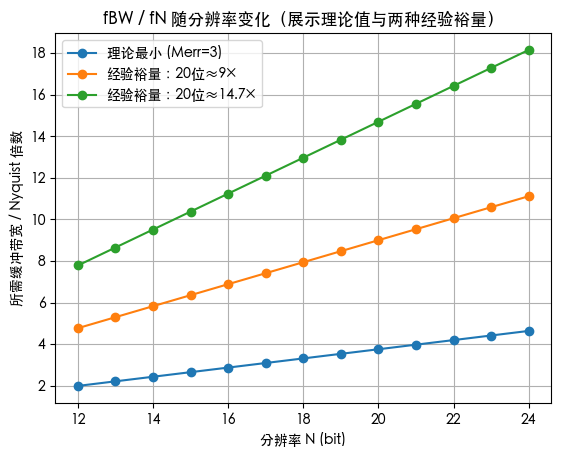
image-20250928213005453

显示 随分辨率 N 变化的三条曲线：“理论最小值”曲线（按上式、取 ）；“经验裕量：20 位≈9×”曲线（把理论曲线整体乘上常数，使在 20 位处等于 9）；“经验裕量：20 位≈14.7×”曲线（同理，使 20 位处等于 14.7）。分辨率越高，缓冲带宽必须远高于 Nyquist 的倍数也越大

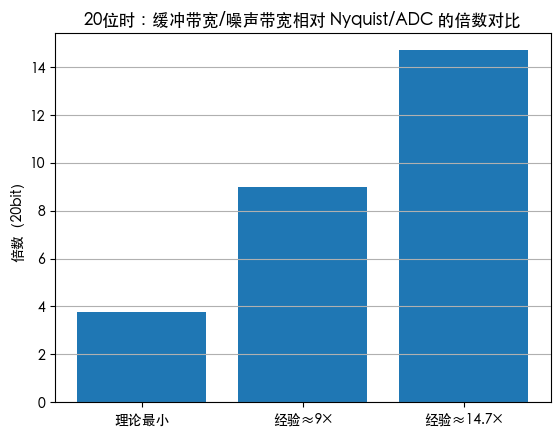
image-20250928213011414

在 20 位处，把三种倍数并排对比（也等于“缓冲噪声带宽/ADC 噪声带宽”的倍数，因为两者 NBW 都近似 乘极点频率，比例相同）。 文档指出此时缓冲噪声带宽可达 ADC 的约 15 倍，与 14.7×非常接近，工程上常用 15× 表述。

推导（已证明）：

其中 是给其他误差预留的位数。这个式子给出理论最小带宽需求与 Nyquist 的比值。文档示例（20 位、常取 ）会在此基础上再乘“工程裕量”，从而得到约 9×与约 14.7×\两种典型取值（后一种与“一阶滤波器占空比 40%”相关的更严格场景）。

这些数字出自文档原文：20 位的“估值因子”使缓冲频率约为9× Nyquist；若一阶滤波器占空比 40%，则约 14.7×；因此缓冲器的噪声带宽可达 ADC 的 15×（量级一致）。

总结一下

缓冲器带宽过宽 → 更多高频噪声进入，再通过采样过程折叠到 Nyquist 以内，最后都落入基带噪声里。

若降低采样占空比（比如从 40% 降到 20%~25%），带宽也会随之减小，折叠噪声降低；但是只要缓冲器带宽明显大于 ADC 带宽，所有噪声都会折叠回零频附近，外部干扰/杂散也会被折叠，导致噪声地板升高；所以努力减小缓冲器带宽十分重要。