从MAX6226 基准看NR降噪电容（YUNSWJ 分析版）

来自美信出品的顶级基准：MAX6226（实在不知道价格版）

前几天写了这个基准以后，其实我还有不少遗留的稿子没发，现在整理一个 NR电容的东西。

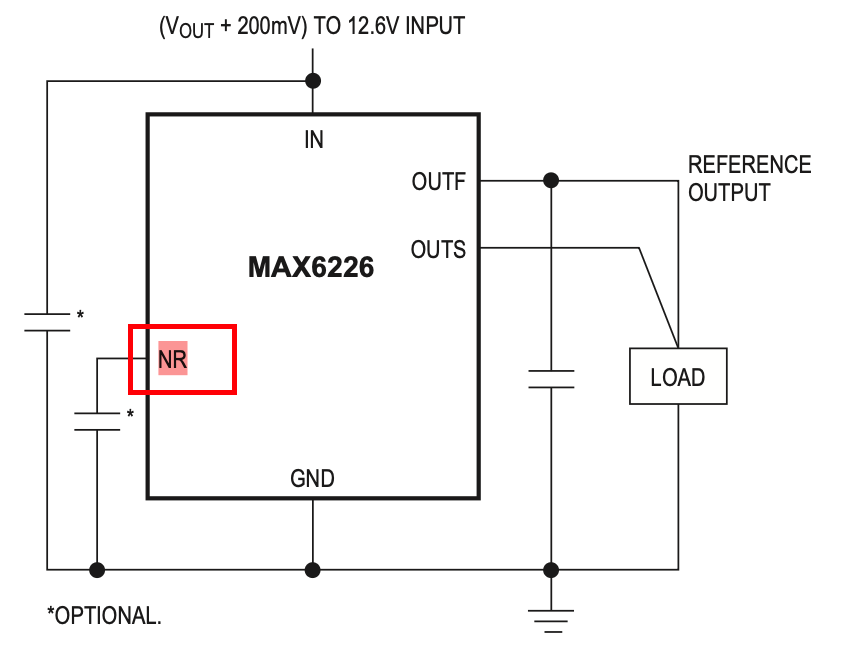
在这里

在这里

（现在我们讨论两个问题～）

1）这颗基准本身“有多干净、多稳”；（就是长期稳定性）

2）NR 电容到底在干什么。

那MAX6226 噪声和长期稳定性怎么评价？

下面以 2.5 V 版本（MAX6226_25）为例，其他电压只是成比例放大。

低频 0.1–10 Hz 噪声

数据：0.1–10 Hz 内 1.45 µV（典型）。

换成 ppm（相对 2.5 V）：1.45 µV / 2.5 V ≈ 0.58 ppm。

粗略折算成 RMS（把窗口噪声波形当成高斯统计，σ）：σµµ，约 0.09 ppm。

即便在 0.1–10 Hz 这么窄的带宽里盯着它，输出晃动也只有几 10 万分之一，是“高精密电压基准”那个级别。

宽带噪声（白噪声）

在闲鱼还看到一个白噪音发生器

在闲鱼还看到一个白噪音发生器

1 kHz 处的噪声密度：

NR 悬空：75 nV/√Hz；NR 接 0.1 µF：45 nV/√Hz。

先看一个典型 ADC 场景——假设前端带宽 10 kHz：

不接 NR：µ

接 0.1 µF NR：µ

把它当成 2.5 V 全幅正弦的参考：

有 NR 时：

全幅正弦的 rms ≈ 2.5 / (2√2) ≈ 0.88 V

SNR ≈ 20·log₁₀(0.88 / 4.5 µV) ≈ 108–109 dB

等效 ENOB ≈ (SNR – 1.76)/6.02 ≈ 17.8 bit

没 NR 时：SNR 掉到 ~104 dB，ENOB ~17.0 bit。

在 10 kHz 这样比较宽的带宽下，这颗基准本身可以支撑接近 18 位的系统动态范围，再往上就要靠 ADC 自己的数字滤波、OSR 来压噪声了；但是对几十 kHz 以内带宽的 16–18 bit SAR、20-bit 左右 ΔΣ ADC，当引入 NR 电容时，参考噪声基本不会成为主导瓶颈。

如果系统带宽只有 100 Hz、10 Hz 级，积分噪声会更小——参考完全足够 20 bit 等级的应用。（下面会讨论一个极端情况）

长期稳定性 / 老化

数据表给出：11 ppm / 1000 h 典型长期漂移（25 °C 连续工作）。

对 2.5 V 来说：

11 ppm 对应电压变化：2.5 V × 11 ppm ≈ 27.5 µV / 1000 h

换算成 ADC LSB 感觉一下：

16 bit，FS = 2.5 V：LSB ≈ 38 µV → 漂移 < 1 LSB/1000 h

20 bit：LSB ≈ 2.4 µV → 大约 11–12 LSB/1000 h

24 bit：LSB ≈ 0.15 µV → 这时任何基准都要配合周期性校准，单靠“绝对不漂”是不现实的。

注意啊！！！

这是典型值，而不是保证值，而且长期漂移往往是“对数时间”的：前几百小时漂得多，后面趋于慢慢变平，数据表的长稳图上也是这种形状。另外这个数是 纯器件 + 良好 PCB 条件下测出来的；实际系统里，板子应力、焊接应力、温度循环、湿度都会再增加几到几十 ppm；但是话说回来这颗芯片用的是气密陶瓷 LCC 封装，专门为了改善湿度和机械应力引起的漂移，比常规塑封要好一大截。

看这个结果做 16 bit 以内精度（工业控制、电源、一般仪器），这颗的长期漂移基本可以当“不存在”，一年级别的误差比温度漂和系统误差还小。但是做 20 bit 以上“标准仪器/计量级”时，它属于“不错，但还不是神仙”的水平：可以作为主基准，应该是需要上电预老化几个星期后再做“出厂标定”；如果非常的有钱也可以系统里保留周期性自校手段（比如用比对源或多路基准互测）。

NR 电容到底做了什么？

结构上它是个“内部节点的 RC 低通”

数据表 Pin 描述：NR = Noise Reduction，引脚 1，推荐接 0.1 µF 电容到 GND，用来改善宽带噪声。

“在 NR 上加 0.1 µF，可以把 1 kHz 处噪声从 75 nV/√Hz 降到 45 nV/√Hz，同时改善瞬态 PSRR；用 NR 电容测得的 0.1–10 Hz 噪声是 1.45 µV。”

可以把内部想象成这样：

核心 bandgap / buried-Zener 节点本身有噪声；这个节点通过内部放大电路（缓冲 + LDO 结构）驱动 OUT；NR 引脚把这个“参考节点”拉出来一部分，允许你在它和地之间加一个电容；内部在该节点前串了一个电阻 R，加上 C 后，形成一个 RC 低通：

低于 的 DC 和低频信号通过，高于 的噪声被衰减。

NR 脚其实是接到了内部参考放大器的某个“噪声敏感节点”，对地加 CNR 就是在那个节点挂了一个 RC 低通：低频 DC，不受影响，输出电压不变；如果是中高频噪声：被这个 RC 滤掉 → 所以宽带噪声密度明显下降（75 → 45 nV/√Hz）；同时，这个 RC 也会 改善 AC PSRR，高频的电源纹波，被这个节点的低通滤掉一部分，不再那么容易变成参考输出上的噪声。

它主要滤的是“参考内部的宽带白噪声”和通过电源耦合来的高频噪声；0.1–10 Hz 这类 1/f 噪声基本在 R 之前产生，对 C 不敏感，所以看到 0.1–10 Hz 噪声接不接 NR 差别不大。

实际选值和用法建议

官方推荐 0.1 µF，几乎所有典型曲线和指标都是按这个值给的；不建议太大（>0.1–0.22 µF）：带来的噪声改善有限，但启动时间会进一步变长（线性放大到几十毫秒以上）。这个节点阻抗较高，又直接影响基准噪声，建议 C0G / NP0 小容量瓷片，漏电和压电效应都比较小；也可以用 PPS、PTFE 小薄片电容，前提是体积允许；NR 引脚走线尽量短，直接贴在芯片旁边；参考地干净，不要穿过大电流回路；如果板子上有模拟地岛，把 NR 电容的地脚直接打在这个岛上。

代价：上电时间变长

CNR 和内部那个电阻共同决定一个时间常数 τ：

CNR 越大，上电时这个节点要充电的时间越长;手册给典型值：CNR = 0.1 µF 时，上电到 0.01% 需要 ~20 ms，不接时 ~1 ms。

如果系统带宽很窄（比如后端 ΔΣ ADC 数字滤波带宽只有几十 Hz），而且电源已经做得很干净，NR 即使用也只是锦上添花；对“超快上电、上电立刻校准”的系统（比如某些便携设备上电后几毫秒内要采样）可以权衡：不要 NR → 噪声略高一点，但启动超快；大多数高精度测量系统还是建议焊上 0.1 µF，因为 20 ms 的上电时间通常完全可以接受。

另外对大多数精密系统，这 20 ms 完全可以接受，所以我的建议是：

作为精密基准使用：NR=0.1 µF 视为“必配”，除非有特别苛刻的上电瞬态要求。

继续算一个极端案例

按32bit ADC 带宽 100k，算一遍“基准噪声 → 系统 ENOB”占比，看看我们在具体信号链里它到底是不是瓶颈。

先把这颗 MAX6226 的噪声 & 稳定性参数拎出来

数据手册给的关键数字（以 2.5 V 版本为例）：0.1–10 Hz 低频噪声， （NR=0.1 µF 时测得）

宽带噪声密度 @1 kHz：

无 NR：75 nV/√Hz

NR=0.1 µF：45 nV/√Hz（2.5 V 输出）MAX6226

长期稳定度（长期漂移）： （典型值）

温度系数：A 档 1 ppm/°C 典型，3 ppm/°C 最大

热滞回：约 5 ppm/全温度循环

把这些换算成立即有用的“电压量级”：

以 2.5 V 参考为例：

长期漂移 11 ppm/1000 h → 电压，

热滞回 5 ppm → 电压，

温漂 3 ppm/°C（max）

若只在 25 ± 10 °C，小范围变化： 总温漂 ≈ 3 ppm/°C × 20 °C = 60 ppm → 150 µV；如果真跑满 -40~+125 °C（165 °C），那是 495 ppm ≈ 1.24 mV（这是“极端 worst-case 量级”）。

结论： 这颗基准的长期漂移和热滞回都是几十 µV 级别， 对 2.5 V 参考来说，相当于 10⁻⁵ 量级的长期相对变化。

在 100 kHz 噪声带宽下评估：配 32-bit ADC 会怎么样？

给的条件：100 kHz 带宽 + 32 位 ADC，我们先单独算“参考噪声本身能支撑多少 ENOB”。

以 NR=0.1 µF、2.5 V 版本为例：

参考噪声积分（BW = 100 kHz）

宽带白噪声部分

假设在 0–100 kHz 内近似白噪声：

0.1–10 Hz 低频噪声部分

1.45 µVpp，按常见经验 反推：

合成参考噪声（RMS）

低频那一小点可以忽略不计——100 kHz 里完全是白噪声在主导。

折算成“参考决定的 SNR / ENOB 上限”

假设 ADC 满量程正弦，振幅 = ：

折算成 ENOB（常用公式）：

在 100 kHz 有效噪声带宽下，这颗基准本身就把系统 ENOB 限制在 ~16 bit 左右（即使 ADC 做到理想 32 bit）。

如果 BW 只到 10 kHz，白噪声会变成：

同样算一遍，会得到：

10 kHz 带宽 → ENOB ≈ 17.8 bit

1 kHz 带宽 → ENOB ≈ 19.4 bit

也就是说：

带宽每减一位数量级，参考噪声限制的有效位数大概多 1–2 位。

和“理想 32-bit ADC”对比一下直觉

理想 32 位 ADC 的理论 SNR：

而我们算出来的 参考限制 SNR 只有 ~99 dB，中间差了将近 100 dB（相当于 16 bit 的差距）。

所以一个现实判断是：在 100 kHz 带宽下，即便挂的是“32-bit ADC”， 在 MAX6226 做参考的情况下，系统能看到的有效位数 也就是 16 bit 上下，更窄带宽可以到 18–19 bit。

这还是“只算参考噪声”的结果，没有把 ADC 自身噪声、前端放大器、PCB 噪声等加进去——现实系统会再打折。

长期稳定性对“绝对精度位数”的限制

再看长期漂移：

11 ppm/1000 h → 对应电压约 27.5 µV/1000 h

这个相对误差 ≈ ，等价位数 ≈

解释一下这句话的含义：

不做任何周期校准的情况下，“绝对电压准确度”长期只能稳定在 ~16.5 bit 的水平， 再高的位数都会被几十 µV 级的长期漂移“淹掉”。

如果愿意定期做标定/存储温度曲线，就可以把长期漂移从“系统误差”变成“可补偿项”，那样就可以利用到更多的瞬时 ENOB（比如 18–19 bit）。

仿真

   Noise BW (Hz)  White RMS (no NR) [nV]  Total RMS (no NR) [nV]  \
0             10              237.170825              323.290517   
1            100              750.000000              781.515680   
2           1000             2371.708245             2381.862036   
3          10000             7500.000000             7503.217094   
4          50000            16770.509831            16771.948806   
5         100000            23717.082451            23718.099982   

   SNR limit (no NR) [dB]  ENOB limit (no NR) [bits]  \
0              131.746341                  21.592415   
1              124.079446                  20.318845   
2              114.399868                  18.710942   
3              104.433250                  17.055357   
4               97.446530                  15.894772   
5               94.436602                  15.394784   

   White RMS (NR=0.1uF) [nV]  Total RMS (NR=0.1uF) [nV]  SNR limit (NR) [dB]  \
0                 142.302495                 261.757060           133.580232   
1                 450.000000                 500.766171           127.945501   
2                1423.024947                1439.884286           118.771648   
3                4500.000000                4505.359781           108.863611   
4               10062.305899               10064.704007           101.882180   
5               14230.249471               14231.945291            98.872915   

   ENOB limit (NR) [bits]  
0               21.897049  
1               20.961047  
2               19.437151  
3               17.791297  
4               16.631591  
5               16.131713  

一个表：MAX6226: Reference noise vs bandwidth (up to 100 kHz)

图 1：积分参考噪声 vs 带宽

图 2：参考噪声能支撑的 ENOB 上限 vs 带宽

我用的数据就是手册里的:(宽带噪声密度：75 nV/√Hz（NR 不接）,45 nV/√Hz（NR=0.1 µF）;0.1–10 Hz：1.45 µVpp 低频噪声。)

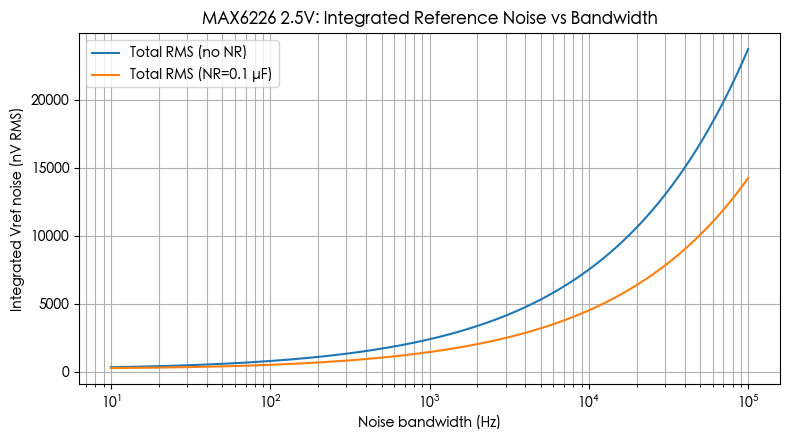
横轴：噪声带宽（10 Hz → 100 kHz，log）

纵轴：积分后的参考噪声（nV RMS）

蓝线：NR 不接，橙线：NR=0.1 µF

带宽越大，噪声越 √BW 地往上爬;NR 线（橙色）一直比蓝线低，大带宽时差距越来越大 → 说明 NR 对高带宽系统更有价值

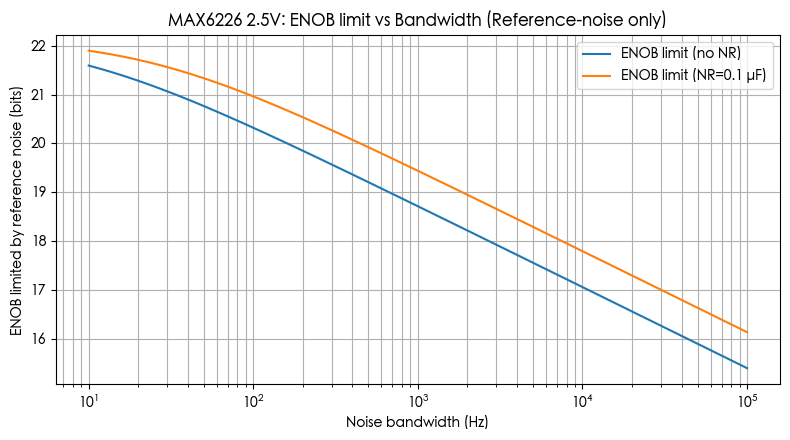
横轴：噪声带宽

纵轴：仅由参考噪声决定的 ENOB 上限

会直观看到：

10 Hz 带宽时：

有 NR：~21.8 bit

无 NR：~21.5 bit

100 kHz 带宽时：

有 NR：~16.1 bit

无 NR：~15.3 bit

在实际做的高分辨率低频测量（比如 1 kHz、几十 Hz 的 ΔΣ 带宽）里：参考噪声能支撑的 ENOB 远大于 ADC 实际 ENOB，MAX6226 完全够用，NR 电容属于“锦上添花级”。