从几何独立性到拓扑实现：单纯复形在生成式AI与具身智能中的理论架构分析

从几何独立性到拓扑实现：构建未来人工智能与具身智能的几何引擎

走向未来

在当今这个算力爆炸与智能涌现的时代，我们往往沉迷于参数量的指数级增长和模型架构的日新月异，却容易忽视支撑这一宏伟数字大厦的深层地基。最近正好阅读了一篇纯粹的论文《单纯复形基础：从几何独立性到实现》（该论文已收录至“走向未来”知识星球中），从该文严谨的逻辑构建了从离散点集到连续几何空间的完整映射，这恰恰揭示了当前人工智能从感知走向认知、从数字世界走向物理世界的关键路径。

3.jpg

我们首先需要重新审视数据的本质。在文件中，欧几里得空间被定义为所有数学构造的舞台，这正是我们在人工智能中处理的高维向量空间。对有限维和无限维欧几里得空间的精确定义，不仅是几何学的起点，也是我们理解现代大模型嵌入空间的公理化基础。在生成式人工智能中，无论是文本、图像还是视频，以及其他各类数据，最终都被转化为高维空间中的点。每一个数据样本，无论是莎士比亚的十四行诗还是波士顿动力机器人的传感器读数，在数学的眼光下，都是RN空间中的一个点。这些点集构成了向量空间、赋范空间和度量空间，这三个层次恰好对应了AI模型中的特征表示、相似度计算以及损失函数的优化基础。如果不理解欧几里得空间的度量性质，我们就无法设计出有效的注意力机制来捕捉长距离依赖；如果不理解拓扑空间的开集概念，我们就难以理解模型泛化能力的边界。因此，重温这些基础定义，实际上是在校准我们对特征空间这一核心概念的认知精度。

213.jpg

在这之上时几何独立性概念，这为我们评估数据质量和模型效率提供了一个绝佳的数学视角。例如，一个点集的几何独立性等价于其相关向量的线性独立性，并给出了通过矩阵秩来判定的具体工作法则。这在机器学习中具有极高的指导价值。我们在训练大模型时，常常面临维数灾难和特征冗余的双重挑战。几何独立性的概念告诉我们，并非所有的数据点都能撑起一个有效的几何结构。如果一组数据向量在几何上不是独立的，那么它们所张成的空间维度就会坍塌，这意味着模型在这些方向上无法学习到有效的区分度。另外，由几何独立集张成的n维平面，这直接对应于流形学习中的局部切空间概念。如果我们能够保证采样点在局部保持几何独立，那么我们就能更精准地重构出数据流形的内在结构，这对于理解提升生成式模型的逼真度和多样性至关重要。

2.jpg

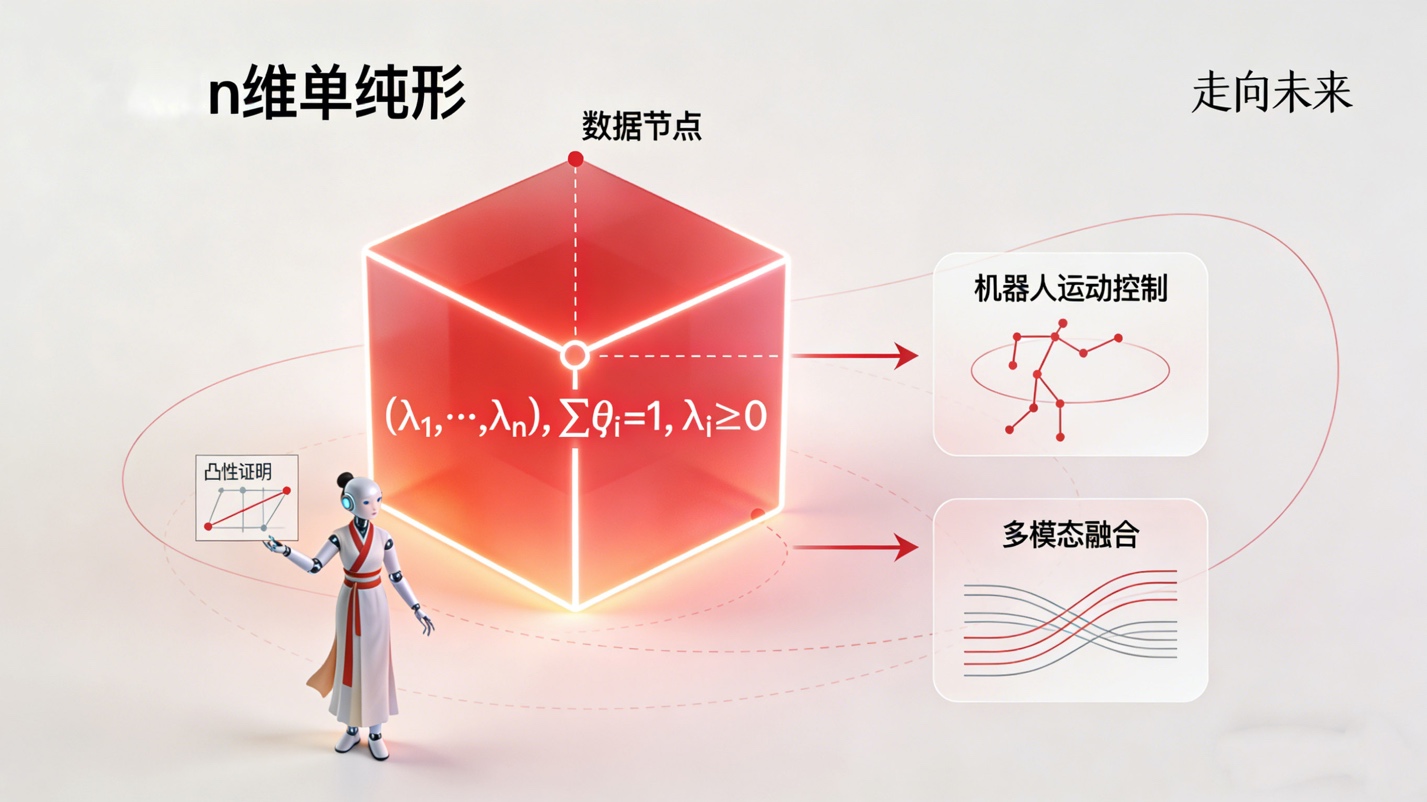
在此基础上，单纯形作为几何独立点的凸包，构成了连接离散数据与连续空间的原子单元。文件中对单纯形的凸性、紧致性以及重心坐标的连续性进行了详尽的证明，这些性质在机器人学和智能体路径规划中具有不可替代的物理意义。凸性保证了我们在单纯形内部进行插值时，结果永远不会跑出这个几何形状的范围，这对于保证机器人运动控制的稳定性至关重要。想象一下，一个具身智能机器人需要在复杂的非结构化环境中移动，我们将环境建模为一系列单纯形的组合。单纯形的凸性意味着，只要机器人处于某个单纯形内部，其状态就是可控且安全的。在大模型中，我们将不同模态的信息视为顶点，通过重心坐标进行加权融合，其连续性保证了模态切换过程的平滑，避免了感知跳变带来的决策失误。此外，文件指出的单纯形与单位球的同胚性，暗示了在高维空间中，复杂的局部几何结构可以通过连续变换映射为规则的球体，这为我们设计标准化流模型和扩散模型提供了拓扑学依据，使得我们能够在潜在空间中进行更高效的采样和生成。

1.jpg

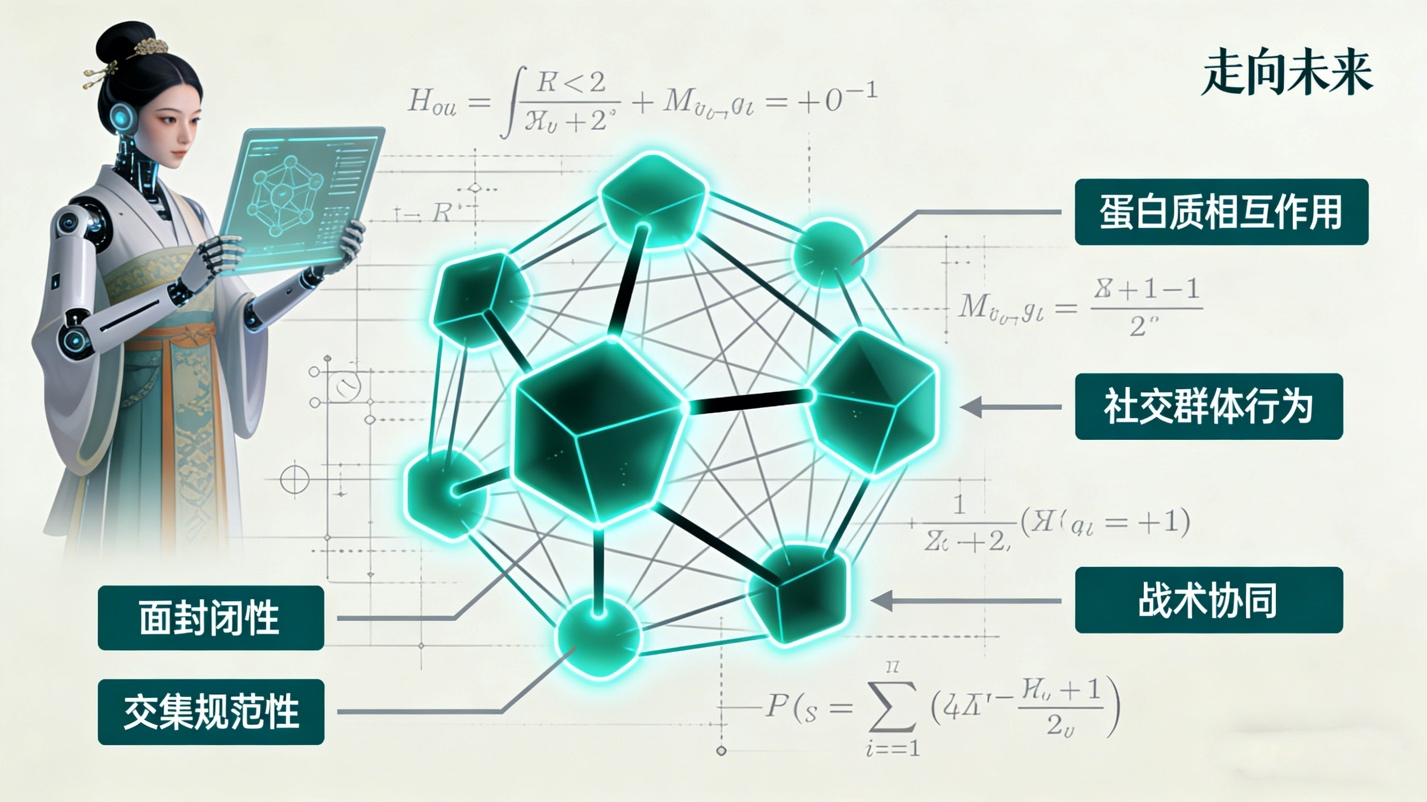
当我们将目光投向单纯复形时，我们看到的是从局部感知到全局认知的跃迁。单纯复形通常定义为单纯形的集合，要求其在面运算下封闭且交集规范。这一严格的代数拓扑定义，实际上描绘了知识图谱和神经网络的高阶形态。传统的图神经网络主要处理二元关系，即边连接两个节点。然而，现实世界的复杂系统，如蛋白质相互作用、社交网络群体行为以及战术协同，往往涉及多元的高阶交互。单纯复形允许我们将三个、四个甚至更多个节点通过面、体等高阶结构连接起来，形成比图更丰富的拓扑结构。不同单纯形的内部互不相交，则为我们构建高效的稀疏神经网络架构提供了理论约束。如果我们把神经网络的每一层看作是一个单纯复形，那么信息的传递就不仅仅是沿着边流动，而是可以通过面和体进行高维度的广播和聚合。这种基于单纯复形的网络架构，即单纯神经网络，极有可能是超越当前Transformer架构的下一代技术高地，它能以更少的参数量实现更强的逻辑推理和抽象概括能力。这有助于激发我们的创新。

几何实现及其拓扑性质则是将AI带入物理世界的关键一跃。几何实现将抽象的组合结构转化为具体的拓扑空间，赋予了离散符号以连续的物理形态。单纯复形的几何实现是豪斯多夫空间且局部紧致，这为机器人的仿真与现实迁移提供了数学保证。在仿真到现实的过程中，我们往往面临仿真环境与真实物理环境拓扑结构不一致的问题。通过单纯复形的几何实现，我们可以建立一个标准化的中间层，确保策略网络学到的运动流形在拓扑上是鲁棒的。特别是文件中关于星域和链接的定义，为局部感知和分布式控制提供了数学模型。对于一个在未知环境中探索的智能体，它不需要感知整个世界，只需要关注其当前位置的星域，即与其直接相邻的几何结构。星域的闭包是一个有限子复形的多面体，这意味着智能体可以在有限的算力资源下，对局部环境进行精确建模和决策。这对于边缘侧AI芯片的设计提出了明确需求，即硬件需要对稀疏的局部拓扑结构检索和计算进行专门优化，而不是仅仅堆砌全局矩阵乘法的算力。

4.jpg

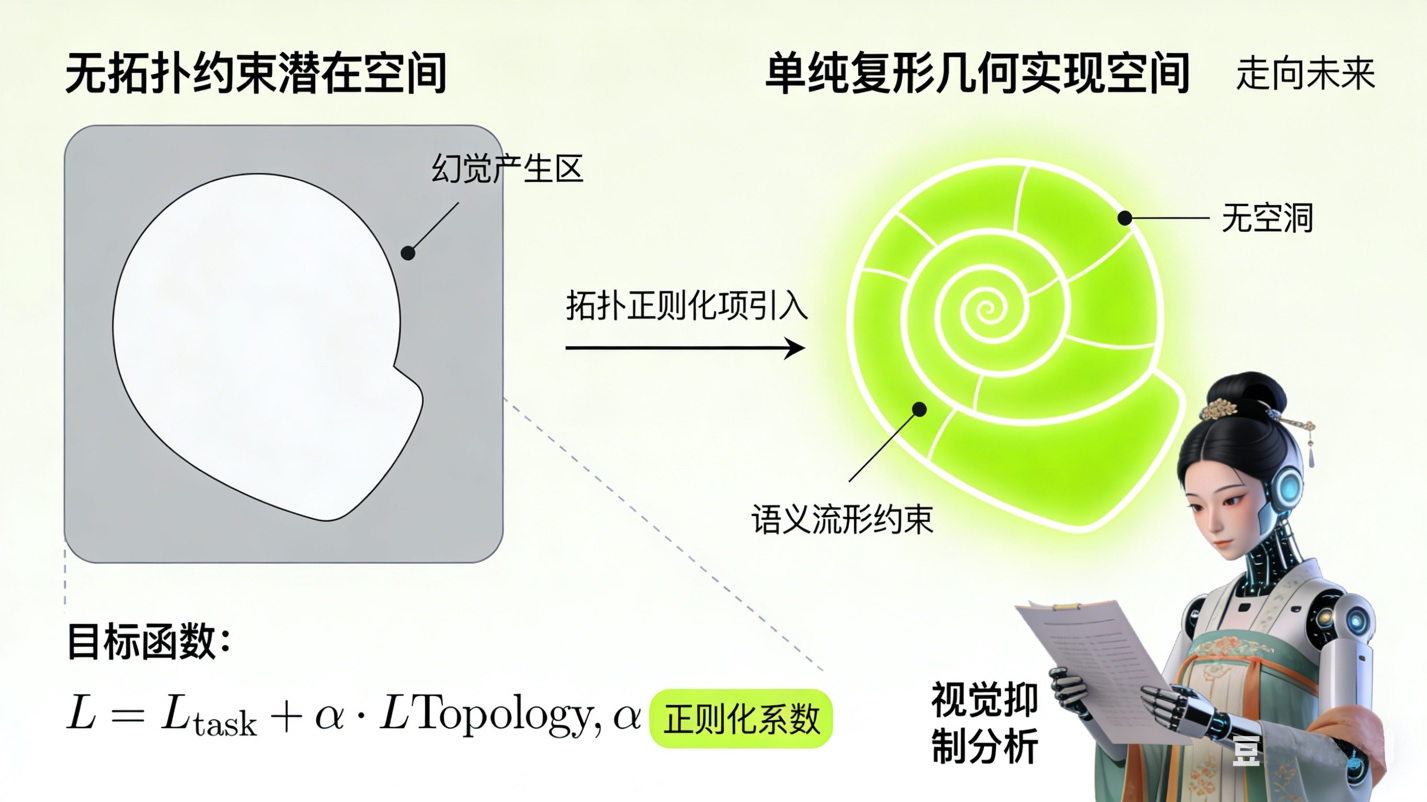
此外，关于单纯复形拓扑性质对于解决大模型的幻觉问题也提供了新的思路。我们知道，幻觉往往源于模型在潜在空间的空白区域进行了错误的插值。而单纯复形的几何实现要求所有单纯形通过面严丝合缝地粘合，这在拓扑上消除了空洞。如果我们能将大模型的潜在空间约束在单纯复形的几何实现上，那么所有的生成结果都将落在有效的语义流形内，从而从根本上抑制幻觉的产生。这需要我们在训练目标函数中引入拓扑正则化项，强制模型的特征分布符合单纯复形的结构约束。事实上，工程实践中的图模互补应用范式与这个思路有着异曲同工之妙。王文广在其灯塔书《知识增强大模型》中深刻剖析了图模互补的核心价值：利用图谱（Graph）的确定性与一致性来弥补大模型（Model）的概率性幻觉（第8章）。单纯复形在此基础上更进一步，它不再局限于二元关系的图谱，而是通过高维的单纯形构建起一个“高阶图谱”。这种几何结构不仅继承了知识图谱的可解释性与逻辑约束，更通过其几何实现的连续性（如重心坐标的平滑变换），完美适配了神经网络的梯度下降算法。

在市场价值和社会价值层面，单纯复形理论的工程化应用将带来巨大的经济效益。在自动驾驶领域，基于单纯复形的环境建模可以大幅减少对高精地图的依赖，使车辆具备像人类一样的拓扑导航能力，从而降低运营成本并提高系统在极端环境下的可靠性。在生物医药领域，利用单纯复形分析蛋白质折叠空间，可以发现传统几何方法难以捕捉的拓扑位点，加速新药研发进程。在金融风控领域，单纯复形网络能够识别出复杂的洗钱团伙和系统性风险传导路径，维护金融安全。这些应用场景的落地，不仅仅是技术的胜利，更是数学思维在产业界的价值变现。

面对如此广阔的产业前景和技术迭代，我强烈推荐加入最具价值知识星球“走向未来”。在星球中，您可以获取AI相关的各类市场分析报告、技术论文书籍、应用实践指南等等，主题涵盖生成式AI、大模型、AIGC、AI芯片和机器人等技术、应用和市场，并与同侪一起探讨如何使用人工智能大模型和智能体来为工作增效，为生活添彩。

实际上，数学是一个深入理解现代的AI的很好的工具，甚至可能是开启下一代人工智能大门的钥匙。因为，数学可以为我们提供了一套完整的语言，去描述高维空间的结构、去理解数据的形状、去构建具有物理常识的智能系统。从欧几里得空间的点集到几何独立的单纯形，再到结构严谨的单纯复形及其连续的几何实现，这一条数学演进的路径，正是我们构建更加鲁棒、可解释且高效的智能系统的必由之路。作为行业从业者，我们应当积极拥抱这种底层的数学思维，将其融入到算法设计、芯片架构以及产品定义的每一个环节中。

最后，该论文还探讨了凸集和放射变换等。凸集为优化算法的设计指明了方向。目前的梯度下降法在非凸的损失函数曲面上容易陷入局部最优。如果我们将参数空间重新参数化为单纯复形的几何实现，利用其局部凸的性质，我们或许可以设计出一种组合优化与连续优化相结合的新型算法。仿射变换的探讨则提醒我们在处理机器人视觉和操作任务时，必须重视几何不变性。仿射变换保持了共线性和比例关系，这是机器人在不同视角下识别物体和规划抓取动作的基础。这对于设计未来的家用服务机器人能够提供一定的帮助，例如无论从哪个角度观察，都能准确地认出桌子上的水杯并完成抓取。

总结来看，在未来的技术演进中，单纯复形将成为连接离散符号与连续物理世界的桥梁，成为构建可解释、鲁棒且高效智能系统的核心引擎。无论是对于致力突破技术瓶颈的研究人员，还是对于寻求产业升级的企业家，深入理解和应用这一理论，都将在未来的智能革命中占据先机。

388.jpg