大模型｜MoE混合专家系统介绍

大模型的MoE架构日益流行，其利用路由发送特定数量的token到不同的专家，并聚合专家结果，得到同等参数量下相比稠密模型更优的效果，且冗余计算少性能更优。但其发展也面临诸多问题，本文主要探讨下MoE的稀疏性特性和负载不均衡问题。

1, MoE模型架构中路由器和专家系统介绍 2, 专家系统中稀疏性的公式推导和具体的推理流程介绍 3, MoE系统中专家负载不均衡问题的解决方案探讨

1，MoE原理介绍

MoE定义：将传统 Transformer 模型中的每个前馈网络(FFN) 层替换为MoE层，就构成了混合专家系统，其中MoE 层由两个核心部分组成：一个路由门控网络和若干数量的专家系统。

1.1，MoE系统构成

• • 路由门控网络 功能：根据输入特征，动态地分配每个token到最合适的专家。 构成：通常是一个小的神经网络，或是全连接层或轻量级的神经网络结构。 训练：参数可学习与网络的其他部分一同进行预训练。通过反向传播，路由器的参数不断调整，优化token的分配策略。
• • 专家系统 功能：每个专家负责处理分配给它的token，能够针对不同类型的输入提供专门的处理能力，从而提高模型的整体性能。 构成：前馈网络 (FFN)或其他类型的神经网络结构。每个专家可以有不同的参数和架构，以适应不同的任务需求。 训练：其参数与门控网络一同进训练，通过反向传播，每个专家的参数不断优化，以最小化整体损失函数。训练过程中，专家系统会逐渐学会处理特定类型的输入，从而提高模型的泛化能力和性能。

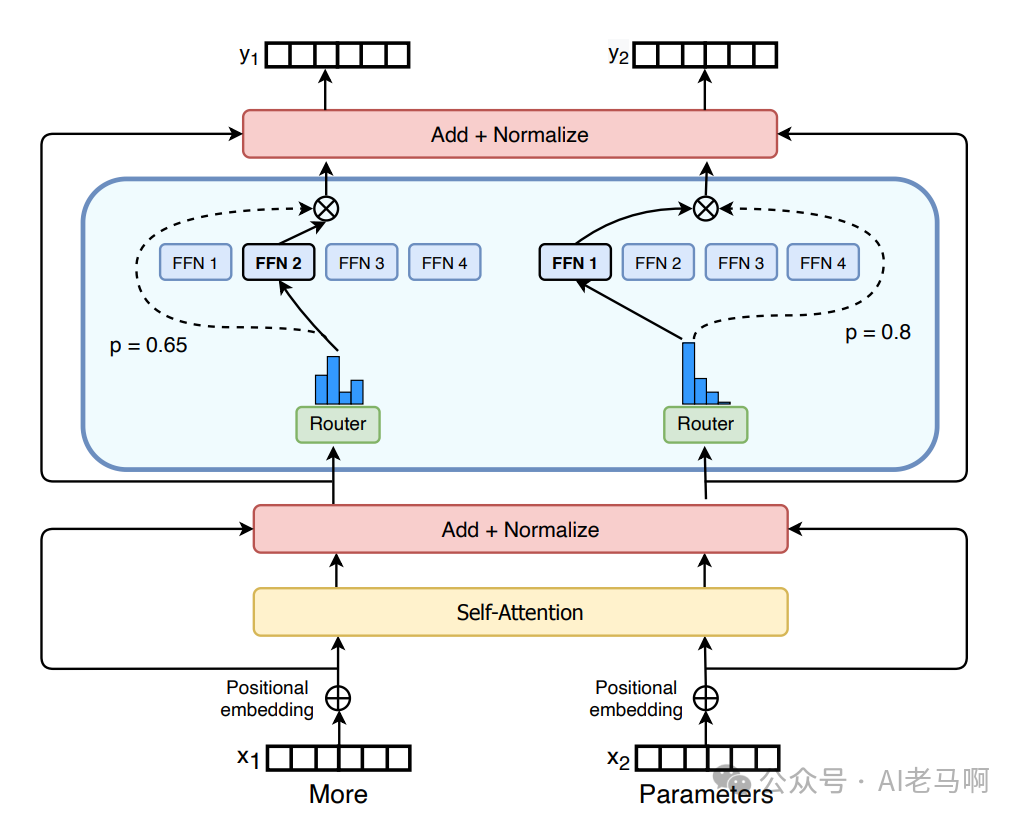
图1，混合专家系统MoE示意。

1.2，MoE 中的稀疏性

MoE系统具备的稀疏性，使得模型在训练和推理时，使用少量的计算资源，就可以完整摸型计算，而效果与稠密模型持平。

• • 稀疏性定义：

稀疏性的概念采用了条件计算的思想，稀疏性允许仅针对整个系统的某些特定部分执行计算，并非所有参数都会在处理每个输入时被激活或使用，而是根据输入的特定特征或需求，只有部分参数集合被调用和运行。

• • 条件计算的概念

即仅在每个样本的基础上激活网络的不同部分，便在不增加额外计算负担的情况下扩展模型规模成为可能。

利用稀疏性扩大模型规模，模型规模是提升模型性能的关键因素之一。在有限的计算资源预算下，用更少的训练步数训练一个更大的模型，往往比用更多的步数训练一个较小的模型效果更佳。

• • 公式定义

公式1，表示N个专家系统的求和过程。公式2，是路由器的具体计算过程。W表示路由权重矩阵，由softmax处理后获得样本x，被分配到每个expert 的权重，然后只取前 k 的最大权重。

1.3，推理流程示例

假设输入数据，batch=2，seq=5，hidden_size=128。

有四个专家，即e=4，选取排名靠前的两个专家，即topk=2，每个专家同时可处理5个token，即expert_capacity=5。

在理想情况下，输入数据共有2*5=10 token，topk为2时，每个token被分配到2个专家，此时正好满足所有专家需求 4*5=20。但是路由的分派不一定是均衡的，就造成了负载不均衡问题。

2，MoE token负载不均衡问题

2.1，优化思路和名词介绍

在混合专家模型训练中，门控网络往往倾向于主要激活相同的几个专家，这种情况可能会自我加强，因为受欢迎的专家训练得更快，因此它们更容易被选择。如果所有的令牌都被发送到只有少数几个受欢迎的专家，导致每个专家分配到的token数量是不平均的，那么训练效率将会降低。

优化思路有两个方向：

• • 调整路由分配策略，尽可能的将token均分到每个专家系统 [1]
• • 既然token在每个专家上数量不均，通过块稀疏计算，使并行批量计算正常进行 [2]

专家容量和容量因子

• • 专家容量 Expert Capacity：每个专家能够处理的最大token数量。
• • 容量因子 Capacity Factor：扩大专家容量的因子，可以看做是减少丢弃token的超参数。
• • 容量计算公式，对于包含E个专家的MoE层，每个专家的容量上限为：

实际中，容量因子为全局超参数（通常设为1.0-2.0），Batch Size 训练或推理的批次大小，Sequence Length输入序列长度，E专家数量。从公式可以看出，如果容量因子为1，每个专家的容量为总的token均分到每个专家系统，如果大于1，则每个专家有一定的容量buffer，可以处理被多分配的oken 数量。

2.2，方案一：动态调整专家容量

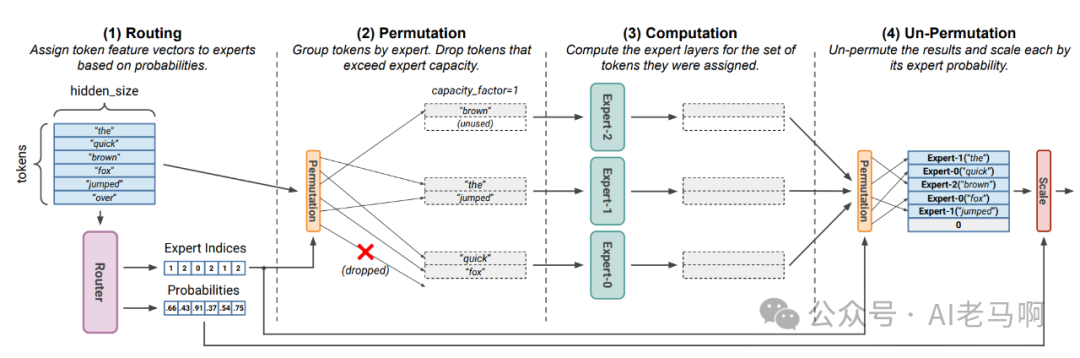
图2，通过调整专家容量解决负载不均衡问题。

核心思想：通过调整容量因子超参，动态的调整专家容量，这样每个专家有更大的能力处理多余的token数量。

局限：

• • 容量因子越大，被丢弃的token数量越少，但padding数量增加，浪费GPU计算资源。
• • 如果存在被丢弃的token，只能通过残差网名进行弥补，而实验表明，丢弃token数量一定程度上会影响最终模型的效果。

还有其他的一些路由策略：比如负载感知路由分数调整，在路由的分数中引入负载反惯，动态调整专家选择概率。Sinkhorn双归一化路由将路由过程建模为最优传输问题，使用Sinkhorn算法对路由矩阵进行，行（token）和列（专家）的双归一化。

2.3，方案二：块稀疏对角矩阵运算

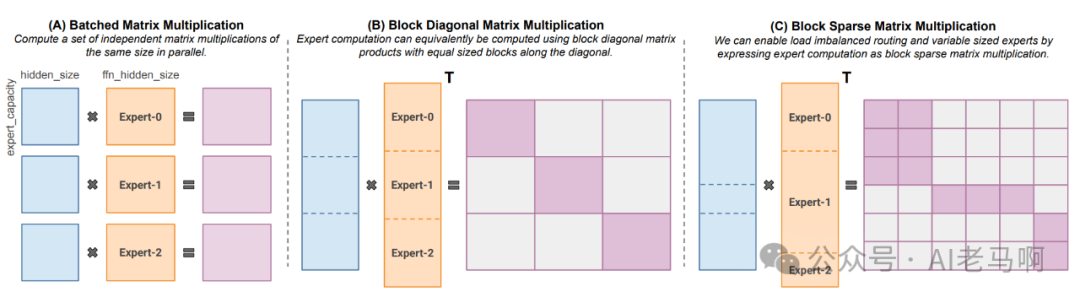
图3，块稀疏对角矩阵解决负载不均衡问题。

上图A中，每个专家的负载是一致的，可利用并行矩阵运算提升计算效率。如果每个专家分配到的token不均衡，通用的并行策略无法使用，需要通过稀疏的块对角矩阵完成。

• • 方式 A：批量矩阵乘法（强制负载均衡）

如果GPU上分配了E个专家，一个最简单的办法就是执行E次串行的GEMM就可以。但是这样GEMM之间没有并行，GPU利用率不高。并行的把E个矩阵乘法一起算，也就是Grouped GEMM。其核心是 “将多个同维度的小矩阵运算，打包成一个批次的并行任务”，适配 GPU 的批处理硬件架构（如 NVIDIA 的 Tensor Core）。

计算过程：

输入分配：总 token 交互数为10×2=20，平均分给 4 个专家，每个专家接收20/4=5个 token，得到每个专家的 5 个输出（维度5×128）。

矩阵构造：每个专家权重W_i(128,128)，堆叠为批量权重矩阵W_batch=[W1, W2, W3, W4](128, 4×128)（横向拼接 4 个专家权重）。

并行计算：输入按专家分组，每组 5 个 token，拼接为(20, 128)的矩阵，与W_batch相乘，X_grouped(20,128) × W_batch(128,512) = (20,512)直接得到所有专家的输出。

GPU 会将 E 个小矩阵运算分配到不同的 SM 上同时执行，每个 SM 独立处理一个专家的 GEMM，无需等待其他专家完成。此时所有 SM 都处于满负载状态，计算效率接近理论上限，这也是负载均衡时 MoE 的最优并行方案。

• • 方式 B：等尺寸块对角矩阵乘法

核心逻辑：将计算抽象为块对角矩阵，块尺寸由 “每个专家的固定 token 数” 决定，与方式 A 等价，仅矩阵结构不同。

计算过程：

输入分配：与方式 A 一致，每个专家接收 5 个 token，输入拆分为 4 个等尺寸块X1~X4（每个5×128），X = [X1; X2; X3; X4]（纵向拼接，20×128）。

矩阵构造：构建块对角矩阵W_block = diag(W1, W2, W3, W4)，对角块依次为W1~W4（每个128×128），非对角块为 0。

并行计算：输入矩阵于对角矩阵相乘，X × W_block = [X1×W1; X2×W2; X3×W3; X4×W4]，每个块Xi仅与对应Wi计算，输出(20,128)，结果与方式 A 完全一致。

• • 方式 C：可变尺寸块对角矩阵乘法（块稀疏矩阵）

核心逻辑：按路由分数动态分配 token，允许专家接收不同数量的 token，通过块稀疏矩阵实现高效计算。

计算过程：

输入分配：根据路由分数，每个 token 选择 2 个专家，最终专家接收的 token 数可能不同。如专家 1 接 5 个 token（X1:5×128），专家 2 接 6 个（X2:6×128），专家 3 接 4 个（X3:4×128），专家 4 接 5 个（X4:5×128）总和5+6+4+5=20。注意专家 2 超容量时需截断或重分配，此处假设容量足够。

矩阵构造：构建块稀疏矩阵W_sparse，构建块对角矩阵W_sparse = diag(W1, W2, W3, W4)，对角块依次为W1~W4（每个128×128），非对角块为 0。

并行计算：仅计算输入块与对应专家块的乘积（跳过零块），最终拼接输出。[X1; X2; X3; X4] × W_sparse = [X1×W1'; X2×W2'; X3×W3'; X4×W4']，输出维度20×128。

详细的过程可以参考下，Megablocks[2]。

2.4，方案三：可微分的负载均衡损失

核心思想：引入辅助损失，鼓励给予所有专家相同的重要性，确保所有专家接收到大致相等数量的训练样本，从而平衡专家之间的选择。

以上问题的根源是，路由不能均分token到每个专家系统，那在损失中加入乘法因子，鼓励其均分token。加入损失有很多种，比如在 switch transformer[1] 中作者加入了一种可微分的负载均衡损失。

3，MoE系统优势和局限

• • 预训练速度更快，且有更快的推理速度。

具有相同参数量的稠密模型和MoE模型，在训练和推理时，MoE模型具有明显优势。因为每次计算只有少数的专家系统被激活，而不是全部的参数。这样计算量降低，相应的训练和推理时间也减少了。

• • 所有专家都需要加载到内存中，需要大量显存

从另外角度，推理时，只用到少量的专家系统，但是必须加载全部的专家到内存中，对内存消耗巨大。

• • 稀疏VS稠密，如何选择?

稀疏混合专家模型适用于拥有多台机器且要求高吞吐量的场景。在固定的预训练计算资源下，稀疏模型往往能够实现更优的效果，相反，在显存较少且吞吐量要求不高的场景，稠密模型则是更合适的选择。

• • 阻碍MoE模型大规模流行的原因有那些?

虽然MoE模型在同量级模型中，训练和推理速度快，但是面临个三个主要的问题：1) 模型复杂度，2) 训练稳定性 ，3) 通信开销大

参考：

[1] arXiv:2101.03961 [2] arXiv:2211.15841