向量：AI时代的技术基石——从数学本质到工程实践

在当今的技术世界中，"向量"这个词汇正以前所未有的频率出现在各种技术场景中：从机器学习的特征表示到图形学的几何计算，从数据库的新型存储范式到搜索引擎的语义理解。但究竟什么是向量？为什么它能在人工智能时代成为如此关键的技术基石？本文将从技术人员的视角，深入剖析向量的本质、数学原理、计算优化和实际应用，揭示这一概念如何从基础的数学工具演变为现代计算的核心支柱。

本文目标：

• 第一部分希望你对向量有一个直观的感受
• 第二部分希望你能对向量数据库有一个整体的认识

向量的本质：超越几何的技术抽象

大约公元前350年，古希腊著名学者亚里士多德就知道了力可以表示成向量，两个力的组合作用可用著名的平行四边形法则来得到。"向量"一词来自力学、解析几何中的有向线段，最先使用有向线段表示向量的是英国著名科学家牛顿。向量能够进入数学并得到发展。

同样在机器学习中，向量也是被广泛使用的。

从数学定义到技术实现

在经典数学中向量被定义为"既有大小又有方向的一组数字"。然而在技术领域，有着更加实用和抽象的理解：

向量 = 有序数值数组 + 运算规则

这个简单的公式概括了向量在计算系统中的本质：它既是一种数据结构，也伴随着一套完整的运算体系。

特别注意： 一组有序的数值数组一定是向量，但一个数组不一定是向量。这一区别的关键在于是否定义了相应的向量运算规则。数组是存储结构，而向量是带有语义和运算规则的数学模型。

现代计算中向量的演化

在现代计算范式中，向量的概念已经远远超出了传统的几何范畴：

特征向量（Feature Vector）

机器学习中的数据表示，将现实世界对象编码为有序数值特征。通常用于一个固定的群体中去发现异常。

示例：水果分类

• 颜色（用"红度"和"黄度"表示，0-10分）
• 形状（越接近球形分数越高，0-10分）
• 长度（单位：厘米）
• 表皮光滑度（越光滑分数越高，0-10分）

苹果：[9, 1, 8, 7, 8]

• 红度：9 （很红）
• 黄度：1 （基本不黄）
• 形状：8 （比较圆）
• 长度：7 cm
• 光滑度：8 （表皮光滑）

香蕉：[1, 9, 2, 18, 6]

• 红度：1 （基本不红）
• 黄度：9 （很黄）
• 形状：2 （长条状，一点也不圆）
• 长度：18 cm
• 光滑度：6 （有一定弧度，但不如苹果光滑）

通过向量，两者非常方便的区分出来。简单的也可以理解为，通过向量，数字把"一个红红的圆苹果"表达出来。

在特征向量中，更强调数据的规一化（统一数据加工方法），让数据变的有规则一点。这个方式在以前搞过机器学习的人眼里已经非常熟悉，可能只是对数据库人员有点陌生。

如果大概理解了这一点，你就可以开始机器学习的 Hello World：Iris 鸢尾花数据集探索了。

嵌入向量（Embedding Vector）

自然语言处理中的语义编码，为各类信息（文本、图像、声音等）生成一个"数字身份证"。这个身份证不是简单的编号，而是一串有意义的数字，能表示这段文字的特征和含义。

示例：猫的 Embedding Vector

向量坐标（简化版）：

[宠物感: 0.92, 毛茸茸: 0.88, 独立性: 0.85, 体型小: 0.60, 喵叫: 0.95, 犬科性: -0.90, 翅膀: -0.99, 水生: -0.98, 家具: -0.30, 忠诚度: 0.40...] 768 维

实际存储的向量数据为：

[0.92, 0.88, 0.85, 0.60, 0.95, -0.90, -0.99, -0.98, -0.30, 0.40...] 768维

Embedding Vector 模型也是当红炸子鸡，随着大模型的出现，各种知识库的出现，基本都是：Embedding Vector + Query Vector 组合。

这里面，其实也考验分词和句子拆分，私有名词的指定，甚至需要结合全文检索来使用。

实际项目中的挑战： Embedding 模型升级后，造成生成的向量不一致（失效），就会面临大量的向量更新的问题。这些方面可以查看 OpenAI 及 Google 对外公开的滚动升级方案，不管怎么说这是一个大动作。

查询向量（Query Vector）

搜索引擎中的语义查询表示，一种特殊化的嵌入向量。查询向量是指把用户的问题向量化，属于 Embedding 中的一种。

状态向量（State Vector）

强化学习和物理仿真中的环境状态描述，强调动态系统的瞬时状态。状态向量本质上也是一种特征向量，属于特征向量中的一种。状态向量通常指物体在物理系统中的描述。

示例：鸟的飞行相关数据

[速度，高度，GPS位置，温度，湿度，风速,...]

第一部分总结： 对于科普什么是向量，到这里就可以了，如果你对向量数据库感兴趣，可以继续往下面看。

向量索引

向量本身是一个高维数组，直接检索需要大量的计算，这就引出了向量索引。向量索引就是给高维数据做"地图"，先画几个大区，再画小区，查的时候按图索骥，秒级找到"最像"的几个点，而不是一条一条的比较。

技术要点：

• HNSW：通过多层图结构实现快速导航，从高层粗粒度定位到底层细粒度搜索
• IVF：先将数据聚类到多个桶中，搜索时只检查最相关的几个桶
• LSH：将相似向量以高概率映射到相同哈希桶，实现近似搜索
• FLAT：直接计算查询向量与所有向量的距离，保证结果完全准确

向量检索

向量检索是一种通过将数据（如文本、图片、音频）转换为高维空间中的向量，并通过计算向量之间的距离或相似度，来查找最相关结果的技术。

核心原理： 语义相似的物体，在向量空间中彼此靠近。

距离度量

欧几里得距离（L2距离）

任何需要测量实际物理距离的场景，如图像像素差异、GPS位置距离。在向量检索中也很常用。

公式：

L2距离 = √[ Σ (xi - yi)² ]

# Databend
L2_distance(v1, v2) = √(Σ(v1ᵢ - v2ᵢ)²)

# Python
distance = sqrt(sum((a - b) ** 2 for a, b in zip(vector1, vector2)))

含义： 两点之间的直线距离，最符合我们对"距离"的直观感受。

适用场景：

• K-means 聚类
• 物理空间位置测量
• 异常检测（离群点识别）
• 图像相似度比较（像素级）
• 物体跟踪（视频分析）

核心特点： 欧几里得距离是"绝对距离"的度量，最适合向量值有直接物理意义且各维度尺度一致的场景。

余弦相似度（COSINE_DISTANCE）

自然语言处理（词向量、文档向量相似度）、推荐系统、任何需要衡量"模式"或"趋势"是否一致的场景。

公式：

A·B = Σ (xi * yi)

# Databend
cosine_distance(v1, v2) = 1 - (Σ(v1ᵢ * v2ᵢ) / (√Σ(v1ᵢ²) * √Σ(v2ᵢ²)))

# Python
cosine_sim = dot_product(v1, v2) / (norm(v1) * norm(v2))

值域：[-1, 1]，1表示完全相同方向，-1表示完全相反

含义： 比较两个向量的方向，忽略它们的长度（模）。计算的是向量夹角的余弦值。

适用场景：

• 文本语义相似性
• 推荐系统（用户/物品向量）
• 文档聚类
• 任何忽略向量长度、只关心方向的场景

核心特点： 余弦相似度是"方向相似性"的度量，对向量长度不敏感，适合比较归一化后的特征。

内积相似度（INNER_PRODUCT）

用于衡量向量之间的对齐程度。在向量检索和机器学习中，它常被用作相似性打分函数，尤其是在向量归一化后，它等价于余弦相似度，成为语义搜索和推荐系统的核心度量之一。该算法也是 Faiss 这个库大量使用的方法。

公式：

A·B = Σ(a_i * b_i)

# Databend
inner_product(v1, v2) = Σ(v1ᵢ * v2ᵢ)

# Python
inner_product = sum(a * b for a, b in zip(vector1, vector2))

特点：

• 类型： 相似度度量
• 方向： 值越大，表示两个向量越相似（方向越一致）。反之，值越小（甚至为负），表示越不相似或方向相反。

适用场景：

• 传感器数据异常检测
• 控制系统状态评估
• 物理仿真
• 任何需要同时考虑方向和强度的场景

核心特点： 内积相似度结合了方向匹配和强度信息，在特定领域有重要应用。

近似度检索解析：三种主要度量方法的内在联系

余弦相似度与内积的关系

余弦相似度 = 内积 / (向量A长度 × 向量B长度)
内积 = 余弦相似度 × 长度A × 长度B

这意味着：

• 余弦相似度本质上是归一化后的内积
• 当向量长度固定时，内积与余弦相似度等价
• 对于长度不固定的向量，两者会给出不同的相似性排序

实战示例

向量数据库现在更多的是实现了向量类型及向量的近似度检索。下面对比一下 Python 和 Databend 实现向量使用，大家也可以自行感受一下，基于 Databend 的向量化处理会更简单一点。

Python 实现

import numpy as np

# 三个向量示例
A = np.array([1, 1])  # 长度小
B = np.array([2, 2])  # 方向相同，长度2倍
C = np.array([-1, -1])  # 方向相反

# 欧几里得距离
print("欧几里得距离:")
print(f"A-B: {np.linalg.norm(A-B):.2f}") 
print(f"A-C: {np.linalg.norm(A-C):.2f}")

# 余弦相似度
cos_sim = lambda a,b: np.dot(a,b)/(np.linalg.norm(a)*np.linalg.norm(b))
print("\n余弦相似度:")
print(f"A-B: {cos_sim(A,B):.2f}") 
print(f"A-C: {cos_sim(A,C):.2f}") 

# 内积
print("\n内积:")
print(f"A·B: {np.dot(A,B)}")
print(f"A·C: {np.dot(A,C)}")

输出：

欧几里得距离:
A-B: 1.41
A-C: 2.83

余弦相似度:
A-B: 1.00
A-C: -1.00

内积:
A·B: 4
A·C: -2

Databend SQL 实现

create or replace table t01(a vector(2), b vector(2), c vector(2));

insert into t01 values([1,1]::vector(2) ,[2,2]::vector(2) , [-1,-1]::vector(2));

select
    l2_distance(a, b), 
    l2_distance(a, c), 
    1 - cosine_distance(a, b), 
    1 - cosine_distance(a, c), 
    inner_product(a, b), 
    inner_product(a, c)
from t01;

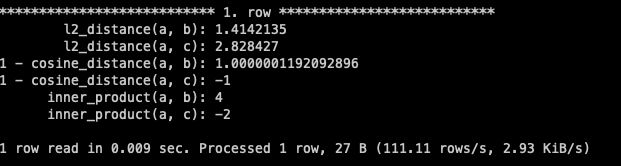
示例解析

• 欧几里得距离： A到B的距离为√2≈1.41，反映了实际的空间距离
• 余弦相似度： A与B方向相同，相似度为1；A与C方向相反，相似度为-1
• 内积： 同时考虑了方向匹配和向量长度，A·B=4，A·C=-2

总结

向量，这一起源于数学的简单概念，已经成为连接数据、算法和硬件的核心纽带。理解向量的本质不仅是掌握现代AI技术的基础，更是开启未来智能系统大门的钥匙。随着技术的不断发展，向量必将在更多领域发挥其独特价值，推动人工智能技术向更深层次迈进。

理解向量，就是理解现代AI如何"思考"——它不靠逻辑推理，而是通过在高维空间中计算距离和方向来建立认知。当我们用向量表示一切时，智能的本质就变成了在高维空间中的模式识别与关系发现。

向量技术仍在快速发展中，但它的核心地位已经确立。无论是开发者、研究者还是技术决策者，掌握向量思维都是理解当代AI系统、构建智能应用的关键能力。在这个由数字驱动的时代，向量不仅是一种技术工具，更是我们与机器智能对话的共同语言。