SCARA机械臂的运动学模型及求解

一、 DH参数介绍

DH的全称是 Denavit–Hartenberg 参数，以两位研究者（Jacques Denavit 和 Richard Hartenberg）在1955年提出该方法而命名。

它的参数一套用于描述机器人相邻连杆之间几何关系的标准化方法，其核心作用是建立机器人的运动学模型，将关节空间（每个关节的转动/移动量）映射到末端执行器的笛卡尔空间位置和姿态。

可以把DH参数看作是描述两个“邻居”连杆关系的“四要素身份证”，对于由一系列连杆和关节组成的串联机器人，每两个相邻连杆之间都可以用这四个参数来唯一定义它们的相对位置和方向，四个参数如下：

关键点：

• a和 α 描述了连杆本身的固有几何特征（长度和弯曲程度），对于平移关节和旋转关节来说，通常是常量。
• d和 θ 描述了相邻连杆的相对位置，其中一个是变量，取决于关节类型：
  • 如果关节i是旋转关节，则 θᵢ是变量，dᵢ是常量。
  • 如果关节i是平移关节，则 dᵢ是变量，θᵢ是常量。

二、 DH建模流程

DH参数的主要用途是构建正运动学模型，这是机器人控制和编程的基础，工作流程如下：

1. 建模：为机器人的每个连杆建立坐标系，并确定相邻坐标系之间的4个DH参数。
2. 计算变换矩阵：利用这四个参数，可以计算出一个标准的 4x4 齐次变换矩阵，它完整描述了从“连杆i-1的坐标系”到“连杆i的坐标系”的变换（包含旋转和平移）。变换矩阵公式是固定的，由 a, α, d, θ四个参数计算得出。
3. 串联变换：从机器人的基座（连杆0）到末端执行器（连杆n），将所有相邻连杆的变换矩阵连乘起来。T₀ⁿ = T₀¹ * T₁² * ... * Tⁿ⁻¹ⁿ
4. 得到正运动学方程：最终结果 T₀ⁿ是一个矩阵，告诉你末端执行器相对于机器人基座的位置 (x, y, z) 和姿态（旋转矩阵），这个矩阵是各个关节变量（θᵢ或 dᵢ）的函数。

想象一个简单的2自由度平面机械臂（两个旋转关节）：

• 基座关节：连接地面和第一个连杆
• 肘关节：连接第一个和第二个连杆
• 末端：在第二个连杆的末端

DH建模过程如下：

1. 在基座、肘关节、末端分别建立坐标系（Z轴沿关节旋转轴，X轴沿连杆垂直方向）。
2. 确定两组DH参数（a1, α1, d1, θ1和 a2, α2, d2, θ2）。
   • a1, a2就是两个连杆的长度。
   • d和 α通常为0（因为在一个平面内）。
   • θ1, θ2就是两个关节的旋转角度（变量）。
3. 计算出变换矩阵 T₀¹(θ1)和 T₁²(θ2)。
4. 连乘得到 T₀² = T₀¹ * T₁²。这个矩阵的右上角3x1向量 [x; y; z]就是末端位置，它等于：
   • x = a1*cos(θ1) + a2*cos(θ1+θ2)
   • y = a1*sin(θ1) + a2*sin(θ1+θ2)
   • z = 0

这就完成了平面机械臂正运动学方程建模

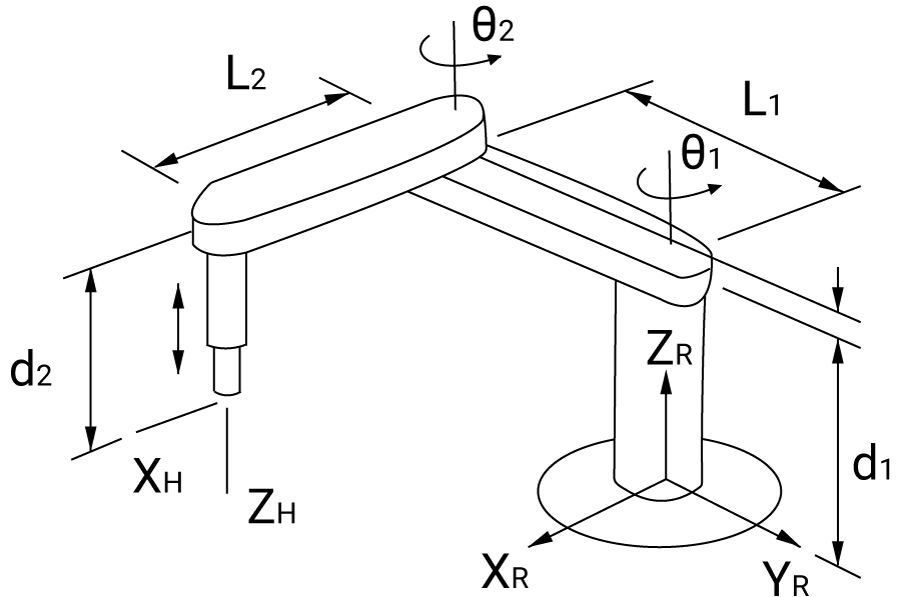
三、SCARA运动学模型

3.1 标准4自由度SCARA的DH参数表：

3.2 变换矩阵

T₀⁴ = T₀¹(θ₁) · T₁²(θ₂) · T₂³(d₃) · T₃⁴(θ₄)

T₀¹ = [cosθ₁  -sinθ₁   0   a₁cosθ₁]
       [sinθ₁   cosθ₁   0   a₁sinθ₁]
       [0       0       1      d₁  ]
       [0       0       0      1   ]
T₁² = [cosθ₂   sinθ₂   0   a₂cosθ₂]
       [sinθ₂  -cosθ₂   0   a₂sinθ₂]
       [0       0      -1      0   ]
       [0       0       0      1   ]
T₂³ = [1       0       0       0  ]
       [0       1       0       0  ]
       [0       0       1       d₃ ]
       [0       0       0       1  ]
T₃⁴ = [cosθ₄  -sinθ₄   0       0  ]
       [sinθ₄   cosθ₄   0       0  ]
       [0       0       1       d₄ ]
       [0       0       0       1  ]

3.3 运动学求解末端姿态

末端位置
x = a₁cosθ₁ + a₂cos(θ₁+θ₂)
y = a₁sinθ₁ + a₂sin(θ₁+θ₂)
z = d₁ - d₃  （注意：d₃为正值时末端下降）
末端角度
φ = θ₁ + θ₂ + θ₄

3.4 逆运动学求解

给定末端位姿(x, y, z, φ)，求关节变量：

a. 求θ₂：

c₂ = (x² + y² - a₁² - a₂²) / (2a₁a₂)
有两种解：
肘部向上：θ₂ = atan2(√(1-c₂²), c₂)
肘部向下：θ₂ = atan2(-√(1-c₂²), c₂)

b. 求θ₁：

θ₁ = atan2(y, x) - atan2(a₂s₂, a₁ + a₂c₂)
其中 s₂ = sinθ₂, c₂ = cosθ₂

c. 求d₃：

d₃ = d₁ - z

d. 求θ₄：

θ₄ = φ - (θ₁ + θ₂)