问如何旋转和缩放一个同形
EN

Stack Overflow用户

提问于 2012-05-23 05:46:13

回答 2查看 3K关注 0票数 5

我需要帮助

我正在从服务器接收到一个同形，所以我想将此同形规范化到我的应用程序的坐标系中，当我试图用坐标表示一个对象时，服务器应用程序生成接下来的4个点：

收到96.629539,217.31934；97.289948,167.21941；145.69249,168.28044；145.69638,219.84604

我的应用程序生成了接下来的4分：

本地126.0098，55.600437；262.39163，53.98035；259.41382,195.34763；121.48138,184.95235

I你用图形表示这个点，R(接收)，P(本地)

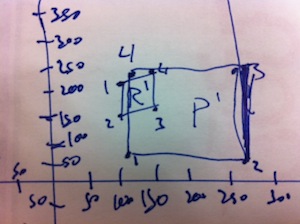
看起来所生成的正方形是旋转和缩放的，所以我想知道是否有任何方法将这种旋转--一个比例--应用于服务器单形，以便能够拥有与我的应用程序相同的同形。

谢谢，我需要更多的信息，请问我。

非常感谢您的快速回答，在最后我使用其他近似，就像从服务器获得点和使用findhomography得到反单形一样简单。

homography=findHomography(srcPoints，dstPoints，match_mask，RANSAC，10)；

谢谢！

algorithm

math

opencv

augmented-reality

语音识别特惠，低至14.9元！

提供业界非常具有性价比的语音识别服务，超高识别准确率，适用多场景

回答 2

Stack Overflow用户

发布于 2012-05-23 07:30:55

我想我想明白了。下面是一个更准确的情节，你的两个同音。其中蓝色是接收到的同形，红色是本地的同形。

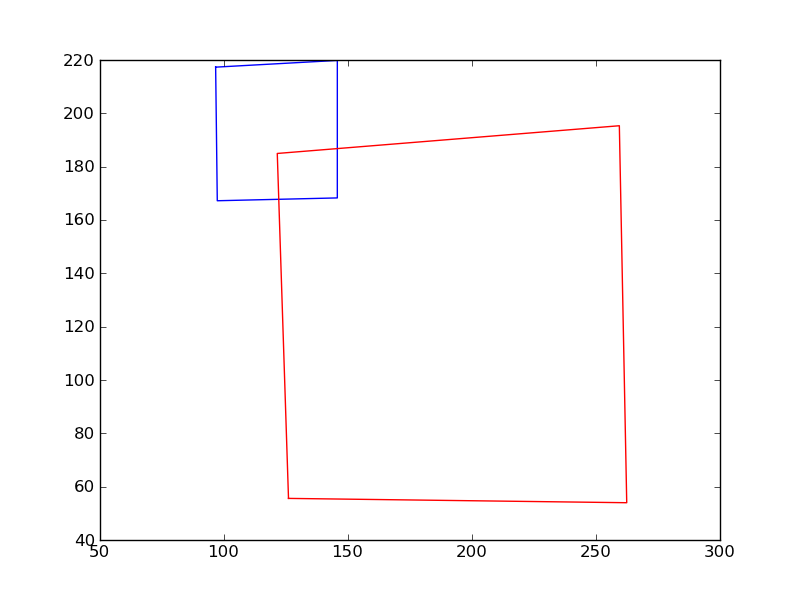
您可以使用OpenCV函数getAffineTransform来计算与3对点对相关的仿射变换(我必须重新组织点对，因为它们的顺序不对)。我在numpy中运行了以下代码：

r = array([[97.289948, 167.21941], [96.629539, 217.31934], [145.69638, 219.84604]], np.float32)
l = array([[126.0098, 55.600437], [121.48138, 184.95235], [259.41382, 195.34763]], np.float32)
A = cv2.getAffineTransform(r, l)

这给了我们以下仿射关系：

array([[  2.81385763e+00,  -5.32961421e-02,  -1.38838108e+02],
       [  7.88519054e-02,   2.58291747e+00,  -3.83984986e+02]])

我将其应用到r中，看看是否可以让l确保它像这样工作：

# split affine warp into rotation, scale, and/or shear + translation matrix
T = mat(A[:, 2]).T
matrix([[-138.83810801],
        [-383.98498637]])

A = mat(A[:, 0:2])
matrix([[ 2.81385763, -0.05329614],
        [ 0.07885191,  2.58291747]])

# apply warp to r to get l
r = mat(r).T
A*r + T
# gives
matrix([[ 126.00980377,  121.48137665,  259.41381836],
        [  55.60043716,  184.9523468 ,  195.34762573]])
# which equals
l = mat(l).T
matrix([[ 126.00980377,  121.48137665,  259.41381836],
        [  55.60043716,  184.9523468 ,  195.34762573]], dtype=float32)

同样值得注意的是，您可以使用Markus Jarderot函数getPerspectiveTransform生成透视图转换，如OpenCV所示。

希望这能帮上忙！

票数 4

Stack Overflow用户

发布于 2012-05-23 08:28:50

如果将点和转换插入到Maple中，则可以很快得到结果。

> with(LinearAlgebra);

> # The server coordinates
  pa := [[96.629539, 217.31934], [97.289948, 167.21941], [145.69249, 168.28044],
         [145.69638, 219.84604]]:

> # The local coordiantes
  pb := [[126.0098, 55.600437], [262.39163, 53.98035], [259.41382, 195.34763],
         [121.48138, 184.95235]]:

> # The placeholder variables for the transformation (last one is '1', because it
  # is scale-invariant)
  T := [seq]([seq](`if`(i = 3 and j = 3, 1, t[i, j]), j = 1 .. 3), i = 1 .. 3):
  V := convert(map(op, T)[1 .. -2], set):

> # Transformation function (Matrix multiplication + divide with 3rd coordinate)
  trans := (p, T) -> [
      (T[1, 1]*p[1]+T[1, 2]*p[2]+T[1, 3])/(T[3, 1]*p[1]+T[3, 2]*p[2]+T[3, 3]),
      (T[2, 1]*p[1]+T[2, 2]*p[2]+T[2, 3])/(T[3, 1]*p[1]+T[3, 2]*p[2]+T[3, 3])
  ]:

> # Transform pa, and construct the equation system
  pat := map(trans, pa, T):
  eqs := {op}(zip((p1, p2) -> op(zip(`=`, p1, p2)), pat, pb)):

> # Solve for the transform variables
  sol := solve(eqs, V):

> # Populate the transform
  eval(T, sol);

输出：

[[  .1076044020,   -3.957029830,    1074.517140  ],
 [ 4.795375318,      .3064507355,   -430.7044862 ],
 [ 0.3875626264e-3, 0.3441632491e-2,   1         ]]

若要使用此方法，请将其与服务器点相乘为T * <x, y, 1>。

void ServerToLocal(double serverX, double serverY, double *localX, double *localY)
{
    double w;
    w = 0.3875626264e-3 * serverX + 0.3441632491e-2 * serverY + 1.0;
    *localX = (.1076044020 * serverX - 3.957029830 * serverY + 1074.517140) / w;
    *localY = (4.795375318 * serverX + .3064507355 * serverY - 430.7044862) / w;
}