数据结构--树状数组

Michael阿明

发布于 2020-07-13 08:20:30

1.9K00

代码可运行

文章被收录于专栏：Michael阿明学习之路Michael阿明学习之路

运行总次数：0

代码可运行

1. 树状数组

类似数据结构：线段树（Segment Tree）

树状数组跟线段树的区别：

树状数组能做的事情，线段树都能做！（线段树功能更牛）
树状数组代码简单，实现起来比线段树容易（树状数组代码更简单）

树状数组的查询和修改复杂度都为

log (n)

$\log(n)$

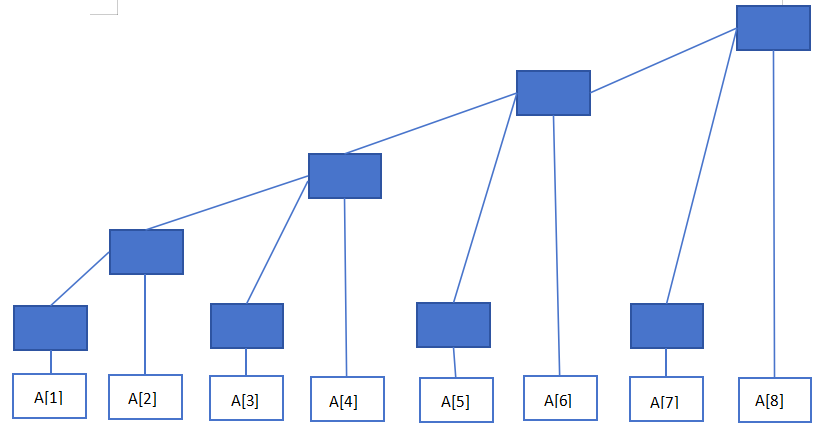
原数组为 A
树状数组为 C（注意下标从1开始！！！）

C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

对 C8 （8的2进制为1000，后面有3个0，所以他管着3个数C4、C6、C7，还有自己A8）
奇数末尾没有0，所以奇数位只有自己
那怎么计算一个数管着几个数呢？

2. 单点修改

树状数组的核心函数lowbit(int m)：作用是求出 m 的二进制表示的末尾1的位置，对于要查询 m 的前缀和，m = m - lowbit(m) 代表不断对二进制末尾1进行-1操作，不断执行直到 m == 0 结束，就能得到前缀和由哪几个Cm构成

int lowbit(int m){
    return m & (-m);//(获取最后一个1的10进制值)
}
int getsum(int i){    //求A[1],A[2],...A[i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

对8（1000）来算下：补充：负数的二进制是正数取反末尾+1

8 & (-8) = 1000 & (.111..1000) = 1000 = 8....8-8=0,sum=C8=A[1]+..A[8]
-------------
6 & (-6) =  0110 & (1010) = 10 = 2 .... 6-2=4,sum=C6
4 & (-4) = 0100 & (1100) = 100 = 4.....4-4=0,sum+=C4=C6+C4=A[1]+...A[6]
-------------
奇数上面操作结果均为 1

#include <bits/stdc++.h>
using namespace std;

const int N = 8;
int a[N+1]={0,1,2,3,4,5,6,7,8}, c[N+1] = {0}; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}
//修改操作就是getsum的逆过程
void update(int i, int delta){    //在i位置加上delta
    while(i <= N){
        c[i] += delta;
        i += lowbit(i);
    }
}

int getsum(int i){    //求A[1],A[2],...A[i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    for(int i = 1; i <= N; ++i)
        update(i,a[i]);//读取原数据，插入树状数组
    cout << getsum(3) << endl;//获取前3个数的和
    cout << getsum(8) << endl;
    update(3,2);
    cout << getsum(3) << endl;
    cout << getsum(8) << endl;
    cout << getsum(4)-getsum(2) << endl;//获取A[3],A[4]的区间和
    return 0;
}

结果：

3. 区间修改

将原数组的差值A[i]-A[i-1],(A[0]=0)存入树状数组

A[i] = 1 2 3 5 6 9
D[i] = 1 1 1 2 1 3 (差值)

把[2,5]区间内值加上2，则变成了

A[i] = 1 4 5 7 8 9
D[i] = 1 3 1 2 1 1

发现只有L和R+1处的值需要修改（左边+，右边-），降低了时间复杂度所以，update修改的时候，只需要修改两个端点（因为中间的差值不变）那么上面的 getsum(i) 的结果就是原数组的A[i]，很好证明，高中数学（把D[i] 加一下也能发现）

那在上面基础上，我们获取区间的和怎么办？先来推导一下：

A [i] = D [i] + D [i - 1] + . . . + D [1] A [i - 1] = D [i - 1] + D [i - 2] + . . . + D [1] . . . A [2] = D [2] + D [1] A [1] = D [1]

$A[i] = D[i] + D[i-1]+...+D[1]\\ A[i-1] = D[i-1] + D[i-2]+...+D[1]\\ ... \\ A[2] = D[2] +D[1]\\ A[1] = D[1]$

左右都加起来：

i \sum x = 1 A [x] = i * D [1] + (i - 1) * D [2] + . . . + 1 * D [i] = i * i \sum x = 1 D [x] - i \sum x = 1 (D [x] * (x - 1))

$\sum\limits_{x=1}^i A[x] = i*D[1] + (i-1)*D[2] +... +1*D[i] =i*\sum\limits_{x = 1}^i D[x] - \sum\limits_{x = 1}^i ( D[x]*(x-1))$

看见最后两项，就明白了吧，再增加一个树状数组存入

D [x] * (x - 1)

$D[x]*(x-1)$

#include <bits/stdc++.h>
using namespace std;

const int N = 8;
int a[N+1]={0,1,2,3,4,5,6,7,8}, c[N+1] = {0}; //对应原数组和树状数组
int sum1[N+1] = {0}, sum2[N+1] = {0};//对应D[i] , D[i]*(i-1)

int lowbit(int x){
    return x&(-x);
}
//------区间修改-------
void update1(int i, int delta){    //在i位置加上delta
    int x = i;//系数不能变，先存起来
    while(i <= N){
        sum1[i] += delta;
        sum2[i] += delta*(x-1);
        i += lowbit(i);
    }
}
void update_range(int l, int r, int delta)    //给区间加上delta
{
    update1(l, delta);//只需修改L，R+1，左+，右-
    update1(r+1, -delta);
}

int query_p(int i){	//A[1],A[2]...A[i]的和
    int res = 0, x = i;//系数不能变，先存起来
    while(i > 0){
        res += x*sum1[i] - sum2[i];
        i -= lowbit(i);
    }
    return res;
}
int query_range(int l, int r)	//区间[l,r]的和
{
    return query_p(r)-query_p(l-1);
}
int main(){
    cout << "区间修改，单点查询" << endl;
    for(int i = 1; i <= N; ++i)
        update1(i,a[i]-a[i-1]);//读取原数据差值，插入树状数组
    cout << query_p(3) << endl;//获取前3个数的和
    cout << query_p(8) << endl;
    update_range(3,3,2);//修改区间【3，3】，都加上2
    cout << query_p(3) << endl;
    cout << query_p(8) << endl;
    cout << query_range(3,4) << endl;//获取A[3],A[4]的区间和
    return 0;
}

运行结果

相关题目：程序员面试金典 - 面试题 10.10. 数字流的秩（map/树状数组） LeetCode 307. 区域和检索 - 数组可修改（树状数组）

4. 完整代码

/**
 * @Description: 树状数组
 * @Author: michael ming
 * @Date: 2020/4/1 23:38
 * @Modified by: 
 * @Website: https://michael.blog.csdn.net/
 */

#include <bits/stdc++.h>
using namespace std;

const int N = 8;
int a[N+1]={0,1,2,3,4,5,6,7,8}, c[N+1] = {0}; //对应原数组和树状数组
int sum1[N+1] = {0}, sum2[N+1] = {0}; //对应D[i] , D[i]*(i-1)
int lowbit(int x){
    return x&(-x);
}
//-------单点修改----------
void update(int i, int delta){    //在i位置加上delta（单点）
    while(i <= N){
        c[i] += delta;
        i += lowbit(i);
    }
}

int query(int i){    //求A[1],A[2],...A[i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

//------区间修改-------
void update1(int i, int delta){    //在i位置加上delta
    int x = i;//系数不能变，先存起来
    while(i <= N){
        sum1[i] += delta;
        sum2[i] += delta*(x-1);
        i += lowbit(i);
    }
}
void update_range(int l, int r, int delta)    //给区间加上delta
{
    update1(l, delta);//只需修改L，R+1，左+，右-
    update1(r+1, -delta);
}

int query_p(int i){
    int res = 0, x = i;//系数不能变，先存起来
    while(i > 0){
        res += x*sum1[i] - sum2[i];
        i -= lowbit(i);
    }
    return res;
}
int query_range(int l, int r)//区间[l,r]的和
{
    return query_p(r)-query_p(l-1);
}
int main(){
    //单点修改
    cout << "单点修改，单点查询" << endl;
    for(int i = 1; i <= N; ++i)
        update(i,a[i]);//读取原数据，插入树状数组
    cout << query(3) << endl;//获取前3个数的和
    cout << query(8) << endl;
    update(3,2);
    cout << query(3) << endl;
    cout << query(8) << endl;
    cout << query(4)-query(2) << endl;//获取A[3],A[4]的区间和
    cout << "区间修改，单点查询" << endl;
    for(int i = 1; i <= N; ++i)
        update1(i,a[i]-a[i-1]);//读取原数据差值，插入树状数组
    cout << query_p(3) << endl;//获取前3个数的和
    cout << query_p(8) << endl;
    update_range(3,3,2);//修改区间【3，3】，都加上2
    cout << query_p(3) << endl;
    cout << query_p(8) << endl;
    cout << query_range(3,4) << endl;//获取A[3],A[4]的区间和
    return 0;
}