【概率论与数理统计(研究生课程)】知识点总结9(回归分析)
【概率论与数理统计(研究生课程)】知识点总结9(回归分析)

Marigold
发布于 2023-08-24 10:02:55
发布于 2023-08-24 10:02:55
一元线性回归模型
$$ \begin{aligned} &y=\beta_0+\beta_1x+\epsilon,\quad \epsilon \sim N(\mu, \sigma^2) \ &E(\epsilon)=0,D(\epsilon)=\sigma^2>0 \Longrightarrow E(y)=\beta_0+\beta_1x \end{aligned} $$
回归方程:\hat{y}=\hat{\beta_0}+\hat{\beta_1}x
\begin{aligned} y_i-E(y_i)&=y_i-(\beta_0+\beta_1x_i) \ Q(\beta_1, \beta_2)&=\sum\limits_{i=1}^{n}(y_i-E(y_i))^2 \ &=\sum\limits_{i=1}^{n}(y_i-\beta_0-\beta_1x_i)^2 \ \text{make }\quad\frac{\partial{Q(\beta_0,\beta_1)}}{\partial{\beta_0}}&=-2\sum\limits_{i=1}^{n}(y_i-\beta_0-\beta_1x_i)=0 \ \text{make }\quad\frac{\partial{Q(\beta_0,\beta_1)}}{\partial{\beta_1}}&=-2\sum\limits_{i=1}^{n}x_i(y_i-\beta_0-\beta_1x_i)=0 \ \end{aligned}
\end{aligned}
\begin{aligned} &\hat{\beta_1}=\frac{L_{xy}}{L_{xx}} \ &\hat{\beta_0}=\bar{y}-\hat{\beta_1}\bar{x} \ &L_{xx}=\sum\limits_{i=1}^{n}(x_i-\bar{x})^2=\sum\limits_{i=1}^{n}x_i^2-n\bar{x}^2=\sum\limits_{i=1}^{n}x_i^2-\frac{1}{n}(\sum\limits_{i=1}^{n}x_i)^2 \ &L_{yy}=\sum\limits_{i=1}^{n}(y_i-\bar{y})^2=\sum\limits_{i=1}^{n}y_i^2-n\bar{y}^2=\sum\limits_{i=1}^{n}y_i^2-\frac{1}{n}(\sum\limits_{i=1}^{n}y_i)^2 \ &L_{xy}=\sum\limits_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})=\sum\limits_{i=1}^{n}x_iy_i-n\bar{x}\bar{y}=\sum\limits_{i=1}^{n}x_iy_i-\frac{1}{n}\sum\limits_{i=1}^{n}x_i \sum\limits_{i=1}^{n}y_i \end{aligned}
如果题目中给了\sum形式的数据, L_{xx},L_{yy},L_{xy}一般用上述公式最右边的方式来求。
残差/剩余平方和
定理:\frac{Q_e}{\sigma^2}\sim\chi^2(n-2) \begin{aligned} &E(\frac{Q_e}{\sigma^2})=n-2 \ \Longrightarrow \quad &E(\frac{Q_e}{n-2})=\sigma^2 \ \Longrightarrow \quad &\hat{\sigma^2}=\frac{Q_e}{n-2} \end{aligned} 的无偏估计为\frac{Q_e}{n-2}
最小二乘估计量的性质
\beta_0,\beta_1的最小二乘估计量都是无偏的:E(\hat{\beta_0})=\beta_0,\quad E(\hat{\beta_1})=\beta_1
\hat{\beta_0}\sim N(\beta_0, (\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}})\sigma^2)
\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}})
Cov(\hat{\beta_0},\hat{\beta_1})=-\frac{\bar{x}}{L_{xx}}\sigma^2
\hat{y_0}\sim N(\beta_0+\beta_1x_0, (\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}})\sigma^2)
回归方程显著性检验(t、F、r)
- 提出原假设和备择假设(回归方程是否显著,反映在斜率是否为0):
- \begin{aligned} &\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}}) \ \Longrightarrow \quad &\frac{\hat{\beta_1}-\beta_1}{\sqrt{\frac{\sigma^2}{L_{xx}}}}\sim N(0,1) \ \xrightarrow{H_0} \quad &\frac{\hat{\beta_1}\sqrt{L_{xx}}}{\sigma}\sim N(0,1) \end{aligned} 若使用
- 拒绝域 t检验拒绝域:|T|=|\frac{\hat{\beta_1}\sqrt{L_{xx}}}{\hat{\sigma}}|\ge t_{\frac{\alpha}{2}}(n-2) F检验拒绝域:F\ge F_\alpha(1,n-2)
- 确定t_{\frac{\alpha}{2}(n-2)}\quad or \quad F_{\alpha}(1,n-2)
- 计算|T|\quad or\quad F
- 判断结果
回归系数的区间估计
$$ \begin{aligned} &\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}}) \
\Longrightarrow \quad &\frac{\hat{\beta_1}-\beta_1}{\sqrt{\frac{\sigma^2}{L_{xx}}}}\sim N(0,1) \
\Longrightarrow \quad &\frac{(\hat{\beta_1}-\beta_1)\sqrt{L_{xx}}}{\sigma}\sim N(0,1) \
T=\frac{\frac{(\hat{\beta_1}-\beta_1)\sqrt{L_{xx}}}{\sigma}}{\sqrt{\frac{Q_e}{\sigma^2}/(n-2)}}&\xrightarrow{\hat{\sigma^2}=\frac{Q_e}{n-2}}\frac{(\hat{\beta_1}-\beta_1)\sqrt{L_{xx}}}{\hat\sigma} \sim t(n-2) \end{aligned} $$
则\beta_1置信水平为1-\alpha的置信区间为:(\hat{\beta_1}\pm \frac{\hat{\sigma}}{\sqrt{L_{xx}}}t_{\frac{\alpha}{2}}(n-2))
估计
设回归方程为\hat{y}=\hat{\beta_0}+\hat{\beta_1}x,对任意给定的x=x_0,y_0的均值E(y_0)=\beta_0+\beta_1 x_0,E(y_0)的无偏估计为\hat{y_0}=\hat{\beta_0}+\hat{\beta_1}x_0
\hat{\beta_0}\sim N(\beta_0, (\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}})\sigma^2)
\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}})
Cov(\hat{\beta_0},\hat{\beta_1})=-\frac{\bar{x}}{L_{xx}}\sigma^2
D(\hat{y_0})=D(\hat{\beta_0})+D(\hat{\beta_1}x_0)+2Cov(\hat{\beta_0},\hat{\beta_1}x_0)=(\frac{1}{n}+\frac{(\bar{x}-x_0)^2}{L_{xx}})\sigma^2
的置信区间为:
区间预测
$$ \begin{aligned} y_0-\hat{y_0}\sim N(0,[1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}]\sigma^2) \ U=\frac{y_0-\hat{y_0}}{\sigma\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}}}\sim N(0,1) \ T=\frac{y_0-\hat{y_0}}{\hat\sigma\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}}}\sim t(n-2) \end{aligned} $$
的区间为
可线性化的一元非线性回归
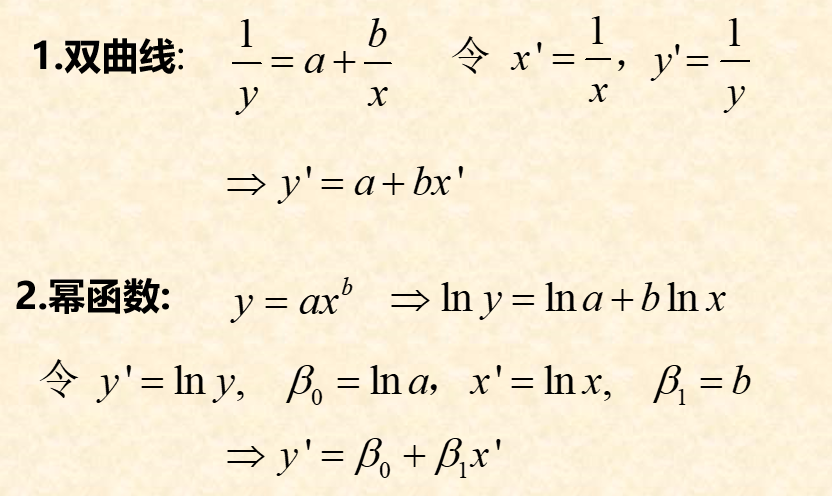
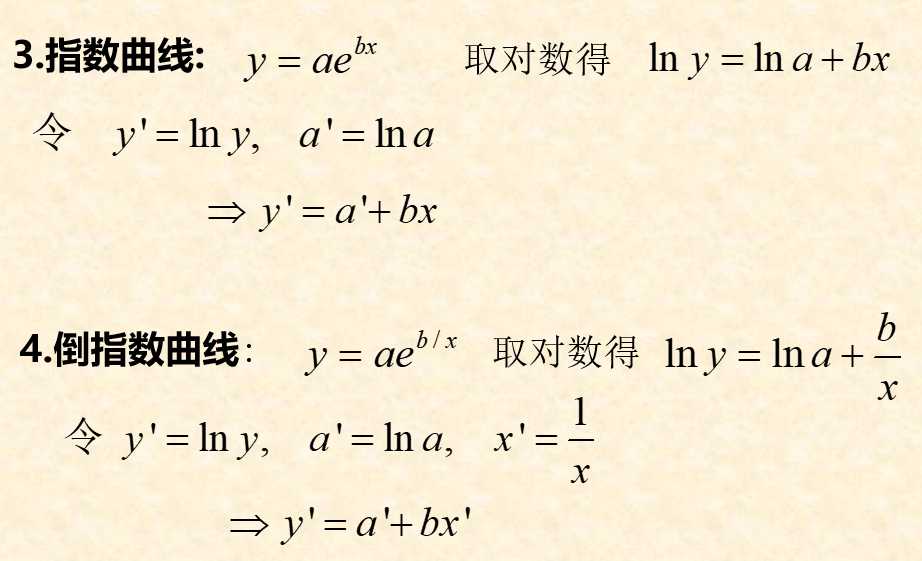
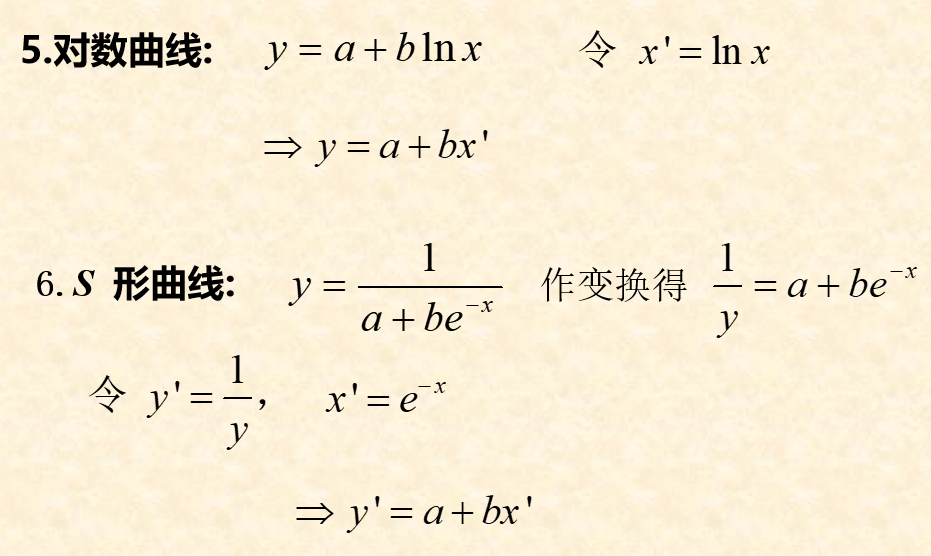
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2022/11/03 ,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

