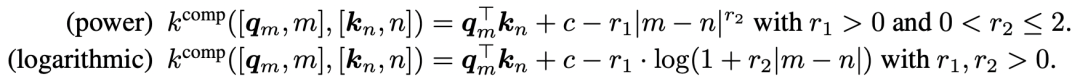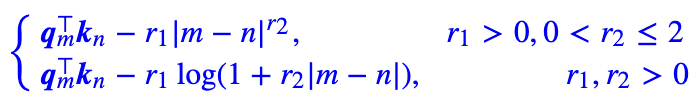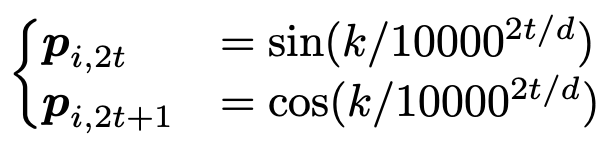大家好,这里是 NewBeeNLP。
现如今很多大模型都开始支持超过4096长度的推理,例如GPT-4支持超过30k,ChatGLM2-6B也支持最长为32K的文本。但是由于显存资源的限制,这些大模型在真正在训练过程中不一定要训练这么长的文本,通常在预训练时只会设计到4k左右。
因此 如何确保在模型推理阶段可以支持远远超过预训练时的长度 ,是目前大模型的核心问题之一,我们将这一问题归为 大模型的外推性 。
大模型的外推性目前主要在这两个方面考虑,也是提升最有效的两个角度:
本文从这两方面进行深度探讨大模型的位置编码和外推性问题。
一、位置编码基础介绍 对于一个token
w_i ,其表征向量记作
x_i ,对于一个句子
w=\left\{w_1, \cdots\right\} 则表示为
x 。那么可以通过一个映射函数将这个句子中的token表征为
\mathbf{q}_m, \mathbf{k}_n , \mathbf{v}_n :
\begin{aligned}
\boldsymbol{q}_m & =f_q\left(\boldsymbol{x}_m, m\right) \\
\boldsymbol{k}_n & =f_k\left(\boldsymbol{x}_n, n\right) \\
\boldsymbol{v}_n & =f_v\left(\boldsymbol{x}_n, n\right)
\end{aligned}
其中
m 和
n 表示第
m 和第
n 个token。
1.1 绝对位置编码 在Transformer中,采用正余弦函数来表示绝对位置,公式如下:
\begin{cases}\boldsymbol{p}_{i, 2 t} & =\sin \left(k / 10000^{2 t / d}\right) \\ \boldsymbol{p}_{i, 2 t+1} & =\cos \left(k / 10000^{2 t / d}\right)\end{cases}
这种编码方式又叫做 Sinusoidal编码 。直觉上看,第
i 个位置的表征向量维度是
d ,这个向量的奇数位置元素使用余弦值,偶数位置元素使用正弦值。
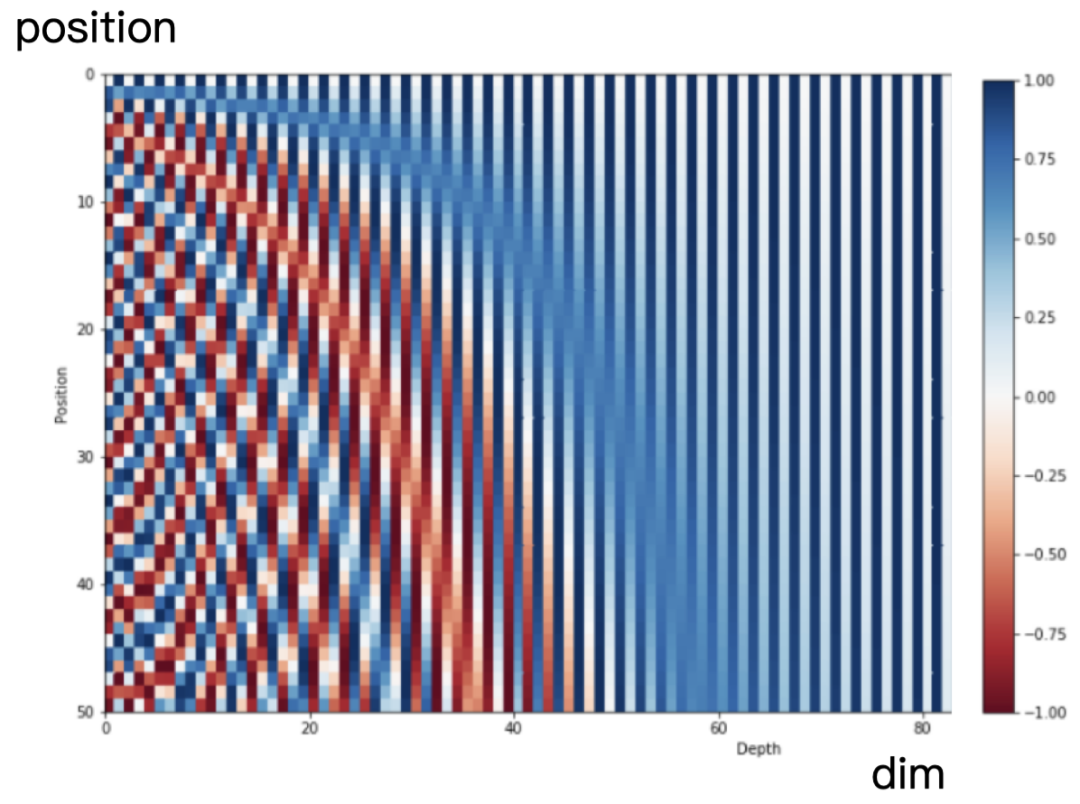
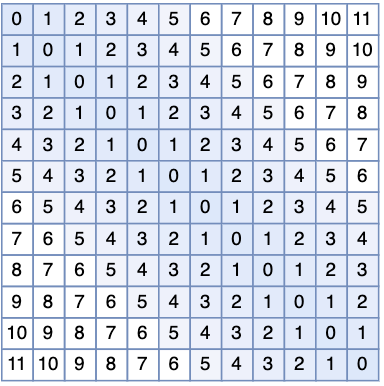
可视化图如下所示:
相邻的位置编码向量很相似,较远的位置编码向量差异很大,说明基于正余弦函数的绝对位置可以表征位置的相关性; 不需要显式地学习位置,提高效率。 最后
f 映射函数可以定义如下所示。即输入表征为token的表征和其对应的绝对位置表征。
f_{t: t \in\{q, k, v\}}\left(\boldsymbol{x}_i, i\right):=\boldsymbol{W}_{t: t \in\{q, k, v\}}\left(\boldsymbol{x}_i+\boldsymbol{p}_i\right),
该表征通常是直接将位置表征与Word表征直接相加。
1.2 相对位置编码 (1)显式的相对位置
对于第
m 和第
n 个位置的token,其相对位置可以表示为
r=\operatorname{clip}\left(m-n, r_{\min }, r_{\max }\right) ,即两个token之间的相对距离,且由最大最小值做约束(相对位置不能超过最大值或小于最小值)。
因此,相比于绝对位置,相对位置只需要有
r_{\max }-r_{\min }+1 表征向量即可,即在计算两个token之间的attention值时,只需要在attention计算过程中注入这两个位置对应的相对位置
r 对应的相对位置表征向量即可:
\begin{array}{r}
f_q\left(\boldsymbol{x}_m\right):=\boldsymbol{W}_q \boldsymbol{x}_m \\
f_k\left(\boldsymbol{x}_n, n\right):=\boldsymbol{W}_k\left(\boldsymbol{x}_n+\tilde{\boldsymbol{p}}_r^k\right) \\
f_v\left(\boldsymbol{x}_n, n\right):=\boldsymbol{W}_v\left(\boldsymbol{x}_n+\tilde{\boldsymbol{p}}_r^v\right)
\end{array}
这样一来,只需要有限个位置编码,就可以表达出任意长度的相对位置(因为进行了截断),不管是选择可训练式的还是三角函数式的,都可以达到处理任意长度文本的需求。
该表征通常是直接将位置表征与Word表征直接相加。
参考论文:《Self-Attention with Relative Position Representations》
(2)Transformer-XL(XLNet)
将第
m 和第
n 个位置的QK计算进行了分解。引入了一些可学习的参数:
\boldsymbol{q}_m^{\boldsymbol{\top}} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{p}_n+\boldsymbol{p}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{p}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{p}_n,
其中
p_m 表示待学习的第
m 个token的相对位置向量,
p_n 表示待学习的第
n 个token的相对位置向量。通过分解让相对位置注入在attention的计算过程中。
该表征通常是在Attention计算过程中融入绝对位置。
(3)Transformer-XL的改进
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\boldsymbol{\top}} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\boldsymbol{\top}} \widetilde{\boldsymbol{W}}_k \tilde{\boldsymbol{p}}_{m-n}+\mathbf{u}^{\boldsymbol{\top}} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\mathbf{v}^{\top} \boldsymbol{W}_q^{\top} \widetilde{\boldsymbol{W}}_k \tilde{\boldsymbol{p}}_{m-n}
第二和第四项使用相对位置表征
\tilde{\mathbf{p}}_{m-n} 来替换绝对位置表征。同时加入新的可训练参数
u 和
v 。
该表征方法在T5模型中被首次使用,参考论文:《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》
该表征通常是在Attention计算过程中融入相对位置。
(4)可训练偏置项
Transformer-XL中的位置表征是将QK分解为4项,而后面3个够项都有跟位置有关的参数,可以直接将后面的3项之和抽象为一个偏置:
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+b_{i, j}
进一步改造还可以得到:
\boldsymbol{q}_m^{\boldsymbol{\top}} \boldsymbol{k}_n=\boldsymbol{x}_m^{\boldsymbol{\top}} \boldsymbol{W}_q^{\boldsymbol{\top}} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{p}_m^{\boldsymbol{\top}} \mathbf{U}_q^{\top} \mathbf{U}_k \boldsymbol{p}_n+b_{i, j}
以及:
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \tilde{\boldsymbol{p}}_{m-n}+\tilde{\boldsymbol{p}}_{m-n}^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n
这三种方法均是对Transformer-XL的表征形式进行改进。
二、RoPE旋转位置编码 RoPE(Rotary Position Embedding)的出发点就是“ 通过绝对位置编码的方式实现相对位置编码 ”,或者可以说是实现 相对位置编码和绝对位置编码的结合 。
这样做既有理论上的优雅之处,也有实践上的实用之处,比如它可以拓展到线性Attention中就是主要因为这一点。
2.1 复数的引入 假设
q_m 和
k_n 是对应位置的二维行向量(即每个位置都有两个向量来表征位置),因此这个二维向量可以用复数来代替(包括实部和虚部),因此他们的内积可以作为其对应的Attention值。
内积的计算可以由两个复数实现:
\left\langle\mathbf{q}_m, \mathbf{k}_n\right\rangle=R E\left[\mathbf{q}_m \mathbf{k}_n^*\right] ,其中
∗ 表示共轭复数,
RE[] 表示取复数中的实部。
两个二维向量的内积,等于把它们当复数看时,一个复数与另一个复数的共轭的乘积的实部。
因此当分别对
q_m 和
k_n 融入绝对位置时,即得到:
\left\langle\boldsymbol{q}_m e^{\mathrm{i} m \theta}, \boldsymbol{k}_n e^{\mathrm{i} n \theta}\right\rangle=\operatorname{Re}\left[\left(\boldsymbol{q}_m e^{\mathrm{i} m \theta}\right)\left(\boldsymbol{k}_n e^{\mathrm{i} n \theta}\right)^*\right]=\operatorname{Re}\left[\boldsymbol{q}_m \boldsymbol{k}_n^* e^{\mathrm{i}(m-n) \theta}\right]
RoPE求解过程推导了如何确定获得每个位置编码是
\mathbf{q}_m e^{i m \theta} 。
可以发现,当乘以绝对位置
e^{imθ} 和
e^{inθ} 时,等价于复数运算中乘以
e^{i(m−n)θ} ,即相当于在复数空间中是相对位置
m−n ,这样就巧妙地通过复数运算的形式将绝对位置转换为相对位置。
复数乘法的几何意义是向量的旋转,假设
\mathcal{f}_{q, k}(\mathbf{x}, m) 表示向量
x 在
m 位置的位置编码,则有:
\begin{aligned}
f_q\left(\boldsymbol{x}_m, m\right) & =\left(\boldsymbol{W}_q \boldsymbol{x}_m\right) e^{i m \theta} \\
f_k\left(\boldsymbol{x}_n, n\right) & =\left(\boldsymbol{W}_k \boldsymbol{x}_n\right) e^{i n \theta}
\end{aligned}
其中
\mathbf{q}=\mathbf{W}_q \mathbf{x}_m, \mathbf{k}=\mathbf{W}_k \mathbf{x}_n 等价于
f_{\{q, k\}}\left(\boldsymbol{x}_m, m\right)=\left(\begin{array}{cc}
\cos m \theta & -\sin m \theta \\
\sin m \theta & \cos m \theta
\end{array}\right)\left(\begin{array}{cc}
W_{\{q, k\}}^{(11)} & W_{\{q, k\}}^{(12)} \\
W_{\{q, k\}}^{(21)} & W_{\{q, k\}}^{(22)}
\end{array}\right)\left(\begin{array}{c}
x_m^{(1)} \\
x_m^{(2)}
\end{array}\right)
后面两项的乘积本质就是向量
q (或
k )的两个二维行向量。
当向量维度为
d 时(
d 为偶数),则可以扩展为:
f_{\{q, k\}}\left(\boldsymbol{x}_m, m\right)=\boldsymbol{R}_{\Theta, m}^d \boldsymbol{W}_{\{q, k\}} \boldsymbol{x}_m
\boldsymbol{R}_{\Theta, m}^d=\left(\begin{array}{ccccccc}
\cos m \theta_1 & -\sin m \theta_1 & 0 & 0 & \cdots & 0 & 0 \\
\sin m \theta_1 & \cos m \theta_1 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & \cos m \theta_2 & -\sin m \theta_2 & \cdots & 0 & 0 \\
0 & 0 & \sin m \theta_2 & \cos m \theta_2 & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2} & -\sin m \theta_{d / 2} \\
0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2} & \cos m \theta_{d / 2}
\end{array}\right)
每两个为一组二维向量,一共有
d/2 个组合,可以直接拼接作为
d 维度的旋转位置编码。
二维扩展到多维的解读:Transformer升级之路:4、二维位置的旋转式位置编码 - 科学空间|Scientific SpacesTransformer升级之路:6、旋转位置编码的完备性分析 - 科学空间|Scientific Spaces
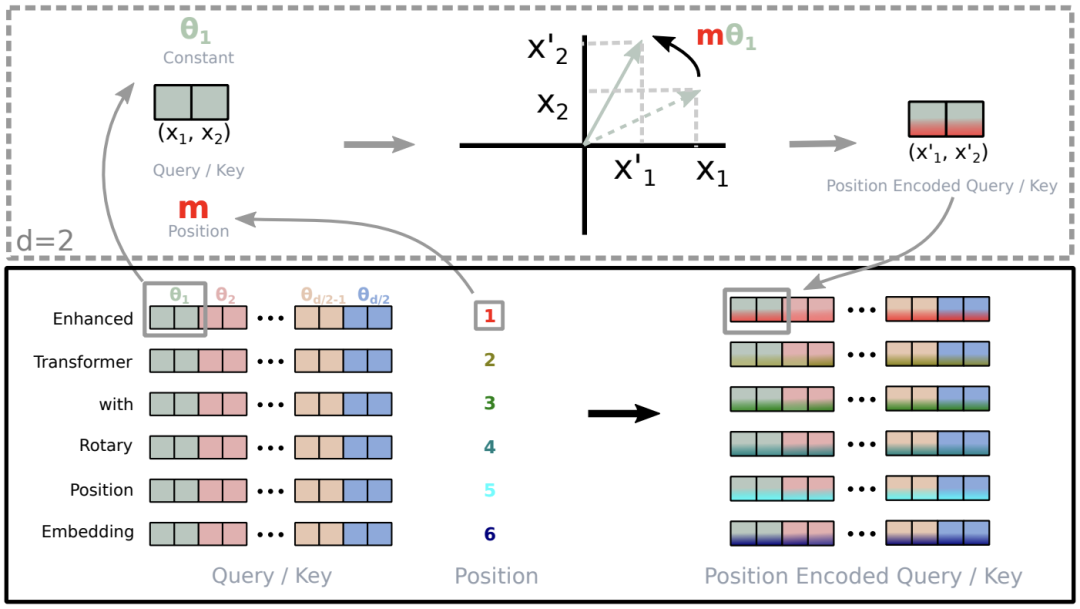
2.2 RoPE的实现 当输入一个句子“Enhanced Transformer with Rotary Position Embedding”时,首先获得其Query和Key向量q、 k,其对应的维度均为d,然后对于向量中相邻两个元素为一组,可以得到 d/2组(图中左下部分相同颜色的两个元素作为一组,对于每一组,一个文本则可以得到两个行向量); 获得每个词的绝对位置编号(该句子由6个词,位置编号分别为1,2,3,4,5,6),假设取“Enhanced”单词为例,其第一组元素为θ1,位置为 m=1,那么通过旋转位置编码可以的到新的元素值 x_1^{\prime}, x_2^{\prime} 。
所有单词的d/2个组合都按照这种形式进行“旋转”,即可得到新的位置编码(右下角) RoPE一种线性的实现如下所示:
\left(\begin{array}{c}
q_0 \\
q_1 \\
q_2 \\
q_3 \\
\vdots \\
q_{d-2} \\
q_{d-1}
\end{array}\right) \otimes\left(\begin{array}{c}
\cos m \theta_0 \\
\cos m \theta_0 \\
\cos m \theta_1 \\
\cos m \theta_1 \\
\vdots \\
\cos m \theta_{d / 2-1} \\
\cos m \theta_{d / 2-1}
\end{array}\right)+\left(\begin{array}{c}
-q_1 \\
q_0 \\
-q_3 \\
q_2 \\
\vdots \\
-q_{d-1} \\
q_{d-2}
\end{array}\right) \otimes\left(\begin{array}{c}
\sin m \theta_0 \\
\sin m \theta_0 \\
\sin m \theta_1 \\
\sin m \theta_1 \\
\vdots \\
\sin m \theta_{d / 2-1} \\
\sin m \theta_{d / 2-1}
\end{array}\right)
RoPE的性质 (1)远程衰减
从图中我们可以可以看到随着相对距离的变大,内积结果有衰减趋势的出现。因此,选择
\theta_i=10000^{-2 i / d} ,确实能带来一定的远程衰减性。当然,能带来远程衰减性的不止这个选择,几乎任意的光滑单调函数都可以。如果以
\theta_i=10000^{-2 i / d} 为初始化,将
θ_i 视为可训练参数,然后训练一段时间后发现
θ_i 并没有显著更新,因此干脆就直接固定
\theta_i=10000^{-2 i / d} 了。
(2)优势
用一个旋转矩阵rotation matrix来对绝对位置进行编码,于此同时,meanwhile; 在自注意力机制中导入显式的位置依赖。 自由的序列长度; 随着相对位置的增大,而逐步延缓退化(=衰减)的inter-token dependency; 用相对位置编码来“武装”线性自注意力。 具体来说,RoPE 使用 旋转矩阵对绝对位置进行编码 ,同时将 显式的相对位置依赖性纳入自注意公式中 。
【核心的两个点,一个是“旋转矩阵”,一个是“显式的相对位置依赖”】。
三、长文本外推性 外推性 的含义是在长文本表征过程中,如何在训练阶段只需要学习有限的长度,即可以在推理阶段能够延伸长度至若干倍且依然保持不错的性能和效果。
长度外推性是一个训练和预测的长度不一致的问题,主要体现在两个方面:
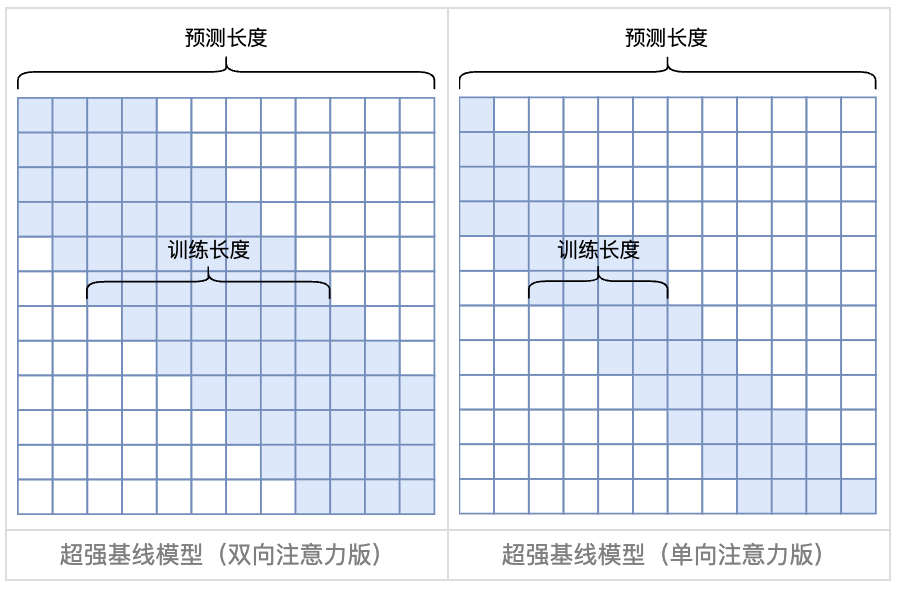
预测的时候用到了没训练过的位置编码(不论是绝对位置还是相对位置); 预测的时候注意力机制所处理的token数量远超训练时的数量。 解决长文本外推性问题的一个简单有效的方法是Attention Mask,如图所示:
通过类似滑动窗口的结构,约束一个每个token只能对局部区域的token计算Attention值,因此对于相对位置大小不会超过窗口大小,解决了第一个问题; Attention只会在窗口内计算,避免了对大量的token的Attention进行加权平均导致最终权重过度“平滑”现象。 在实现过程中,本质上是在计算完
\mathbf{q}_m^T \mathbf{k}_n 之后减去一个矩阵,即
\mathbf{q}_m^T \mathbf{k}_n-M ,其中
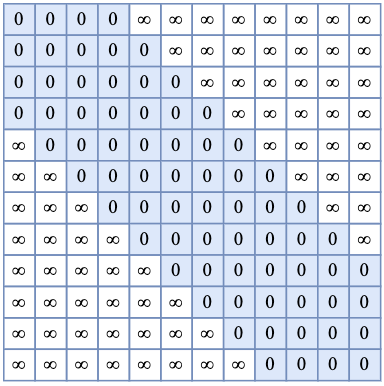
M 的形状如下图所示:
可以看出,蓝色区域(即滑动窗口内的局部区域)为0,说明保持原始的Attention归一化前的值;其他区域则为一个INT内最大的整数,说明Attention值是一个非常小的数(在softmax归一化后几乎为0)。
3.1 ALIBI 论文:《Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation》
其与上面的思想一样,只是改进了上面的 M矩阵为
λ ∣ m − n ∣ ,即Attention在归一化前的计算为:
\mathbf{q}_m^T \mathbf{k}_n-\lambda|m-n| ,其中
\lambda>0 为超参数,Transformer的多头注意力中的每个头的值可设置不同。矩阵
λ ∣ m − n 的形状如下所示:
相比于原始的方法,相对距离越长,
λ ∣ m − n ∣ 值就越大,越远的位置Attention值被归一化后就约小,相对于“滑动窗口”采用的方法是hard(在窗口内就计算attention,不在窗口内不计算),AIBLI是比较soft的(离得近attention就会比较大,离得远就比较小)。
3.2 KERPLE 论文:《KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation》
其对ALIBI进行了一些改进,引入了两个可学习的参数
r_1 和
r_2 来“动态”学习局部区域。如下图所示,左侧为原始的
\mathbf{q}_m^T \mathbf{k}_n ,通过引入参数来动态减去AIBLI中的
λ ∣ m − n ∣ 矩阵:
定义了两种模式,分别是power和logarithmic,分别对应没有对数和有对数的形式:
在logarithmic模式中,
r_1 控制了整体的量,
r_2 相当于ALIBI中的
\lambda , c是一个常数。苏神版简化写作:
3.3 Sandwich 论文:《Receptive Field Alignment Enables Transformer Length Extrapolation》
Sandwich与KEPRLE是同一个作者提出的,其对KEPRLE进行了少量改进,即对应的公式改写为:
\mathbf{q}_m^T \mathbf{k}_n+\lambda \mathbf{p}_m^T \mathbf{p}_n ,其中
p_m 和
p_n 可以使用Sinusoidal编码表示,即:
由于Sinusoidal编码在单调性上等价于
∣m−n∣ ,都是线性递增形式,因此Sandwich只是改头换面了。
3.4 XPOS 论文:《A Length-Extrapolatable Transformer》
参考解读:Transformer升级之路:7、长度外推性与局部注意力
其在RoPE的基础上引入了局部注意力。RoPE的本质是:
\boldsymbol{q}_m \rightarrow \boldsymbol{\mathcal { R }}_m \boldsymbol{q}_m, \quad \boldsymbol{k}_n \rightarrow \boldsymbol{\mathcal { R }}_n \boldsymbol{k}_n
其中:
\boldsymbol{\mathcal { R }}_n=\left(\begin{array}{cc}
\cos n \theta & -\sin n \theta \\
\sin n \theta & \cos n \theta
\end{array}\right)
在第2大节中已经介绍了RoPE是通过使用复数来实现绝对位置表示相对位置的。XPOS通过引入一个新的标量
\xi ,即有:
\begin{aligned}
&\boldsymbol{q}_m \rightarrow \boldsymbol{\mathcal { R }}_m \boldsymbol{q}_m \xi^m, \quad \boldsymbol{k}_n \rightarrow \boldsymbol{\mathcal { R }}_n \boldsymbol{k}_n \xi^{-n}\\
&\left(\boldsymbol{\mathcal { R }}_m \boldsymbol{q}_m \xi^m\right)^{\top}\left(\boldsymbol{\mathcal { R }}_n \boldsymbol{k}_n \xi^{-n}\right)=\boldsymbol{q}_m^{\top} \boldsymbol{\mathcal { R }}_{n-m} \boldsymbol{k}_n \xi^{m-n}
\end{aligned}
由于RoPE相对位置是
m−n ,而不是
∣m−n∣ ,因此XPOS约束在了单向Transformer,从而避免了负数出现。
XPOS又设计了一个局部感知的注意力机制Blockwise Causal Attention,进一步提升了局部注意力的性能,提升了长文本的外推性。
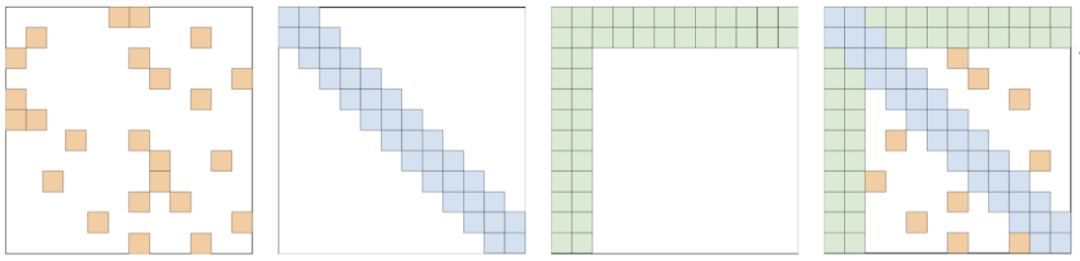
四、外推性的其他探索 (1)混合注意力Mask 在解决长文本位置表征时,典型的代表有Transformer-XL、BigBird、LongFormer,他们除了局部注意力机制以外,还引入了随机位置的性质:
如上图,第2张图为局部注意力(滑动窗口),第3章图为有限的全局感知(例如只限制前两个token可以看见所有的token)。而第一张图则是随机mask,以缓解过度hard的局部注意力。三者注意力混合起来后得到第四张图,这也是普遍训练超长文本大模型时采用的方法。
(2)随机位置表征 论文:《Randomized Positional Encodings Boost Length Generalization of Transformers》
绝对位置表征时,会存在位置上的OOV问题,随机位置编码则是通过在训练过程中采用如下策略:
对应的代码也很简单:
def random_position_ids(N, L=2048):
"""从[0, L)中随机不重复挑N个整数,并从小到大排列
"""
return np.sort(np.random.permutation(L)[:N])
苏神对随机位置编码的新探索:
对应的代码为:
def random_position_ids(N):
"""先随机采样n,然后从[0, n]均匀取N个点
"""
n = sample_from_xxx()
return np.linspace(0, 1, N) * n
(3) log n Attention Scale
原始的Attention计算公式为:
\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V
只需要简单的改成下面即可:
\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{\log _m n}{\sqrt{d_k}} Q K^T\right) V
其中
m 是训练时的最大长度,
n 是预测时的位置,通常来说
n>>m 。直觉来看,就是直接在计算
QK^T 时,根据其相对位置来控制Attention的值。当
m 和
n 距离很远时,
log_{m}n 的值会很大,会使得整体Attention归一化后会比较平缓,有助于解决外推性问题。
(4)全局依赖 滑动窗口的方法如果在一层Transformer Layer里看,本质上类似长度为
w 的N-Gram模型,即如下图所示:
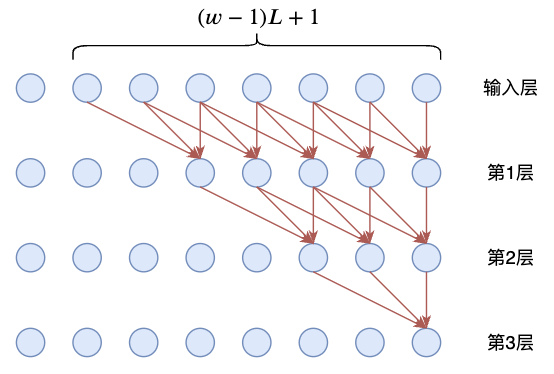
如果Transformer又
L 层,那么,从输入层开始,长度为
w 的窗口内的信息,可以在经过
L 层之后传给一个更广的区域,区域长度为
(w − 1) L + 1 ,如下图所示:
苏神给出的一种新的想法,就是假设我有
L 层Transformer,则可以在前
L − 1 层利用这种扩张特性,得到最终
(w-1)(L-1)+1 长度的区域后,在最后一层采用上面提到的 logn Attention Scale方法,讲前
L−1 层扩张的信息快速在最后一层与所有token进行交互。引入苏神的原文为:
这种局部注意力+Attention Scale的结合也是一种很巧妙的idea。实验也发现这种策略的外推性很惊艳。