参变量变分原理(1)

fem178

发布于 2024-01-29 18:15:25

1210

发布于 2024-01-29 18:15:25

文章被收录于专栏：数值分析与有限元编程数值分析与有限元编程

参变量变分原理

如图1所示的拉杆，刚度为

，其势能表达式为

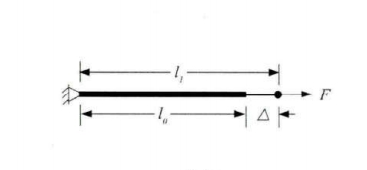
\Pi = \frac{1}{2}K \Delta^2 - F\Delta \quad\cdots (1)

▲图1

求此泛函极值即为经典变分原理。另一方面，求极值也可看做是最优控制，即二次优化问题。经典变分原理只能解决一类简单的最优控制问题,因为它只能在无约束条件下是有效的。而实际上更多的是属于有约束的一类最优控制问题。对于力学中的一些问题,如弹塑性分析、接触问题分析等,经典变分法在处理这类问题时将会受到一定的限制，需要借助参变量变分原理，注意和广义变分原理的区别。

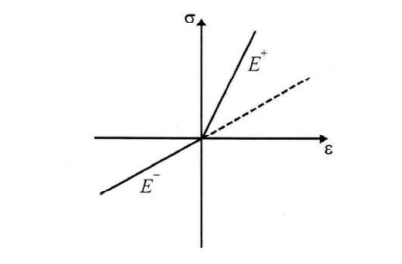
▲图2

图2所示，若材料具有双线性本构关系，杆件处于拉伸状态时的弹性模量为

E^+

,(对应的刚度为

K^+

);当其处于压缩状态时，弹性模量为

E^-

(对应的刚度为

K^-

)。其物理方程可表示为:

\begin{split} F&=K^+ \Delta , \Delta \geq 0\\ F&=K^- \Delta , \Delta \leq 0 \end{split}

具有拉压不同弹性模量的杆件,求解算法较为复杂。基于参变量变分原理求解此类问题的基本思路是通过构造杆件在拉、压两种应力状态下的统一本构方程来避免算法执行过程中弹性模量的刚性选择，进而将问题转换为二次规划问题来求解。下面我们将详细讲述拉、压不同模量杆件的参变量统一本构方程的建立。选取

K^+ > K^-

的情况进行推导，而

K^+ < K^-

的情况同理可得。对分别处于拉伸和压缩两种应力状态的杆件，我们考虑始终选取其压缩刚度

K^-

来建立本构方程。对于处于压缩状态的杆件而言，压缩刚度自然反映的是杆件的真实变形和应力状态;而对于处于拉伸状态的杆件而言，由于杆件的真实变形状态本应由其拉伸刚度来描述，所以当选取压缩刚度来计算其变形时会引入一个附加伸长量

\lambda

。我们把

\lambda

称作参数变量，其物理意义如图3所示。

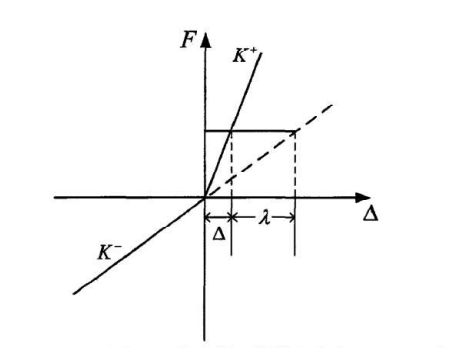
▲图3

注意到此时有

F>0,\Delta>0

，参数变量

\lambda

与伸长量

\Delta

、外载

之间的关系可表示为:

\Delta = \frac{F}{K^+} = \frac{F}{K^-} + \lambda \quad \cdots (2)

(2)也可写为

F = K^-(\Delta + \lambda ) \quad \cdots (3)

其中

\lambda = \begin{cases} 0, & \text{$\Delta$ < 0} \\ \frac{K^+ - K^-}{K^-}\Delta, & \text{$\Delta$ $\geq$ 0} \end{cases}\quad\cdots (4)

(3)和(4)为杆件的参变量统一本构方程。由式(4)可以发现，参数变量

\lambda

表征了杆件所处的实际应力状态。具体地，当杆件受压缩短时，

\lambda=0

，式(3)即为杆件受压时的本构方程;而杆件受拉伸长时，

\lambda= \frac{K^+ - K^-}{K^-}\Delta

，将其代入式(3)并整理化简后，可得

F=K^+\Delta

，即杆件受拉时的本构方程。这表明，统一本构方程式(3)完全等价于问题原始的非线性弹性本构方程。此外，还不难发现

\lambda\geq0

总是成立的。实际分析时，我们只需计算表征杆件当前应力状态参数变量

\lambda

即可，无需关注弹性模量变化。

为方便数值求解，我们可对式(4)作进一步的推导。首先，将式(4)的第二式整理为:

(K^+ - K^-)\Delta - K^- \lambda =0,(\Delta\geq0,\lambda >0) \quad \cdots (5)

应注意的是，式(5)只在

\Delta\geq0

的条件下成立;而当

\Delta<0

时，式(5)不能成立。当

\Delta<0

时，由于

\lambda =0

，且事先我们已假定

K^+ > K^-

，即

K^+ - K^- >0

，应有:

(K^+ - K^-)\Delta - K^- \lambda \leq0,(\Delta<0,\lambda =0) \quad \cdots (6)

为将式(5)和(6)统一起来，引入一个非负的松弛变量

\nu

，可得:

\begin{split} \nu - K^- \lambda + (K^+ - K^-)\Delta &= 0 \\ \lambda\geq0,\nu\geq0,\lambda\nu&=0\\ \end{split} \quad \cdots (7)

式(7)中，

\lambda\geq0

和

\nu\geq0

表明非负条件;而

\lambda\nu=0

为互补条件，它意味着,

\lambda,\nu

两个非负变量中，至少有一个为零，也可以同时为零。具体可分为以下三种情形:

(1)当

\lambda=0,\nu=0

时，有

\Delta = 0

，表明杆件既不伸长，也不缩短，处于未变形状态;

(2)当

\lambda>0,\nu=0

时，有

\Delta > 0

，表明杆件伸长，处于拉伸状态;

(3)当

\lambda=0,\nu>0

时，有

\Delta < 0

，表明杆件缩短，处于压缩状态。

因此，式(7)是典型的状态控制方程，

\lambda

可理解为控制参数，表征了杆件处于拉、压两种应力状态下的附加伸长量:杆件受压或未变形时，此附加伸长量

\lambda

为零;件受拉时，此附加伸长量为

\lambda= \frac{K^+ - K^-}{K^-}\Delta

。

有了以上推导以后，我们便可以建立拉、压不同模量杆件和图1拉杆的参数最小势能原理(参变量变分原理)。利用式(3)，可以写出单根杆件的含有参数变量的势能表达式：

\Pi = \frac{1}{2}K^-( \Delta+\lambda)^2 - F\Delta \quad \cdots (8)

不过该势能表达式并不能独立存在，而需要附加上互补方程组(7)才能准确地描述问题的物理含义:在状态控制方程(式(7))的约束下，真实的位移解总是使得系统的势能(式(8))取最小值。概括起来，单根拉、压不同模量杆件的参变量变分原理可表达为:

\begin{split} min.\quad \Pi = \frac{1}{2}K^-( \Delta+\lambda)^2 - F\Delta \\ s.t. \quad\nu - K^- \lambda + (K^+ - K^-)\Delta &= 0 \\ \lambda\geq0,\nu\geq0,\lambda\nu&=0\\ \end{split} \quad \cdots (9)

根据参变量变分原理,通过对式(8)进行变分运算便可得到问题本身的平衡方程.具体地，参数变量

\lambda

不参与变分计算，而只对变量

\Delta

进行变分运算，可得:

F-K^-( \Delta+\lambda) =0 \quad \cdots (10)

显然，式(10)与式(3)等价，即杆件的平衡方程。求解时，无论杆件处于拉伸还是压缩状态,只需将由状态控制方程(7)解得的参数变量入代入平衡方程(10)便能解得杆件的变形量

\Delta

。

双线性模量的传统算法参见

双线性弹塑性模型(一)

双线性弹塑性模型(二)