数学建模--微分方程

在数学建模中，微分方程模型是一种极其重要的方法，广泛应用于各种实际问题的描述和解决。微分方程模型通过建立变量及其变化率之间的关系，可以预测和分析系统的行为。这些模型在科技、工程、生态、环境、人口、交通、医学、经济管理等各个领域都有广泛应用。

常见的微分方程模型

1. 常微分方程（ODE）：
   • 指数衰减模型：用于描述随时间减少而逐渐趋于零的过程。
   • 指数增长模型：用于描述随时间增加而迅速增长的过程。
   • Logistic生长模型：用于描述生物种群的增长，当资源有限时会达到一个饱和值。
   • SIR模型：用于流行病学中的传染病传播，包括易感者（Susceptible）、感染者（Infected）和移除者（ removed）三个部分。
2. 偏微分方程（PDE）：
   • 一维平流方程：描述流体或物质在空间中的移动。
   • 一维热传导方程：描述热量在物体内部的传递过程。
   • 二维双曲方程：用于描述波动现象，如声波和水波。
   • 二维抛物方程：常用于描述扩散过程，如气体分子在容器中的扩散。
   • 二维椭圆方程：用于描述静态平衡状态，如电势分布。
3. 其他类型的微分方程模型：
   • Lotka-Volterra模型：用于描述捕食者和猎物之间的动态关系。
   • 阻滞增长模型：用于描述由于资源限制导致的增长速度下降的现象。

微分方程建模的基本步骤

1. 确定研究对象：首先需要明确要研究的量（自变量、未知函数、必要参数），并确定坐标系统。
2. 建立基本规律：根据实际问题的特点，找出变量之间的基本规律，并列出相应的微分方程。
3. 求解微分方程：对于能够求得解析解的微分方程，可以直接求解；对于复杂的微分方程，则需要利用数值方法进行近似求解。
4. 模型验证与调整：将求解结果与实际情况进行对比，分析其一致性，并根据需要对模型进行修正和优化。

代码示例

常微分方程

import numpy as np
from scipy.integrate  import odeint

# 定义常微分方程的函数
def model(y, t):
    dydt = -2 * y  # 以 dy/dt = -2y为例
    return dydt

# 设置初始条件
y0 = 1

# 设置时间点
t = np.linspace (0, 5, 100)

# 求解常微分方程
solution = odeint(model, y0, t)

# 输出结果
print(solution)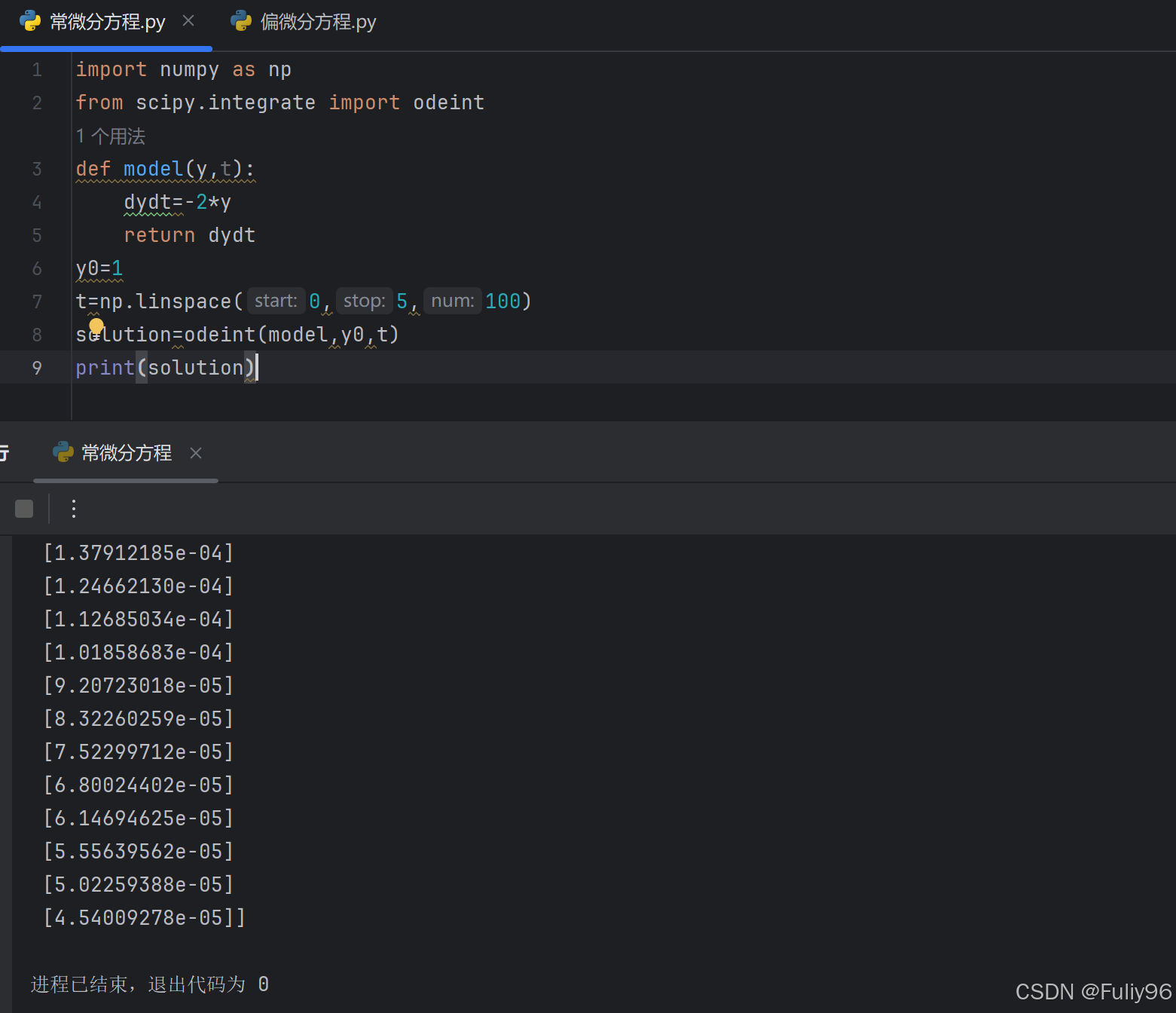

偏微分方程

import numpy as np
from numba import vectorize

# 定义有限差分法求解泊松方程的函数
@vectorize(['float64(float64, float64, float64, float64)'], target='cpu')
def laplacian(center, top, left, right):
    return (top + left + right - 3 * center)

# 初始化网格大小和步长
N = 100
h = 1 / N

# 创建初始网格
grid = np.random.rand(N, N)

# 迭代求解泊松方程
for _ in range(100):  # 迭代次数可以根据需要调整
    new_grid = grid.copy()
    for i in range(1, N-1):
        for j in range(1, N-1):
            new_grid[i, j] += h**2 * laplacian(grid[i, j], grid[i-1, j], grid[i, j-1], grid[i, j+1])
    grid = new_grid

print(grid)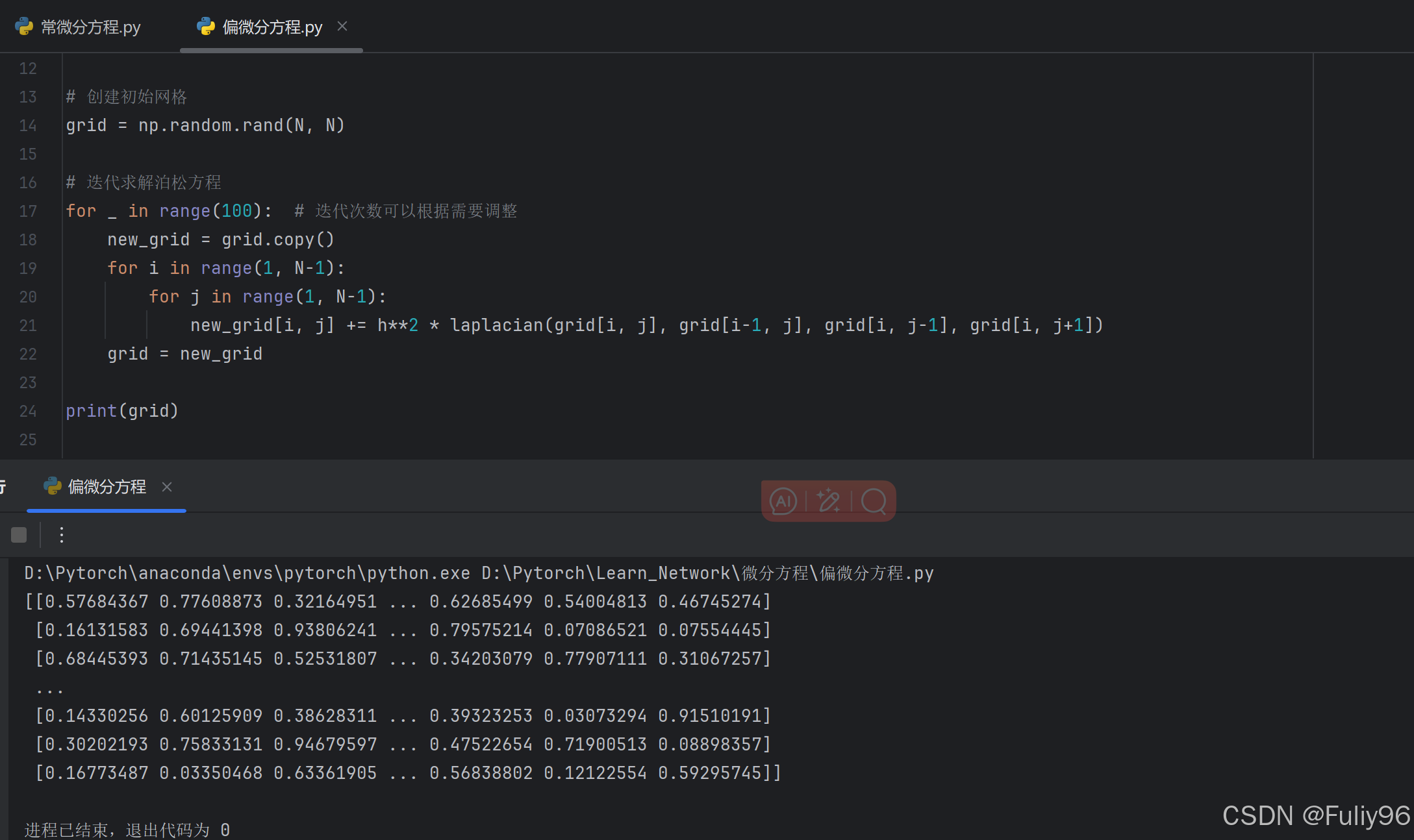

应用实例

• 人口增长模型：Malthus模型是一个典型的常微分方程模型，用于描述人口随时间的变化规律。
• 流行病学模型：SIR模型通过微分方程描述了易感者、感染者和移除者的动态变化过程。
• 物理学中的热传导问题：通过偏微分方程描述热量在物体内部的传递过程。

结论

微分方程模型在数学建模中具有重要地位，它不仅能够全面深刻地揭示实际事物内在的动态关系，还能帮助我们做出相应的决策或对未来进行预测。通过合理选择和应用不同的微分方程模型，可以有效地解决各类实际问题，提高建模的准确性和实用性。

如何在数学建模中准确识别和选择合适的微分方程模型？

在数学建模中，准确识别和选择合适的微分方程模型需要遵循一定的步骤和方法。以下是详细的指导： 首先，理解实际问题的核心目标和约束条件是至关重要的。这一步骤包括明确问题的背景、目的以及需要解决的具体问题。 分析题目属于哪一类问题，并确定可以使用的微分方程模型类型。例如，在生物学中，布朗运动可以用随机微分方程模拟，心脏电信号可以用一般微分方程模拟。 根据规律列方程或利用已知的定理与规律寻找变量之间的关系式。这可以通过数学、力学、物理、化学等学科中的定理或经过实验检验的规律来实现。此外，还可以使用微元分析法，通过已知的定理与规律寻找微元之间的关系式。 在各种领域里，人们已经建立了一些经典的微分方程模型，熟悉这些模型对建模有帮助。例如，交通图、地质图、航空模型和建筑模型等都可以用不同的微分方程来描述。 建立初步模型后，需要进行验证和调整。可以通过实验数据或已有的理论知识来检验模型的准确性，并根据结果进行必要的修改。 最后，将模型应用于实际问题中，并不断优化以提高其准确性和适用性。例如，在工程领域，工程师通常会关注几个集成量，如桥梁的最大位移或飞机的基本周期等。

微分方程模型在解决实际问题中的应用案例有哪些？

微分方程模型在解决实际问题中有着广泛的应用，以下是一些具体案例： 微分方程在生物学中的应用非常广泛。例如，通过建立种群增长模型，可以预测不同物种的种群数量变化。这些模型通常使用指数增长或逻辑斯蒂增长方程来描述生物种群随时间的变化。 在物理学中，微分方程用于描述各种物理现象。例如，导热微分方程用于描述物体内部的热传导过程，这在工程和材料科学中有重要应用。另外，纳维-斯托克斯方程是流体力学中的一个经典例子，它被用于天气预报和气象学研究。 微分方程在几何学中也有应用，比如悬链线问题。悬链线是指由自重作用下形成的曲线，这类问题可以通过求解适当的微分方程来解决。 在经济学中，微分方程可以用来建模经济变量如价格、产量等随时间的变化。例如，通过建立供需模型，可以预测市场上的价格波动。 药物扩散衰减模型是一个典型的医学应用案例。通过建立药物在人体内的扩散和代谢模型，可以优化药物的剂量和给药方案，以达到最佳治疗效果。 微分方程在航空工程中的应用之一是飞机减速伞的设计。通过建立伞翼的空气动力学模型，可以计算出最佳的伞翼形状和展开速度，从而确保飞机安全着陆。 在刑事侦查领域，微分方程也可以用于构建犯罪行为的数学模型，帮助警方追踪和预测犯罪模式。 以上这些案例展示了微分方程在不同学科中的广泛应用及其重要性。

常微分方程（ODE）与偏微分方程（PDE）在数学建模中的优缺点分别是什么？

在数学建模中，常微分方程（ODE）和偏微分方程（PDE）各有其优缺点。

常微分方程（ODE）的优缺点

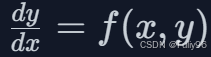
优点：

1. 简单易懂：常微分方程的形式相对简单，易于理解和使用。
2. 描述变化规律：常微分方程能够描述函数随时间的变化规律，这在物理学中尤为重要，如物体运动轨迹、电路中电流变化等。通过求解这些方程，可以预测变化趋势，为问题解决提供依据。
3. 模型精度较高：由于温度变化常微分方程是基于实际物理现象建立的，因此其模型精度较高。
4. 广泛应用于工程和科学领域：常微分方程在工程和科学领域有广泛应用，例如在电路分析、机械振动等方面。

缺点：

1. 解析解难以求得：大部分的常微分方程无法求出精确的解析解，只能得到近似解。
2. 初始条件的近似性：用来描述物理过程的微分方程以及由试验测定的初始条件也是近似的，这种近似之间的影响和变化必须在理论上加以解决。

偏微分方程（PDE）的优缺点

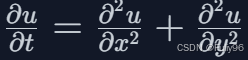
优点：

1. 强大的工具：偏微分方程的数值解法提供了一种强大的工具来解决那些难以直接求解的问题，在科学研究和工程应用中扮演着至关重要的角色。
2. 广泛的应用范围：偏微分方程可用于建模实际问题，例如天气预报、飞机设计、赛车速度等。
3. 现代计算技术的支持：随着计算技术的进步，偏微分方程的数值方法在准确性、效率和可用性方面不断提高，使得它们在解决现代复杂问题中更加有效。
4. 深度学习的应用：深度学习方法可以捕捉到“藏在数据下面”的物理信息，准确度比传统的PDE离散方程高得多，并且省去了传统方法中需要对PDE构造不同复杂离散网格的步骤。

缺点：

1. 求解难度大：解析方法仅适用于少数特定类型的偏微分方程，大多数情况下需要依赖数值方法。
2. 精度受网格影响：数值方法的精度受网格细度的影响较大，如果网格划分不够精细，则可能导致结果不准确。
3. 理论研究复杂：偏微分方程理论的研究涉及解的存在性、解的数量、解的各种性质以及求解方法等多个方面，这些研究通常非常复杂。

总结来说，常微分方程在描述单变量函数随时间变化时具有优势，但其解析解往往难以求得；

在进行微分方程模型求解时，哪些数值方法最有效，且如何选择最适合的问题类型？

在进行微分方程模型求解时，选择最有效的数值方法取决于微分方程的类型和复杂性。以下是一些常用的数值方法及其适用问题类型的详细说明： 欧拉法是最简单的数值求解方法之一，通过将微分方程中的导数用差分代替来近似求解。它适用于初值问题，并且容易实现，但其精度较低，收敛速度较慢，不适合要求高精度的问题。 改进的欧拉法是欧拉法的一种改进版本，通过引入中点法来提高精度。它同样适用于初值问题，比欧拉法有更高的精度和更快的收敛速度。 龙格-库塔法是一类广泛使用的高精度数值方法，包括一阶、二阶、四阶等不同形式。其中，四阶龙格-库塔法是最常用的一种，具有很高的精度和稳定性，适用于各种初值问题和边值问题。 多步法如Adams方法和Gear方法，通过利用前几步的信息来计算下一步的值，从而提高计算效率和精度。这些方法特别适合于需要长时间积分的问题。 有限差分法通过将微分方程离散化为代数方程组来求解。这种方法适用于偏微分方程的定解问题，如椭圆型方程、抛物线型方程和双曲型方程。 梯度下降法主要用于非线性微分方程的优化问题，通过迭代更新解的位置以最小化目标函数。该方法在处理非线性问题时非常有效，但可能需要较长的计算时间。

如何选择最适合的问题类型

对于线性微分方程，可以使用积分方法直接求解。如果需要数值解，则可以选择欧拉法或改进的欧拉法。 非线性微分方程通常难以找到解析解，因此需要采用数值方法。龙格-库塔法和多步法是较好的选择，因为它们具有较高的精度和稳定性。 偏微分方程的数值求解通常采用有限差分法或有限元法。有限差分法适用于定解问题，而有限元法则适用于边界值问题。 初值问题一般推荐使用龙格-库塔法或多步法，因为这些方法能够提供较高的精度和稳定性。 边值问题可以使用有限差分法或有限元法进行求解，特别是对于复杂的几何形状和边界条件。 总之，在选择数值方法时，应根据具体问题的性质（如线性或非线性）、求解精度要求以及计算资源等因素综合考虑。例如，对于需要高精度和稳定性的复杂问题，龙格-库塔法和多步法是较好的选择；

数学建模中微分方程模型的最新研究进展有哪些？

在数学建模中，微分方程模型的最新研究进展主要集中在以下几个方面： 南京大学戴万阳教授团队在倒向随机偏微分方程（DSDEs）与机器学习金融大模型的研究上取得了新突破。他们发展了新的方法和体系，用于大模型回归学习训练求解强非线性问题。 徐成喜、张健和姚佳烽等人构建了基于专家系统和神经常微分方程（DDEs）的延迟混合模型，并将其应用于疾病进展预测。相较于传统的微分方程（ODEs），DDEs能够更灵活地描述生物系统的动态过程，提高预测结果的可靠性。 研究者们构建了新型的人工神经网络，实现了更快地求解偏微分方程（PDEs）。经过训练后，这些神经网络不仅可以求解单个PDE，而且可以无需再度训练即可求解整个PDE族。 在多尺度问题的长时间稳定数值模拟方面，非线性期望下的倒向随机微分方程（BSDEs）适定性研究也取得了进展。这为复杂系统如Vlasov-Maxwell模型提供了重要的理论支持。 运用微分方程系统来求解约束优化问题的研究也在不断深入。通过将Karush-Kuhn-Tucker (KKT) 条件转化为光滑方程组问题，研究者们探索了轨迹的存在性和收敛性。