教练！我的表需要校准吗？（YUNSWJ 分析版）

今天这个文章个人感觉是比较有实际意义的，昨天是使用了 SMU 检验设备，这是比较灵活的方式，但是对于衡量精度来说，我们应该使用基准源来测试。

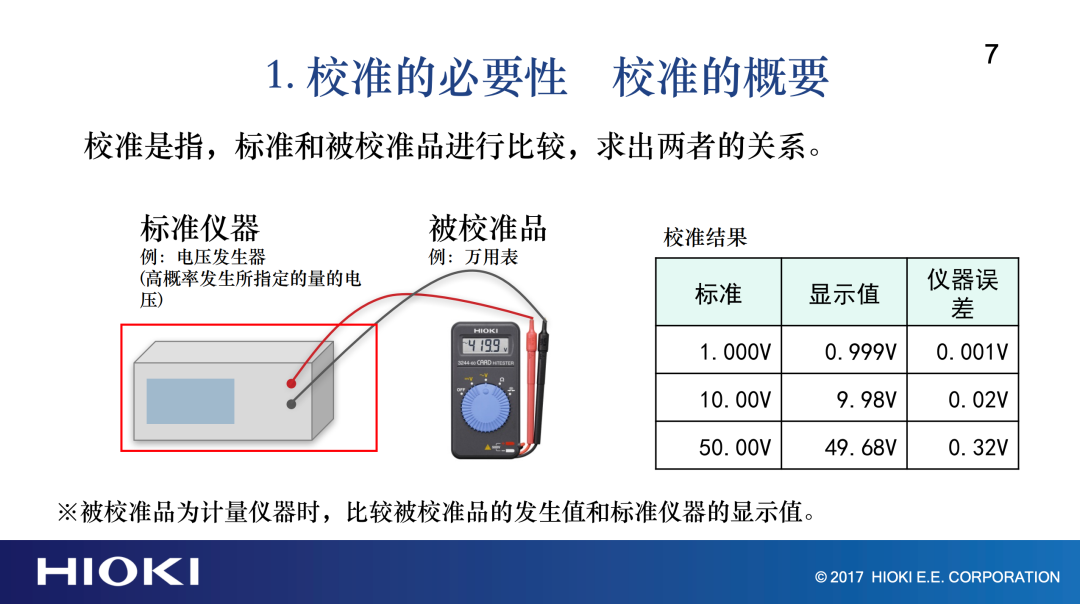
我们不校准，我们来判断现在需要校准吗？

我们不校准，我们来判断现在需要校准吗？

开始研究DM7275是否需要校准

我们基准源使用 LM399

我们基准源使用 LM399

最热也才 23 度，热量被隔绝在封装内部，有点火热了

最热也才 23 度，热量被隔绝在封装内部，有点火热了

然后仇老板的万用表也是七位半的：

笑死了，这表就跟被诅咒了，实物图都很模糊

笑死了，这表就跟被诅咒了，实物图都很模糊

然后我们假定仇老板的表是校准的，结果是可以可信的：

然后这样叠起来测试

然后这样叠起来测试

定义已知变量和测量误差

已知基准电压，这是 LM399 基准源 提供的理想值。

DM7275 测量值：

DMM7510 测量值：

测量误差：，

根据测量结果：

误差分析

根据误差定义，测量误差可以表示为：

误差测量值理论值理论值

对于 DM7275：

误差

对于 DMM7510：

误差

这表明 DM7275 和 DMM7510 的误差都在 0.18% 左右。

比较误差和测量精度

Hioki DM7275 的精度是 0.00005%（最小误差）。这意味着它的理论误差应该小于 0.00005%，远低于 0.18% 的误差。因此，DM7275 的测量精度应该是足够的，误差可能来自于 环境、接触电阻、测试线路 等外部因素，而非设备本身的故障。

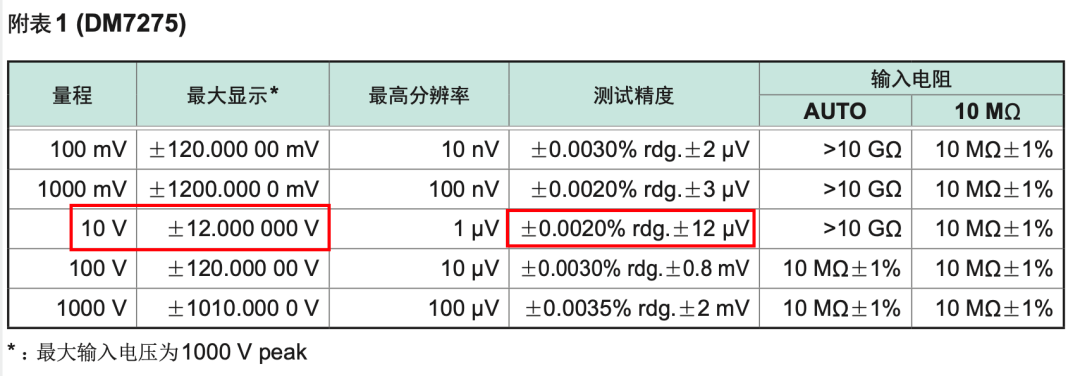
最高分辨率：设备在每个量程下的最小显示分辨率。

测量精度：各量程下的测量精度，表示设备的 测量误差。

在 10V 量程下，设备的精度为 ±0.0020%，这意味着DM7275 在该量程下的理论误差应为：

误差µ

这与我们测得的 Hioki DM7275 的测量误差（18.767 mV）相比，误差略大。显然，环境因素、接触电阻或其他因素可能导致实际测量误差偏大。（因为测量因素没有建模其他的）

要想非常准确，应该这样做，不过这也太鸡吧复杂了

要想非常准确，应该这样做，不过这也太鸡吧复杂了

量程与分辨率：

Hioki DM7275 在 10V 量程下的分辨率为 10 µV，这表明该设备能够精确显示到 微伏级别；对比之前的测量数据，Keithley 2450 和 Hioki DM7275 的测量值都在 0.18% 左右的误差范围，在精度上基本一致。

确定是否需要校准?

由于误差 0.18% 远高于设备的标称精度（通常在万分之一到百万分之一级），我们可以提出以下假设：如果 DM7275 和 DMM7510 的测量误差一致，且这种误差在多次测量中保持稳定，那么问题很可能来自于外部环境影响，而不是 DM7275 的设备故障。

不确定度分析

假设 DM7275 的测量精度为0.00005%，而当前的误差为0.1877%，这意味着设备存在 大约 3-4 级别的误差放大。此时可以使用以下模型来估算不确定度：

不确定度误差设备精度倍误差

这个不确定度值非常高，说明误差的主要来源可能是 设备外部因素，而不是设备本身。

统计学的意义

以上是单独的数值给的结论，现在用上统计数据：

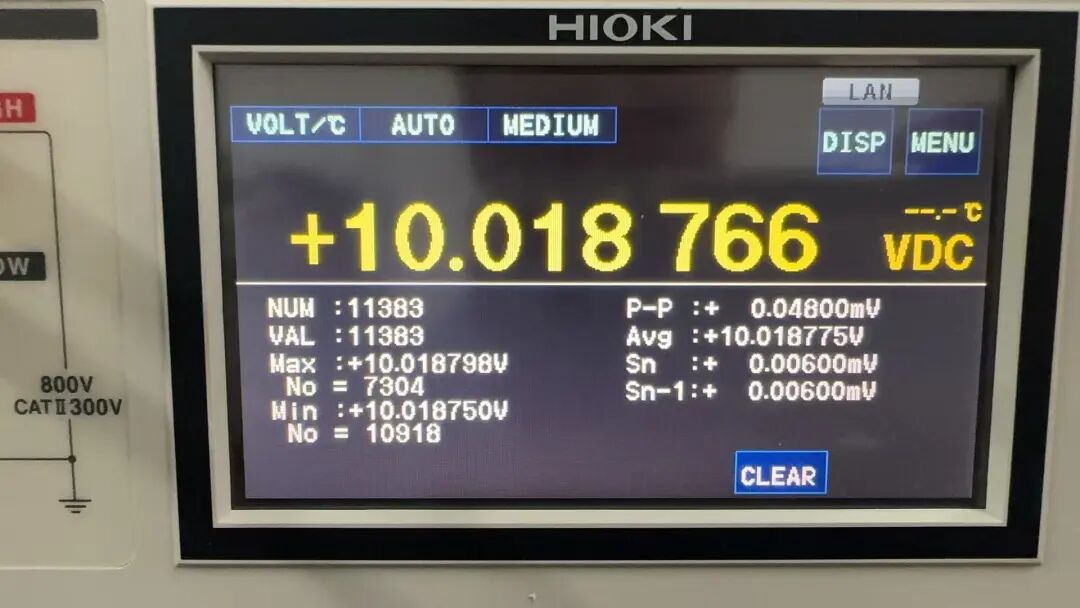
日置的

日置的

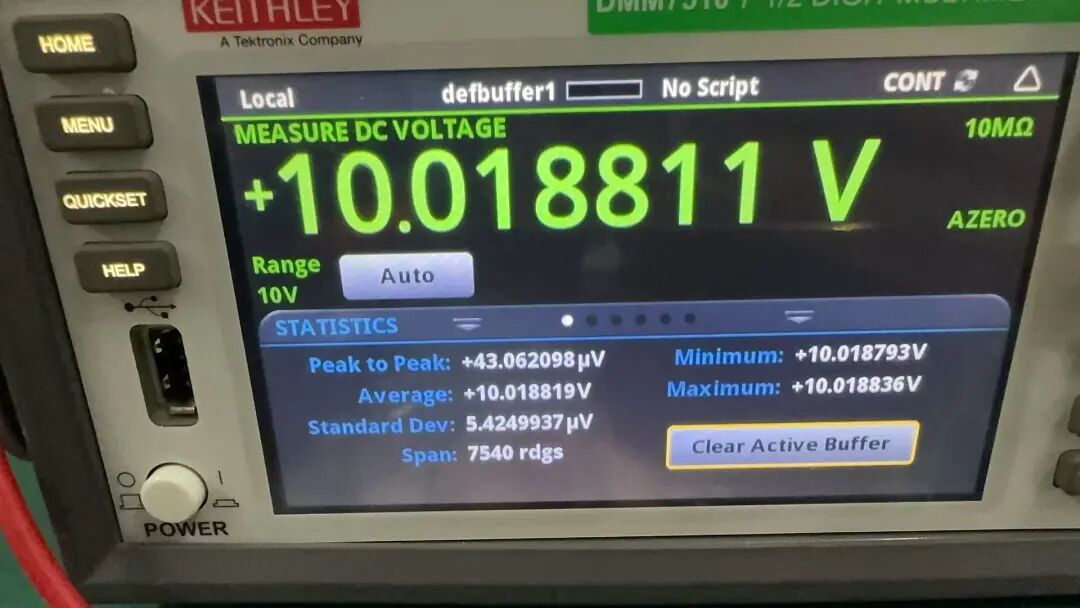
是德

是德

Hioki DM7275 测量数据

测量值：10.018766 V

最大值：10.018798 V

最小值：10.018750 V

P-P（峰峰值）：±48.00 µV

平均值：10.018775 V

标准偏差（Sn）：±6.00 µV

Keithley 2450 测量数据

测量值：10.018811 V

最大值：10.018836 V

最小值：10.018793 V

P-P（峰峰值）：±43.06 µV

平均值：10.018819 V

标准偏差（Sn）：±5.42 µV

计算每个测量值的误差

Hioki DM7275：

误差计算：

误差

其中，* 是 10 V 的基准电压。

误差

Keithley 2450：

误差计算：

误差

误差

比较误差和稳定性

根据计算结果：Hioki DM7275 的误差为 0.1877%，Keithley 2450 的误差为 0.1881%，这两个误差值非常接近，意味着这两台仪器的测量值几乎相同。

波动分析

P-P 值（峰峰值）：

Hioki DM7275：±48.00 µV

Keithley 2450：±43.06 µV

这些数据表明，Hioki DM7275 的波动稍大一些，但总体差异在 50 µV 以内。

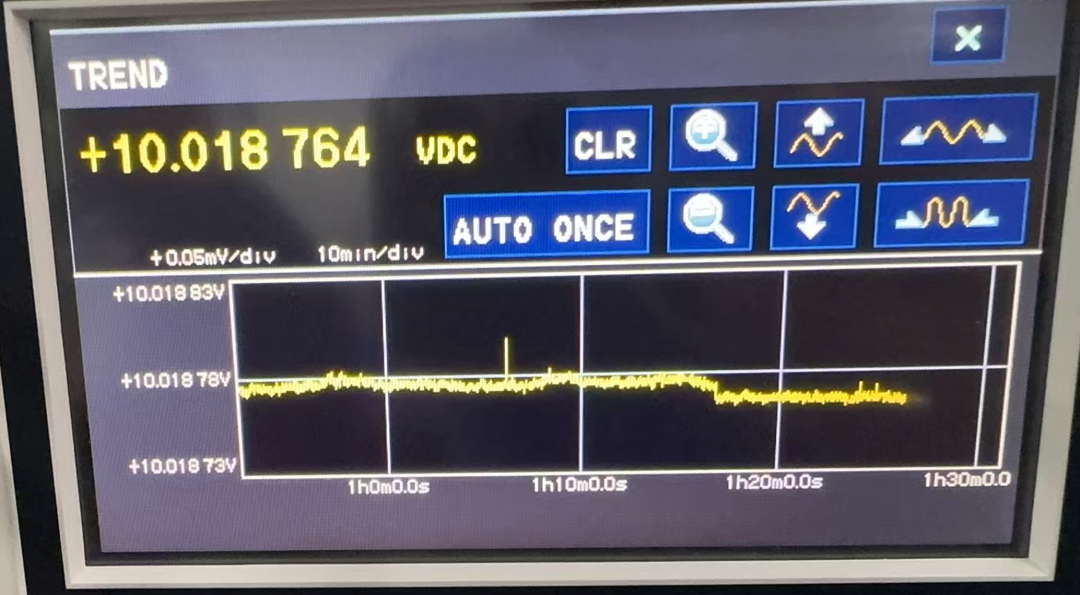
看图的话是有一些毛刺的

看图的话是有一些毛刺的

计算标准偏差（Sn）

Hioki DM7275 的 标准偏差（Sn） 为 6.00 µV

Keithley 2450 的 标准偏差（Sn） 为 5.42 µV

标准偏差越小，说明仪器的测量越稳定，因此 Keithley 2450 的稳定性略好于 Hioki DM7275。

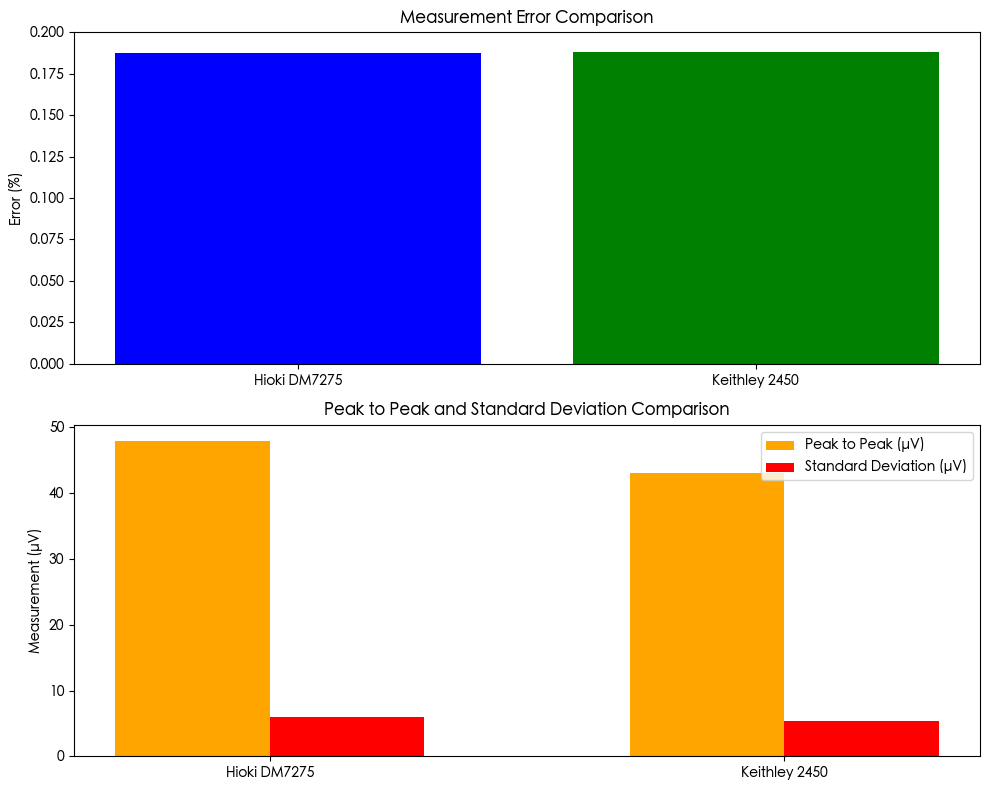
测量误差比较：Hioki DM7275 和 Keithley 2450 的误差非常接近，分别为 0.1877% 和0.1881%，都非常小，说明它们的测量精度相似。

峰峰值（P-P）与标准偏差（Sn）比较：

Hioki DM7275 的 峰峰值（P-P） 为 48 µV，而 Keithley 2450 的 峰峰值（P-P） 为 43.06 µV，显示 Hioki DM7275 的波动略大一些。

标准偏差：Hioki DM7275 的 标准偏差（Sn） 为 6 µV，而 Keithley 2450 的 标准偏差（Sn） 为 5.42 µV，显示 Keithley 2450 稍微更稳定。

对比测量的稳定性和误差

在 P-P 值 和 标准偏差 的比较上，Keithley 2450 的测量结果略优于 Hioki DM7275；在测量的 误差 和 波动 上，两者几乎相同，因此可以认为 DM7275 的性能已经非常接近 Keithley 2450。

由于误差和波动非常接近，而且 两台仪器的测量误差都在 0.18% 左右，所以 DM7275 目前的测量精度已经非常接近标准，且误差范围很小。因此，DM7275 不需要校准，除非需要 极高的精度要求 或在 长期使用后检测到 测量误差增大。

后记：

如果 DMM7510 是经过校准的，并且在同样条件下测量，那么它提供的电压值已经非常可靠，且 DM7275 的测量结果与其几乎完全一致，也就是说可以在当前的测量环境下认为它已足够精确，不需要管了！enjoy！感谢仇老板的测试。

import matplotlib.pyplot as plt
import numpy as np

# Data for Hioki DM7275 and Keithley 2450
instruments = ['Hioki DM7275', 'Keithley 2450']
errors = [0.1877, 0.1881]  # Measured errors in percentage
peak_to_peak = [48.00, 43.06]  # Peak to peak values in microvolts
std_dev = [6.00, 5.42]  # Standard deviation in microvolts

# Create a figure and axis for subplots
fig, ax = plt.subplots(2, 1, figsize=(10, 8))

# Plot error comparison
ax[0].bar(instruments, errors, color=['blue', 'green'])
ax[0].set_title('Measurement Error Comparison')
ax[0].set_ylabel('Error (%)')
ax[0].set_ylim(0, 0.2)

# Plot peak-to-peak and standard deviation comparison
bar_width = 0.3
index = np.arange(len(instruments))

bar1 = ax[1].bar(index - bar_width/2, peak_to_peak, bar_width, label='Peak to Peak (µV)', color='orange')
bar2 = ax[1].bar(index + bar_width/2, std_dev, bar_width, label='Standard Deviation (µV)', color='red')

ax[1].set_title('Peak to Peak and Standard Deviation Comparison')
ax[1].set_ylabel('Measurement (µV)')
ax[1].set_xticks(index)
ax[1].set_xticklabels(instruments)
ax[1].legend()

# Display the plot
plt.tight_layout()
plt.show()