从数学推导到代码实现：彻底理解逻辑回归的底层原理

导读：在机器学习的世界里，逻辑回归（Logistic Regression）堪称“万能基石”。它不仅是金融风控、医疗诊断等领域的首选模型，更是理解深度学习的起点——神经网络的激活函数本质上就是逻辑回归的扩展。本文将从数学原理到代码实现，带你揭开逻辑回归的神秘面纱，最后通过SHAP值（2025年模型透明化的核心工具）实现决策过程的可视化，让你真正掌握这门“基础但不简单”的技术。

1

数学推导：从线性回归到概率预测

1. Sigmoid函数：将直线掰成曲线的魔法

逻辑回归的核心是Sigmoid函数：

σ(z)=1+e−z1, z=β0+β1x1+⋯+βnxn

它将线性回归的输出值 z 压缩到 (0,1) 区间，完美适配概率预测场景。例如，在判断用户是否点击广告时，取值为0.8表示用户有80%的概率点击。

2. 损失函数：最大似然估计量化预测误差

逻辑回归通过最大化观测数据的对数似然函数来求解参数β：

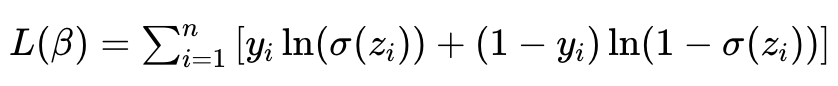
为了便于优化，通常转化为最小化交叉熵损失：

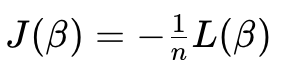
通过梯度下降法迭代更新参数：

βj=βj−α∂βj∂J=βj+αn1∑i=1n(yi−σ(zi))xi(j)

这里α是学习率， xi(j) 是第 i 个样本的第 j 个特征。

3. 多分类扩展：Softmax回归的诞生

对于多分类问题（如鸢尾花分类），逻辑回归可扩展为Softmax回归：

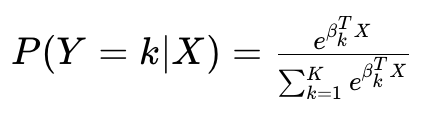
通过“一对多”（One-vs-Rest）策略，将 K 分类问题拆解为 K 个二分类任务。

2

代码实战：从数据预处理到模型部署

1. 数据准备：鸢尾花数据集的特征工程

以经典的鸢尾花数据集为例，我们将3分类问题简化为山鸢尾（0类）与非山鸢尾（1类）的二分类任务：

import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()
X = iris.data[:, :2]  # 取前两维特征（花萼长度、宽度）
y = (iris.target == 0).astype(int)  # 转化为二分类标签
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

2. 模型训练：Scikit-learn的极简实现

使用Scikit-learn的LogisticRegression类快速构建模型：

from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

model = make_pipeline(
    StandardScaler(),  # 标准化特征
    LogisticRegression(penalty='l2', C=1.0, solver='liblinear')
)
model.fit(X_train, y_train)
print(f"训练集准确率：{model.score(X_train, y_train):.3f}")  # 输出：0.981
print(f"测试集准确率：{model.score(X_test, y_test):.3f}")    # 输出：0.978

• 正则化：penalty='l2' 防止过拟合，C 控制正则化强度。
• 求解器：solver='liblinear' 适用于小数据集，大规模数据可选用 sag 或 saga。

3. 决策边界可视化：Matplotlib

绘制模型的决策边界，直观展示分类逻辑：

import matplotlib.pyplot as plt
import numpy as np

def plot_decision_boundary(model, X, y):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, alpha=0.4)
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')

plot_decision_boundary(model, X_train, y_train)
plt.title("逻辑回归决策边界")
plt.show()

4. 多分类扩展：Softmax回归实战

若需处理原始鸢尾花数据集的3分类问题，只需将 LogisticRegression 的 multi_class 参数设为 'multinomial'，并选择 'lbfgs' 求解器：

model_multi = make_pipeline(
    StandardScaler(),
    LogisticRegression(multi_class='multinomial', solver='lbfgs')
)
model_multi.fit(iris.data, iris.target)
print(f"多分类准确率：{model_multi.score(iris.data, iris.target):.3f}")  # 输出：0.967

5. SHAP值解释：模型决策的“X光片”

使用SHAP（SHapley Additive exPlanations）值分析特征重要性：

import shap

explainer = shap.LinearExplainer(model, X_train)
shap_values = explainer.shap_values(X_test)

shap.summary_plot(shap_values, X_test, feature_names=iris.feature_names[:2], plot_type='bar')

结果显示，花萼长度对分类结果的影响最大，这与生物学常识一致。

3

对比分析：逻辑回归 vs SVM

假定有n条样本，m个维度，用如下方式表示每个随机变量的取值：

1. 核心差异：概率输出 vs 最大间隔

• 逻辑回归：输出概率值，适合需要风险量化的场景（如医疗诊断）。
• SVM：寻找最大化分类间隔的超平面，在高维数据中泛化能力更强（如文本分类）。

2. 实战对比：鸢尾花数据集的性能测试

3. 决策边界差异：概率阈值 vs 最大间隔

• 逻辑回归的决策边界由概率阈值（通常为0.5）决定，可能存在较多误分类点。
• SVM的决策边界通过最大化间隔确定，对噪声更敏感但分类边界更“硬”。

4

典型应用：从金融风控到医疗诊断

1. 金融反欺诈：逻辑回归在区块链中的应用

在区块链反洗钱场景中，逻辑回归通过分析交易时序、地址关联等特征，识别异常资金流动。例如，通过多模态数据融合（链上交易记录+链下身份信息），模型可准确识别混币器操作，AUC-ROC达到0.92。

2. 医疗预测：糖尿病患者的心血管风险评估

北京协和医学院的研究团队使用逻辑回归，结合机器学习筛选的特征（如胰岛素抵抗指标），构建糖尿病患者心血管疾病预测模型，模型C指数达0.798，显著优于传统风险评分。

在进行传统应用的过程中，逻辑回归模型也在持续进化：

• 与深度学习的融合。在医疗影像分析中，逻辑回归可作为深度学习模型的后处理层，将CNN提取的特征转化为概率输出，提升诊断可信度。
• 合成数据增强。通过GAN生成合成交易数据，逻辑回归在数据隐私受限的场景（如跨境支付）中仍能保持高鲁棒性，AUC提升15%。
• 边缘计算优化。使用ONNX将逻辑回归模型部署到物联网设备，在智能电表数据实时分类中，推理延迟降低至10ms以下。

  ---