问SciPy Delaunay三角剖分因参数的微小变化而改变单纯形的多个点
EN

Stack Overflow用户

提问于 2021-09-07 12:40:38

回答 1查看 241关注 0票数 1

我使用Delaunay三角剖分来插值在一个规则的四维网格上的一组参数上计算的函数值。有时，当一个参数值发生少量的变化，从而使它变成一个新的单纯形时，单形中的多个点会发生变化。我希望，由于我不断地改变一个参数，我会从单纯形移动到单纯形，一次只改变单形中的一个点(通常在我的代码中也是这样)。相反，请考虑以下脚本：

import numpy as np
from scipy.spatial import Delaunay

# hideous construction to get the desired 4d grid of points
# with points at [-1, -0.5, 0, 0.5, 1] along each axis
X = np.vstack(list(map(np.ravel, np.meshgrid(*[np.linspace(-1, 1, 5) for i in range(4)])))).T

tri = Delaunay(X)

delta = 1e-10

print(np.sort(tri.vertices[tri.find_simplex([-0.25, -0.05, 0.5+delta, 0.1])]))
print(np.sort(tri.vertices[tri.find_simplex([-0.25, -0.05, 0.5-delta, 0.1])]))

产

[192 292 317 318 322]
[167 292 293 313 317]

请注意，这两个简单点相差3分，我期望有一个，而且我还没有设计出一个二维或三维的例子，其中多个顶点会发生变化。

我99%肯定这是因为我的观点是在一个规则的网格上，但我找不到一个详细的答案，为什么或如何避免这个问题。我知道三角剖分并不是唯一的，但这根本不是一个问题。各种技巧似乎改变了我在哪里遇到这个问题，但我还没有找到一个“修复”，防止问题出现在任何地方。

编辑

我在3D中找到了一个例子，这让我可以想象出这个问题。

import numpy as np
from scipy.spatial import Delaunay

X = np.vstack(list(map(np.ravel, np.meshgrid(*[np.linspace(-1, 1, 5) for i in range(3)])))).T
tri = Delaunay(X)

delta = 1e-6
x = np.array([-0.25, 0, 0.07])

fig = pl.figure()
ax = fig.add_subplot(projection='3d')

ax.scatter(*x, c='k')

x[1] = delta
s = X[tri.vertices[tri.find_simplex(x)]]

for i, si in enumerate(s):
    for j, sj in enumerate(s[i:]):
        ax.plot3D(*np.vstack([si, sj]).T, c='C0')

x[1] = -delta
s = X[tri.vertices[tri.find_simplex(x)]]
for i, si in enumerate(s):
    for j, sj in enumerate(s[i:]):
        ax.plot3D(*np.vstack([si, sj]).T, c='C1')

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_zlabel('$z$')

这是输出的两个方面。

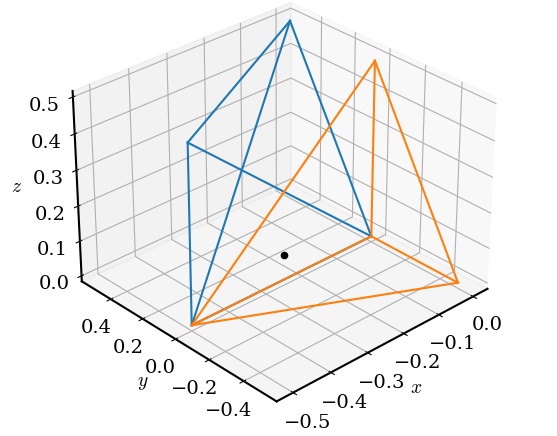
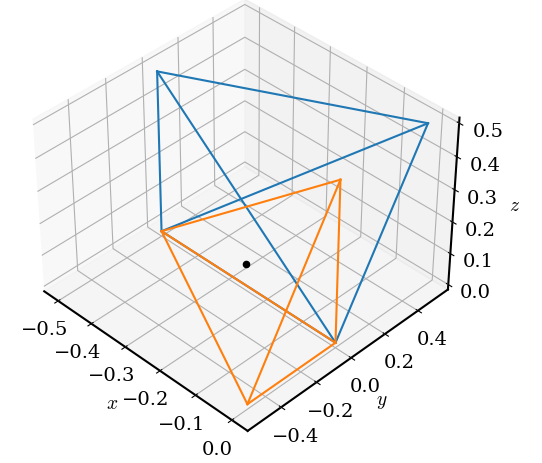
蓝色和橙色的简单点是包含插值点之前和之后，它跨越y=0 (从正到负)。我的假设是，这两个简单元素沿着y=0平面都会有相同的三角形面，但这显然是不正确的。这是Delaunay三角剖分在这个退化的情况下的基础，还是关于实现的一些东西？有什么办法可以避免吗？QHull选项Qx (在SciPy的默认选项中用于D>4)似乎对本例有所帮助，但我不确定全局的情况。

scipy-spatial

python

scipy

delaunay

回答 1

Stack Overflow用户

发布于 2021-09-07 23:35:08

您的问题并不是关于在scipy.spatial中实现三角剖分。更多的是关于Delaunay三角剖分作为数学对象的数学。

. defined =‘defined 1’>维D中的Delaunay三角剖分定义得很好.当点是“一般位置”时。这意味着输入点上没有D+2点在公共球面上。如果发生这种情况，有人说Delaunay三角剖分是“退化的”。当三角剖分退化时，Delaunay三角剖分没有很好的定义，在保持Delaunay性质的同时，存在多种方法对点的凸包进行三角剖分。

您所观察到的是:您的点位于一个常规网格上，这是一个非常退化的点集(用于Delaunay属性)。任何对坐标的轻微修改都会触发多个简单操作的翻转，从而恢复Delaunay属性。

也许您可以通过查看Delaunay三角剖分的双重对象来理解这种行为:它的Voronoi图。对于接近规则网格的点集，图是退化的:它有长度为零的Voronoi边，或者长度接近于零。对点坐标的任何小修改都会改变Voronoi图的拓扑结构(因此也会改变Delaunay三角剖分)。

票数 0

页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持

原文链接：

https://stackoverflow.com/questions/69094334

复制

Windows凭据不工作

云服务器 windows server windows

如果不是敲错IP、用户名、密码，报凭据不工作，一般情况下执行这几句命令后重启远程服务就正常了

Windows技术交流

2021/06/15