星多边形圆环碰撞-解决速度方向上的交点&确定碰撞侧
摘要
这个问题是用JavaScript写的,但是用任何语言、伪代码或者仅仅是数学的答案都是很棒的!
我一直在尝试实现分离-轴定理以完成以下工作:
- 检测凸多边形与圆之间的交点。
- 找出一个可以应用于圆圈的平移来解析交点,这样圆圈几乎没有接触到多边形,而不再在里面。
- 确定碰撞的轴线(问题结束时的细节)。
我已经成功地完成了第一个要点,您可以在问题的末尾看到我的javascript代码。我对其他部分有困难。
解析交
关于如何在圆周的最小/最短重叠方向上求解交点的问题,网上有很多例子。从我的代码中可以看到,在最后,我已经计算过了。
不过,这不符合我的需要。我必须解决碰撞在相反的方向圆的轨迹(假设我已经有圆的轨迹,并希望把它作为一个单位向量或角度,无论适合我的函数)。
在下面的图像中,您可以看到最短分辨率与预期分辨率之间的区别:
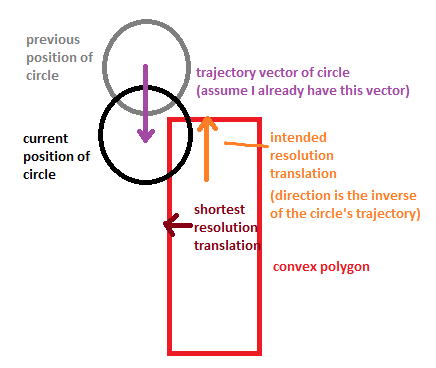
如何计算出test_CIRCLE_POLY函数中求交的最小平移向量,但它要应用于一个特定的方向,与圆圈的轨迹相反?
我的想法/尝试:
- 我的第一个想法是在SAT算法中必须测试的轴上增加一个附加轴,这个轴将垂直于圆的轨迹。然后,当投影到这个轴上时,我将根据重叠进行解析。这将是一种工作,但在大多数情况下会解决问题。它不会导致最小的翻译。所以这是不令人满意的。
- 我的第二个想法是继续使用最短重叠的大小,但将方向改变为与圆圈轨迹相反的方向。这看起来很有希望,但可能有很多边缘的情况,我还没有说明。也许这是个很好的开始。
确定碰撞的侧/轴
我想出了一种方法来确定这个圆圈与哪一边的多边形发生碰撞。对于每个被测试的多边形轴,我只需检查是否重叠。如果有重叠,那一侧就会发生碰撞。
这个解决方案将不能再一次被接受,因为我只想找出一个方面取决于圆圈的轨迹。
我想要的解决方案会告诉我,在下面的例子中,A轴是碰撞的轴,而不是B轴。这是因为一旦解决了交点,A轴就是与多边形一侧对应的轴,而多边形的一侧几乎不接触圆。

我的想法/尝试:
- 目前,我假设碰撞的轴是垂直于MTV (最小平移向量)。这目前是不正确的,但是一旦我在问题的前半部分更新了交集解析过程,就应该是正确的轴。因此,这部分应该首先处理。
- 或者,我考虑从圆的前一个位置和它们当前的位置+半径创建一条线,并检查哪一边与这条线相交。然而,仍然存在模糊性,因为有时会有多个边与线相交。
到目前为止我的代码
function test_CIRCLE_POLY(circle, poly, circleTrajectory) {
// circleTrajectory is currently not being used
let axesToTest = [];
let shortestOverlap = +Infinity;
let shortestOverlapAxis;
// Figure out polygon axes that must be checked
for (let i = 0; i < poly.vertices.length; i++) {
let vertex1 = poly.vertices[i];
let vertex2 = poly.vertices[i + 1] || poly.vertices[0]; // neighbouring vertex
let axis = vertex1.sub(vertex2).perp_norm();
axesToTest.push(axis);
}
// Figure out circle axis that must be checked
let closestVertex;
let closestVertexDistSqr = +Infinity;
for (let vertex of poly.vertices) {
let distSqr = circle.center.sub(vertex).magSqr();
if (distSqr < closestVertexDistSqr) {
closestVertexDistSqr = distSqr;
closestVertex = vertex;
}
}
let axis = closestVertex.sub(circle.center).norm();
axesToTest.push(axis);
// Test for overlap
for (let axis of axesToTest) {
let circleProj = proj_CIRCLE(circle, axis);
let polyProj = proj_POLY(poly, axis);
let overlap = getLineOverlap(circleProj.min, circleProj.max, polyProj.min, polyProj.max);
if (overlap === 0) {
// guaranteed no intersection
return { intersecting: false };
}
if (Math.abs(overlap) < Math.abs(shortestOverlap)) {
shortestOverlap = overlap;
shortestOverlapAxis = axis;
}
}
return {
intersecting: true,
resolutionVector: shortestOverlapAxis.mul(-shortestOverlap),
// this resolution vector is not satisfactory, I need the shortest resolution with a given direction, which would be an angle passed into this function from the trajectory of the circle
collisionAxis: shortestOverlapAxis.perp(),
// this axis is incorrect, I need the axis to be based on the trajectory of the circle which I would pass into this function as an angle
};
}
function proj_POLY(poly, axis) {
let min = +Infinity;
let max = -Infinity;
for (let vertex of poly.vertices) {
let proj = vertex.projNorm_mag(axis);
min = Math.min(proj, min);
max = Math.max(proj, max);
}
return { min, max };
}
function proj_CIRCLE(circle, axis) {
let proj = circle.center.projNorm_mag(axis);
let min = proj - circle.radius;
let max = proj + circle.radius;
return { min, max };
}
// Check for overlap of two 1 dimensional lines
function getLineOverlap(min1, max1, min2, max2) {
let min = Math.max(min1, min2);
let max = Math.min(max1, max2);
// if negative, no overlap
let result = Math.max(max - min, 0);
// add positive/negative sign depending on direction of overlap
return result * ((min1 < min2) ? 1 : -1);
};回答 4
Stack Overflow用户
发布于 2020-06-20 07:35:15
我假设多边形是凸的,圆是沿着一条直线移动的(至少在一段可能很小的时间间隔内是这样),而不是遵循一些弯曲的轨迹。如果它遵循的是弯曲的轨迹,那么事情就变得更加困难。在曲线轨迹的情况下,可以保留基本思想,但实际的碰撞点(圆的碰撞分辨率点)可能更难计算。尽管如此,我还是提出了一个想法,这个想法也可以推广到那个案子。另外,它还可以作为圆与凸多边形碰撞检测的主要方法。
我没有考虑所有可能的情况,其中可能包括特殊或极端的情况,但至少它给你一个方向去探索。
将圆与多边形的碰撞转化为圆心(点)与圆圆半径r加厚的多边形的一个版本之间的碰撞,即:(i)多边形的每个边沿垂直于多边形的向量r向外偏移(翻译),并指向多边形外;(ii)顶点成为半径r的圆弧,以多边形顶点为中心,连接适当偏置边的端点(基本上,在多边形顶点处放置半径r圆并取其凸包)。
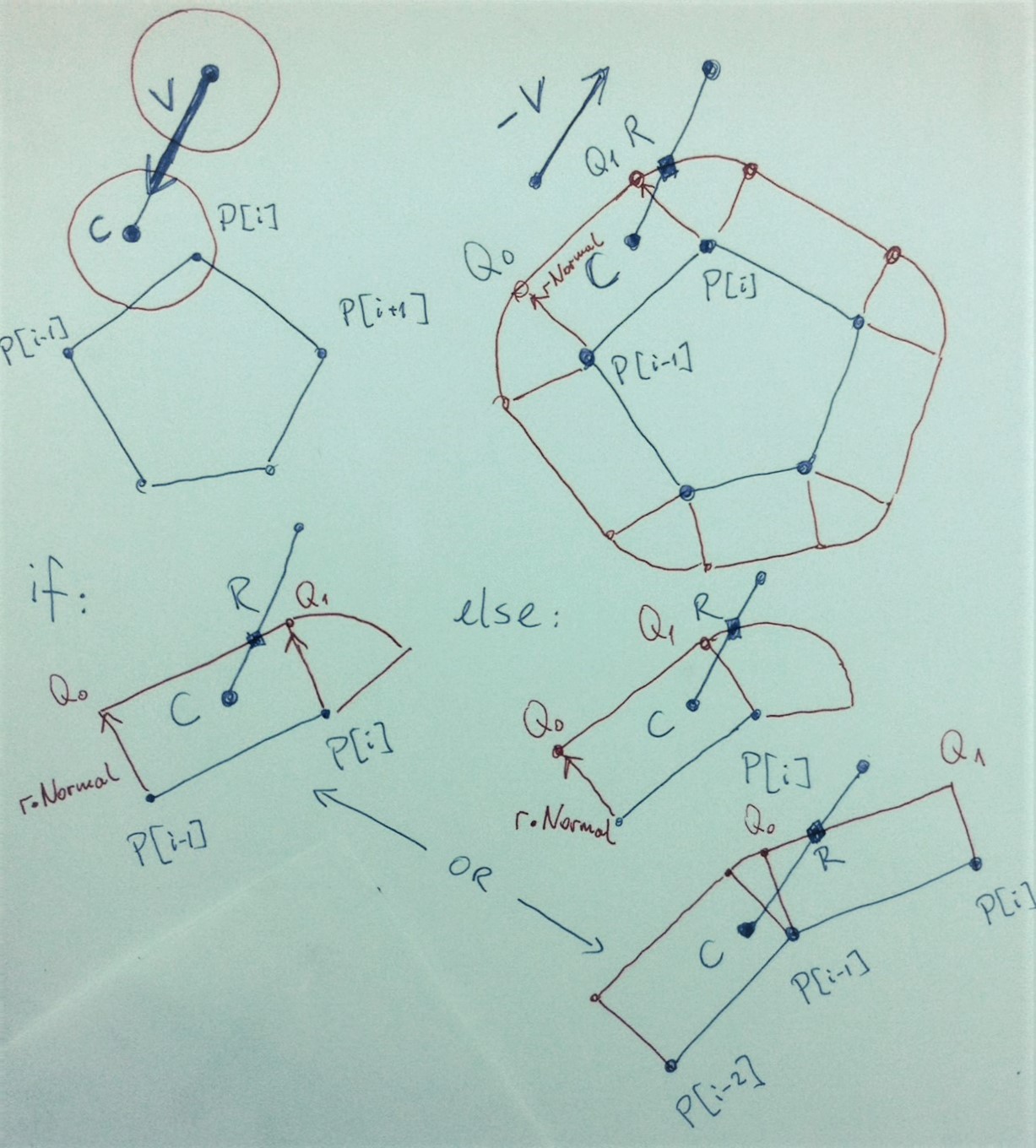
现在,圆心的当前位置是C = [ C[0], C[1] ],它一直沿着一条直线移动,方向矢量V = [ V[0], V[1] ]指向运动方向(或者如果您愿意的话,可以将V看作是检测到碰撞时圆圈的速度)。然后,有一个由向量方程X = C - t * V定义的轴(或者说射线--一条有向的半线),其中t >= 0 (这个轴指向过去的轨迹)。基本上,这是通过中心点C并与/平行于向量V的半条线。现在,分辨率点,也就是你想把你的圆移动到的点,就是X = C - t * V轴与加厚多边形的边界相交的点。
因此,你必须检查(1)第一个轴交点的边,然后(2)轴交点与圆弧形,属于原始多边形的顶点。
假设多边形是由一个顶点阵列,P = [ P[0], P[1], ..., P[N], P[0] ]定向逆时针方向。
(1)对于原始多边形的每个边缘P[i-1]P[i],与您的碰撞相关(这些可能是在检测碰撞的顶点处相遇的两个相邻的边缘,或者在圆圈以非常快的速度移动的情况下,它实际上是所有的边缘,而且您检测到碰撞的时间很晚,所以实际的碰撞甚至没有在那里发生,这由您决定,因为您更了解您的情况的细节)。您有以下输入数据:
C = [ C[0], C[1] ]
V = [ V[0], V[1] ]
P[i-1] = [ P[i-1][0], P[i-1][1] ]
P[i] = [ P[i][0], P[i][1] ]做:
Normal = [ P[i-1][1] - P[i][1], P[i][0] - P[i-1][0] ];
Normal = Normal / sqrt((P[i-1][1] - P[i][1])^2 + ( P[i][0] - P[i-1][0] )^2);
// you may have calculated these already
Q_0[0] = P[i-1][0] + r*Normal[0];
Q_0[1] = P[i-1][1] + r*Normal[1];
Q_1[0] = P[i][0]+ r*Normal[0];
Q_1[1] = P[i][1]+ r*Normal[1]; 为s, t求解线性方程组(相交方程):
Q_0[0] + s*(Q_1[0] - Q_0[0]) = C[0] - t*V[0];
Q_0[1] + s*(Q_1[1] - Q_0[1]) = C[1] - t*V[1];如果0<= s <= 1和t >= 0,您就完成了,并且您的解决方案是
R[0] = C[0] - t*V[0];
R[1] = C[1] - t*V[1];否则
(2)对于与碰撞相关的每个顶点的,做以下操作:为t求解二次方程(有一个显式公式)
norm(P[i] - C + t*V )^2 = r^2或扩大:
(V[0]^2 + V[1]^2) * t^2 + 2 * ( (P[i][0] - C[0])*V[0] + (P[i][1] - C[1])*V[1] )*t + ( P[i][0] - C[0])^2 + (P[i][1] - C[1])^2 ) - r^2 = 0或者,如果您更喜欢以类似代码的方式:
a = V[0]^2 + V[1]^2;
b = (P[i][0] - C[0])*V[0] + (P[i][1] - C[1])*V[1];
c = (P[i][0] - C[0])^2 + (P[i][1] - C[1])^2 - r^2;
D = b^2 - a*c;
if D < 0 there is no collision with the vertex
i.e. no intersection between the line X = C - t*V
and the circle of radius r centered at P[i]
else
D = sqrt(D);
t1 = ( - b - D) / a;
t2 = ( - b + D) / a;
where t2 >= t1 那么你的决心是
R[0] = C[0] - t2*V[0];
R[1] = C[1] - t2*V[1];Stack Overflow用户
发布于 2020-06-20 07:24:36
这可能不是你想要的,但这里有一种方法(如果你不是在寻找完美的精确度):
您可以尝试近似的位置,而不是计算它。
设置代码的方式有一个很大的优势:在碰撞之前,您拥有圆圈的最后位置。由于这一点,您可以在轨迹中“迭代”,并尝试找到一个最接近交集位置的位置。我假设你已经有了一个函数,它告诉你一个圆是否与多边形相交。代码(C++):
// What we need :
Vector startPos; // Last position of the circle before the collision
Vector currentPos; // Current, unwanted position
Vector dir; // Direction (a unit vector) of the circle's velocity
float distance = compute_distance(startPos, currentPos); // The distance from startPos to currentPos.
Polygon polygon; // The polygon
Circle circle; // The circle.
unsigned int iterations_count = 10; // The number of iterations that will be done. The higher this number, the more precise the resolution.
// The algorithm :
float currentDistance = distance / 2.f; // We start at the half of the distance.
Circle temp_copy; // A copy of the real circle to "play" with.
for (int i = 0; i < iterations_count; ++i) {
temp_copy.pos = startPos + currentDistance * dir;
if (checkForCollision(temp_copy, polygon)) {
currentDistance -= currentDistance / 2.f; // We go towards startPos by the half of the current distance.
}
else {
currentDistance += currentDistance / 2.f; // We go towards currentPos by the half of the current distance.
}
}
// currentDistance now contains the distance between startPos and the intersection point
// And this is where you should place your circle :
Vector intersectionPoint = startPos + currentDistance * dir;我还没有测试过这段代码,所以我希望没有大的错误。它也没有被优化,而且这种方法也有一些问题(交点可能在多边形内结束),所以它仍然需要改进,但我想你明白了。另一个问题(很大,取决于你在做什么)是,这是一个近似,而不是一个完美的答案。
希望这能帮上忙!
Stack Overflow用户
发布于 2020-06-20 13:48:16
圆多边形截距
如果球是移动的,如果你能确保球总是从多边形开始,那么解决方案就相当简单。
我们将把球和它的运动称为球线。它从球的当前位置开始,在球的位置结束,球将在下一帧。
要解决这个问题,你要找到离球线最近的截距。
有两种类型的拦截。
- 线段(球线)与线段(多边形边)
- 有圆的线段(球线)(在每个(仅凸的)多边形角处圆)
示例代码有一个Lines2对象,它包含两个相关的拦截函数。截取作为包含两个单位距离的Vec2返回。截距函数用于行(无限长),而不是行sgement。如果没有拦截,则返回未定义。
对于截取Line2.unitInterceptsLine(line, result = new Vec2())的行,单位值(以result表示)是从一开始沿每条线的单位距离。负值是背后的原因。
考虑球半径,每个多边形边沿其法向偏移球半径。重要的是多边形边缘有一个一致的方向。在这个例子中,法线在直线的右边,多边形点在顺时针方向。
对于截取Line2.unitInterceptsCircle(center, radius, result = new Vec2())的线段/圆,单位值(以result表示)是其拦截圆的直线上的单位距离。result.x将始终包含最近的拦截(假设您从圆圈之外开始)。如果有一个拦截,总是有两种方式,即使他们是在同一点。
示例
该示例包含所需的所有内容。
感兴趣的对象是ball和poly。
ball定义了球及其运动。还有为示例绘制它的代码。poly持有多边形的点。根据球半径将点转换为偏移线。它是优化的,它只计算线时,球半径的变化。
函数poly.movingBallIntercept是完成所有工作的函数。它接受一个球对象和一个可选的结果向量。
如果它与多边形接触,它将返回作为球的Vec2的位置。
它通过找到与偏移线的最小单位距离和点(作为圆)来实现这一点,并使用该单位距离来定位结果。
注意到,如果球在多边形内,截取的角就会反转。函数Line2.unitInterceptsCircle确实提供了两个单位的距离,在那里,直线进入和退出圆圈。但是,您需要知道您是在内部还是外部,以了解使用哪一个。该示例假设您位于多边形之外。
使用说明
- 移动鼠标以改变球的路径。
- 单击以设置球的起始位置。
Math.EPSILON = 1e-6;
Math.isSmall = val => Math.abs(val) < Math.EPSILON;
Math.isUnit = u => !(u < 0 || u > 1);
Math.TAU = Math.PI * 2;
/* export {Vec2, Line2} */ // this should be a module
var temp;
function Vec2(x = 0, y = (temp = x, x === 0 ? (x = 0 , 0) : (x = x.x, temp.y))) {
this.x = x;
this.y = y;
}
Vec2.prototype = {
init(x, y = (temp = x, x = x.x, temp.y)) { this.x = x; this.y = y; return this }, // assumes x is a Vec2 if y is undefined
copy() { return new Vec2(this) },
equal(v) { return (this.x - v.x) === 0 && (this.y - v.y) === 0 },
isUnits() { return Math.isUnit(this.x) && Math.isUnit(this.y) },
add(v, res = this) { res.x = this.x + v.x; res.y = this.y + v.y; return res },
sub(v, res = this) { res.x = this.x - v.x; res.y = this.y - v.y; return res },
scale(val, res = this) { res.x = this.x * val; res.y = this.y * val; return res },
invScale(val, res = this) { res.x = this.x / val; res.y = this.y / val; return res },
dot(v) { return this.x * v.x + this.y * v.y },
uDot(v, div) { return (this.x * v.x + this.y * v.y) / div },
cross(v) { return this.x * v.y - this.y * v.x },
uCross(v, div) { return (this.x * v.y - this.y * v.x) / div },
get length() { return this.lengthSqr ** 0.5 },
set length(l) { this.scale(l / this.length) },
get lengthSqr() { return this.x * this.x + this.y * this.y },
rot90CW(res = this) {
const y = this.x;
res.x = -this.y;
res.y = y;
return res;
},
};
const wV1 = new Vec2(), wV2 = new Vec2(), wV3 = new Vec2(); // pre allocated work vectors used by Line2 functions
function Line2(p1 = new Vec2(), p2 = (temp = p1, p1 = p1.p1 ? p1.p1 : p1, temp.p2 ? temp.p2 : new Vec2())) {
this.p1 = p1;
this.p2 = p2;
}
Line2.prototype = {
init(p1, p2 = (temp = p1, p1 = p1.p1, temp.p2)) { this.p1.init(p1); this.p2.init(p2) },
copy() { return new Line2(this) },
asVec(res = new Vec2()) { return this.p2.sub(this.p1, res) },
unitDistOn(u, res = new Vec2()) { return this.p2.sub(this.p1, res).scale(u).add(this.p1) },
translate(vec, res = this) {
this.p1.add(vec, res.p1);
this.p2.add(vec, res.p2);
return res;
},
translateNormal(amount, res = this) {
this.asVec(wV1).rot90CW().length = -amount;
this.translate(wV1, res);
return res;
},
unitInterceptsLine(line, res = new Vec2()) { // segments
this.asVec(wV1);
line.asVec(wV2);
const c = wV1.cross(wV2);
if (Math.isSmall(c)) { return }
wV3.init(this.p1).sub(line.p1);
res.init(wV1.uCross(wV3, c), wV2.uCross(wV3, c));
return res;
},
unitInterceptsCircle(point, radius, res = new Vec2()) {
this.asVec(wV1);
var b = -2 * this.p1.sub(point, wV2).dot(wV1);
const c = 2 * wV1.lengthSqr;
const d = (b * b - 2 * c * (wV2.lengthSqr - radius * radius)) ** 0.5
if (isNaN(d)) { return }
return res.init((b - d) / c, (b + d) / c);
},
};
/* END of file */ // Vec2 and Line2 module
/* import {vec2, Line2} from "whateverfilename.jsm" */ // Should import vec2 and line2
const POLY_SCALE = 0.5;
const ball = {
pos: new Vec2(-150,0),
delta: new Vec2(10, 10),
radius: 20,
drawPath(ctx) {
ctx.beginPath();
ctx.arc(this.pos.x, this.pos.y, this.radius, 0, Math.TAU);
ctx.stroke();
},
}
const poly = {
bRadius: 0,
lines: [],
set ballRadius(radius) {
const len = this.points.length
this.bRadius = ball.radius;
i = 0;
while (i < len) {
let line = this.lines[i];
if (line) { line.init(this.points[i], this.points[(i + 1) % len]) }
else { line = new Line2(new Vec2(this.points[i]), new Vec2(this.points[(i + 1) % len])) }
this.lines[i++] = line.translateNormal(radius);
}
this.lines.length = i;
},
points: [
new Vec2(-200, -150).scale(POLY_SCALE),
new Vec2(200, -100).scale(POLY_SCALE),
new Vec2(100, 0).scale(POLY_SCALE),
new Vec2(200, 100).scale(POLY_SCALE),
new Vec2(-200, 75).scale(POLY_SCALE),
new Vec2(-150, -50).scale(POLY_SCALE),
],
drawBallLines(ctx) {
if (this.lines.length) {
const r = this.bRadius;
ctx.beginPath();
for (const l of this.lines) {
ctx.moveTo(l.p1.x, l.p1.y);
ctx.lineTo(l.p2.x, l.p2.y);
}
for (const p of this.points) {
ctx.moveTo(p.x + r, p.y);
ctx.arc(p.x, p.y, r, 0, Math.TAU);
}
ctx.stroke()
}
},
drawPath(ctx) {
ctx.beginPath();
for (const p of this.points) { ctx.lineTo(p.x, p.y) }
ctx.closePath();
ctx.stroke();
},
movingBallIntercept(ball, res = new Vec2()) {
if (this.bRadius !== ball.radius) { this.ballRadius = ball.radius }
var i = 0, nearest = Infinity, nearestGeom, units = new Vec2();
const ballT = new Line2(ball.pos, ball.pos.add(ball.delta, new Vec2()));
for (const p of this.points) {
const res = ballT.unitInterceptsCircle(p, ball.radius, units);
if (res && units.x < nearest && Math.isUnit(units.x)) { // assumes ball started outside poly so only need first point
nearest = units.x;
nearestGeom = ballT;
}
}
for (const line of this.lines) {
const res = line.unitInterceptsLine(ballT, units);
if (res && units.x < nearest && units.isUnits()) { // first unit.x is for unit dist on line
nearest = units.x;
nearestGeom = ballT;
}
}
if (nearestGeom) { return ballT.unitDistOn(nearest, res) }
return;
},
}
const ctx = canvas.getContext("2d");
var w = canvas.width, cw = w / 2;
var h = canvas.height, ch = h / 2
requestAnimationFrame(mainLoop);
// line and point for displaying mouse interaction. point holds the result if any
const line = new Line2(ball.pos, ball.pos.add(ball.delta, new Vec2())), point = new Vec2();
function mainLoop() {
ctx.setTransform(1,0,0,1,0,0); // reset transform
if(w !== innerWidth || h !== innerHeight){
cw = (w = canvas.width = innerWidth) / 2;
ch = (h = canvas.height = innerHeight) / 2;
}else{
ctx.clearRect(0,0,w,h);
}
ctx.setTransform(1,0,0,1,cw,ch); // center to canvas
if (mouse.button) { ball.pos.init(mouse.x - cw, mouse.y - ch) }
line.p2.init(mouse.x - cw, mouse.y - ch);
line.p2.sub(line.p1, ball.delta);
ctx.lineWidth = 1;
ctx.strokeStyle = "#000"
poly.drawPath(ctx)
ctx.strokeStyle = "#F804"
poly.drawBallLines(ctx);
ctx.strokeStyle = "#F00"
ctx.beginPath();
ctx.arc(ball.pos.x, ball.pos.y, ball.radius, 0, Math.TAU);
ctx.moveTo(line.p1.x, line.p1.y);
ctx.lineTo(line.p2.x, line.p2.y);
ctx.stroke();
ctx.strokeStyle = "#00f"
ctx.lineWidth = 2;
ctx.beginPath();
if (poly.movingBallIntercept(ball, point)) {
ctx.arc(point.x, point.y, ball.radius, 0, Math.TAU);
} else {
ctx.arc(line.p2.x, line.p2.y, ball.radius, 0, Math.TAU);
}
ctx.stroke();
requestAnimationFrame(mainLoop);
}
const mouse = {x:0, y:0, button: false};
function mouseEvents(e) {
const bounds = canvas.getBoundingClientRect();
mouse.x = e.pageX - bounds.left - scrollX;
mouse.y = e.pageY - bounds.top - scrollY;
mouse.button = e.type === "mousedown" ? true : e.type === "mouseup" ? false : mouse.button;
}
["mousedown","mouseup","mousemove"].forEach(name => document.addEventListener(name,mouseEvents));#canvas {
position: absolute;
top: 0px;
left: 0px;
}<canvas id="canvas"></canvas>
Click to position ball. Move mouse to test trajectory
Vec2和Line2
为了使它更容易,向量库将有所帮助。例如,我编写了一个快速的Vec2和Line2对象(仅在示例中使用的Note函数已经过测试,注意该对象是为性能而设计的,没有经验的编码器应该避免使用这些对象,并选择更标准的向量和行库)
https://stackoverflow.com/questions/62432809
复制