更改金额N的方法数
我遇到了这个问题:
http://www.geeksforgeeks.org/dynamic-programming-set-7-coin-change/
给定一个值N,如果我们想改变N美分,并且我们有无限供应的S={ S1,S2,.,Sm)价值的硬币,我们能用多少种方法来改变?硬币的顺序并不重要。 例如,对于N=4和S= {1,2,3},有四个解:{1,1,1},{1,1,2},{2,2},{1,3}。对于N= 10和S= {2,5,3,6},有五种解:{2,2,2,2},{2,2,3},{2,2,6},{2,3,5}和{5,5}。所以输出应该是5。
我想出了解决办法:
// recurrence relation
count[N] = count[N-d] for all denomination <= N
Source code
-----------
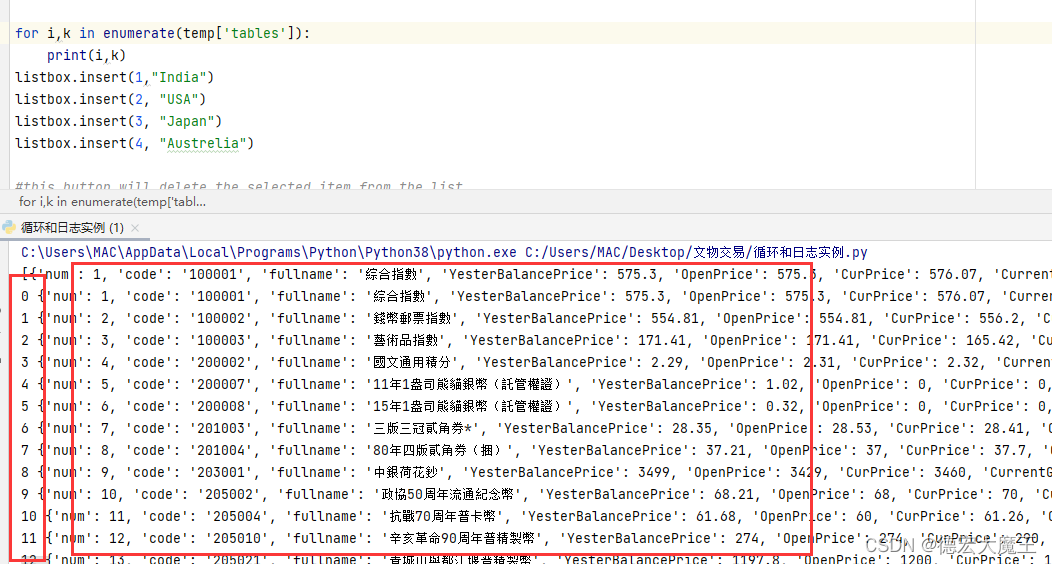
public static int numWays(int N, int[] denoms) {
if (N == 0)
return 0;
int[] ways = new int[N+1];
ways[0] = 1;
for (int i=1; i<=N; i++) {
ways[i] = 0;
for (int d : denoms) {
if (d <= i) {
ways[i] += ways[i-d];
}
}
}
return ways[N];
}但是,这会计算具有相同面额但顺序不同的重复。例如,如果面额= {1,2}和N=3,则计数具有重复条目{1,2},{2,1},{1,2}的{1,1},{1,2}。
我看到链接这里中描述的DP解决方案避免了重复。我理解递归关系是如何工作的,但是我无法理解它如何能够避免重复,而我的解决方案不是。请解释一下背后的想法。
回答 1
Stack Overflow用户
发布于 2014-09-03 22:51:21
让C(i, j)使用面额的硬币S1, ..., Sj制作总i的方法的数目。您的代码实现了以下重复(有序方式)。
C(i, m) | i < 0 = 0
| i == 0 = 1
| i > 0 = sum_{j = 1}^m C(i - Sj, m)链接代码实现了不同的重复(无序方式)。
C(i, j) | i < 0 = 0
| i == 0 = 1
| i > 0 && j <= 0 = 0
| i > 0 && j > 0 = C(i - Sj, j) + C(i, j - 1)这两种代码之间的区别是微妙的:多少只是循环是如何嵌套的。您的代码在转移到i之前添加了i + 1的所有术语,但是链接代码为每个i添加了j术语,然后为每个i添加了j + 1术语等等。因此,当链接代码考虑使用来自小计i的面额--Sj硬币的可能性时,它隐含地只考虑那些继续使用面值S1, ..., Sj硬币的解决方案,因为< code >D14的当前总数不包括使用其他硬币的可能性。
https://stackoverflow.com/questions/25657052
复制