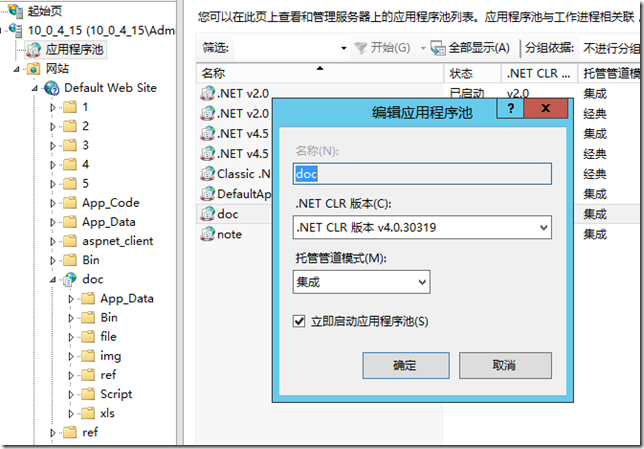
二部图中的边不同路径数
我们有一个二分图,其中集合A有n个顶点,B有n个顶点。
另外,集合A中的每个顶点都有k个边来设置B,而在集合B中的每个顶点都有k个边来设置A。
这里有一个特殊的顶点s,它有到所有顶点的边来设置A,还有一个特殊的顶点t,它对B中的所有顶点都有边。
如何证明从s到t有k个不同的路径?
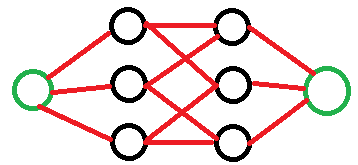
我面临的问题是,考虑到上面提到的图(减去顶点s和t),我需要证明,如果在每一轮中,我以不能从同一顶点移除超过1条边的方式删除了A到B的所有边,那么就有一种方法可以使A和B在k轮中断开。
回答 1
Stack Overflow用户
发布于 2015-11-30 01:30:56
另外,集合A中的每个顶点都有k个边来设置B,而在集合B中的每个顶点都有k个边来设置A。
=>在A中至少存在k顶点,在B中至少存在k顶点。
现在我们使用:
在B中有一个对所有顶点都有边的特殊顶点s和一个对所有顶点都有边的特殊顶点t。
(我们将称之为(II)),以表明至少必须有从k到t的k边不相交路径。
考虑以下去除过程:
- 从
s转到A中的顶点v_a。 - 从
v_a转到B中的顶点v_b。 - 从
v_b到t。 - 删除沿着这条路径的所有边缘(以确保以后不会重用它们)
注意:一个这样的删除循环正好对应于从s到t的路径。
现在:我们可以重复这个去除过程,至少k次。为什么?
因为在k-1循环之后,由于(I),必须在A中保留至少一个顶点v_a_last。这个顶点可以从s到达,因为(II)。这个顶点v_a_last必须在B中至少有一个相邻的顶点v_b_last,但我们还没有到达(v_a_last在B中有k邻居,但是到目前为止我们已经遇到最多的k-1了,因为我们只进行了k-1删除--循环)。由于到目前为止我们还没有完成v_b_last,所以从v_b_last到t的边缘必须仍然在图中。因此,在圆形k中,我们可以从s到v_a_last到v_b_last再到t,这是从s到t的k-th边缘不相交的路径。
https://stackoverflow.com/questions/33992244
复制相似问题