【计算理论】计算理论总结 ( 上下文无关文法 ) ★★
【计算理论】计算理论总结 ( 上下文无关文法 ) ★★

文章目录
参考博客 :
- 【计算理论】上下文无关语法 ( 语法组成 | 规则 | 语法 | 语法示例 | 约定的简写形式 | 语法分析树 )
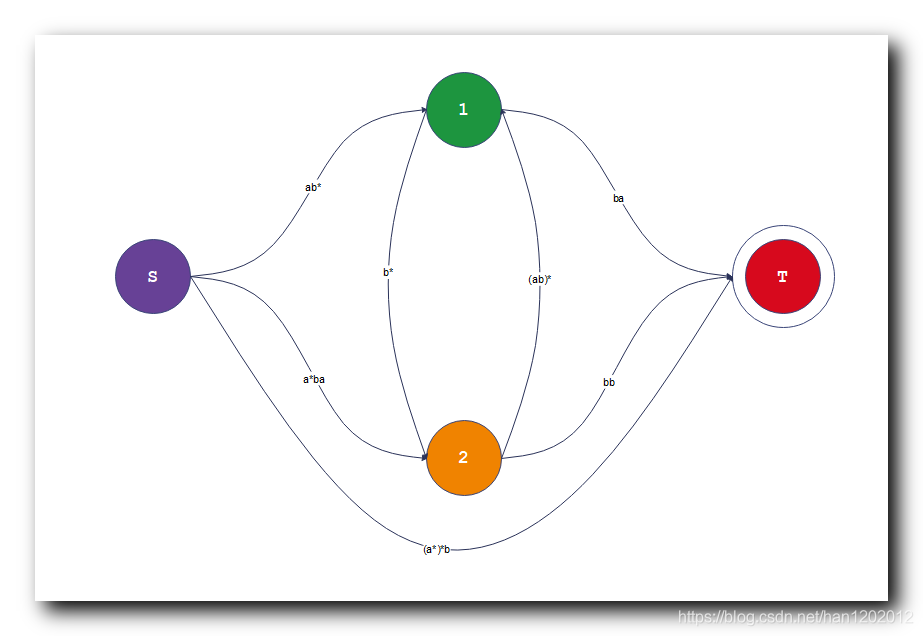
- 【计算理论】上下文无关语法 ( 代数表达式 | 代数表达式示例 | 确定性有限自动机 DFA 转为 上下文无关语法 )
- 【计算理论】上下文无关语法 CFG ( CFG 设计示例 | CFG 歧义性 | Chomsky 范式 | 上下文无关语法 转为 Chomsky 范式 )
一、上下文无关文法 ( CFG )
上下文无关语法 组成 : 由
四部分组成 ;
变量集
: 有限的变量集合 ;
终端字符集
: 有限的终端字符组成的集合 ; 相当于常量的含义 , 与变量相对 ;
规则集
: 有限的规则组成的集合 , 规则规定如何进行代换操作 , 规定 变量 , 终端字符 , 字符串变量 等 ;
开始变量
: 该变量作为开始变量 ;
规则 :
① 已知条件 : 假设
是 变量 ( 变元 ) 或 终端字符集 ( 常量 / 常元 ) ;
② 规则描述 : 规则是一个箭头 ,
,
是变元 ,
是 变元 和 常元 组成的终端字符 ;
③ 规则用法 : 在字符串中 , 根据
规则进行替换 , 只需要将
变元替换成
字符串即可 ;
④ 规则示例 :
中使用上述规则进行替换 , 将
替换成
, 替换结果是得到新字符串
;
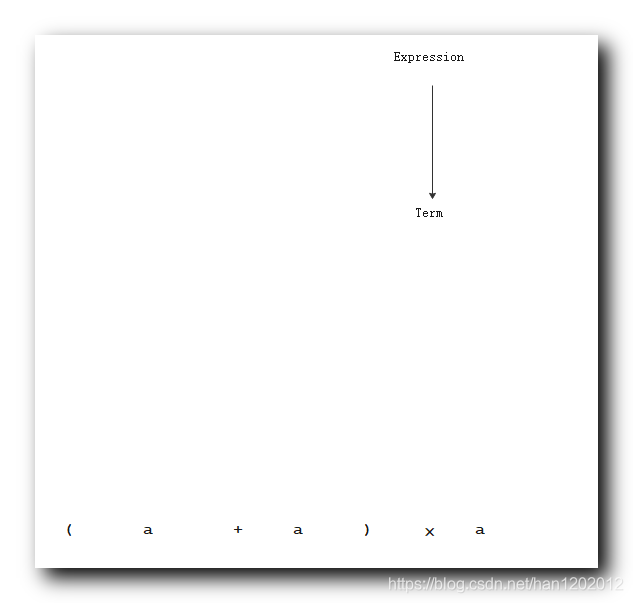
二、上下文无关文法 ( CFG ) 示例
上下文无关文法 ( CFG ) :
其组成如下 :
- 变量集
;
- 终端字符集
;
- 规则
;
- 开始变量
;
规则
描述 :
变量 可以使用
字符串替换 ;
变量 可以使用
字符串替换 ;
变量 可以使用
字符串替换 ;
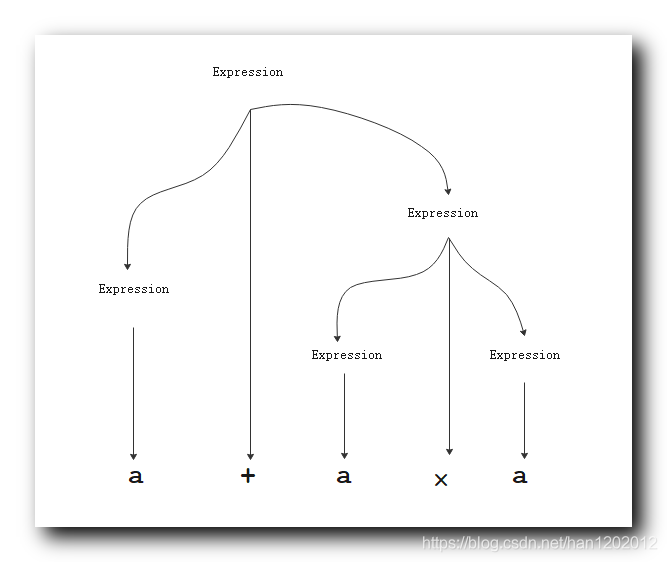
规则替换过程 : 下面的 ① ~ ⑦ 分别对应七次规则替换 ;
- ①
是开始变量 , 可以使用
替换
;
- ② 使用
替换
;
- ③ 使用
替换
;
- ④ 使用
替换第一个
;
- ⑤ 使用
替换第一个
;
- ⑥ 使用
替换
;
- ⑦ 使用
替换
;
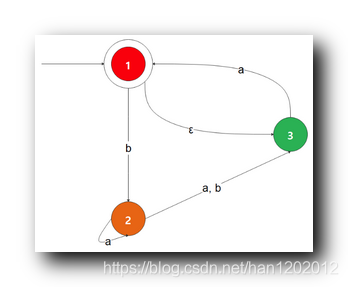
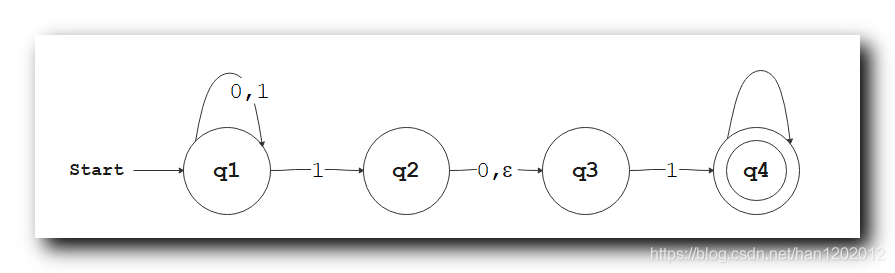
三、确定性有限自动机 DFA 转为 上下文无关语法 CFG
1 . 确定性有限自动机 ( DFA ) 转为 上下文无关语法 ( CFG ) : 将
确定性有限自动机 ( DFA ) 的指令 , 转为 对应的
上下文无关语法 ( CFG ) 规则 :
表示
状态下 , 读取字符
, 跳转到
状态 ;
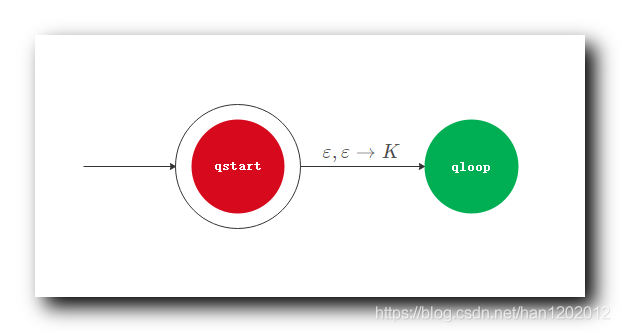
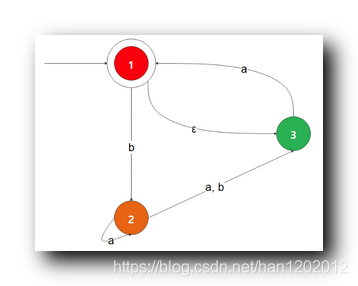
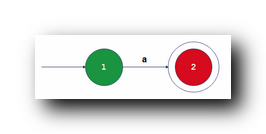
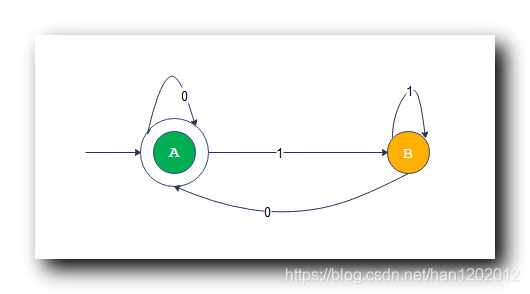
2 . 自动机的 状态跳转 转换成 规则 示例 : 下图中的 确定性有限自动机 , 开始状态
读取
字符 转化成
状态 , 表示成规则就是
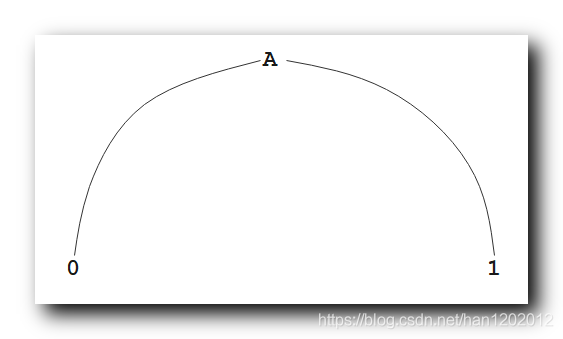
3 . 自动机的状态
读取 字符
转换成另一个状态
, 都可以转换成对应的规则
;
4 . 计算能力对比 : 上下文无关语法 的计算能力 要大于等于 自动机的计算能力 ;
- 文章目录
- 一、上下文无关文法 ( CFG )
- 二、上下文无关文法 ( CFG ) 示例
- 三、确定性有限自动机 DFA 转为 上下文无关语法 CFG

腾讯云开发者

扫码关注腾讯云开发者
领取腾讯云代金券
Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号:粤B2-20090059 深公网安备号 44030502008569
腾讯云计算(北京)有限责任公司 京ICP证150476号 | 京ICP备11018762号 | 京公网安备号11010802020287
Copyright © 2013 - 2025 Tencent Cloud.
All Rights Reserved. 腾讯云 版权所有