问四元数到达万向节锁
EN

Stack Overflow用户

提问于 2015-02-27 16:52:13

回答 2查看 8.1K关注 0票数 12

为了避免旋转时的角度锁定，我尝试切换到四元数。不知怎么的，我还在设法找到万向节锁。

我不确定是由于我实现的数学，还是设计错误，所以请指出我是否应该改变我的对象坐标的方法。

我的每个对象都持有一个X，Y，Z值，以及一个俯仰，偏航，滚动值。当我更改旋转值时，对象将根据上述信息重新计算其顶点。这一逻辑如下：

    // vertex array
    vertices[x] -= /*Offset by origin point*/;

    // Quat.'s representing rotation around xyz axes
    Quaternion q1 = Quaternion(glm::vec3(1,0,0),pitch);
    Quaternion q2 = Quaternion(glm::vec3(0,1,0),yaw); 
    Quaternion q3 = Quaternion(glm::vec3(0,0,1),roll); 

    // total rotation
    Quaternion TotalRot = ( (q3 * q2) * (q1) ); 

    // conversion of original coordinates to quaternion
    Quaternion Point1 = Quaternion(0, vertices[x].x(), vertices[x].y(), vertices[x].z()); 

    // resulting rotated point
    Quaternion Point2 = Quaternion( (TotalRot * Point1) * TotalRot.inverse() );

    // placing new point back into vertices array
    vertices[x] = QVector3D(round(Point2.v.x),round(Point2.v.y),round(Point2.v.z));
    vertices[x]+= /*Undo origin point offset*/;

"vertices[]“是对象顶点数组。上面注释掉的原点偏移量只是为了使对象围绕适当的原点旋转，因此相对于0,0,0，0，0，0，0，0，0，因为旋转发生在该点附近(对吗？)

我对我的问题有一个形象的描述，我首先偏航90度，俯仰45度，然后-90滚动，但滚动轴变得平行于俯仰轴：

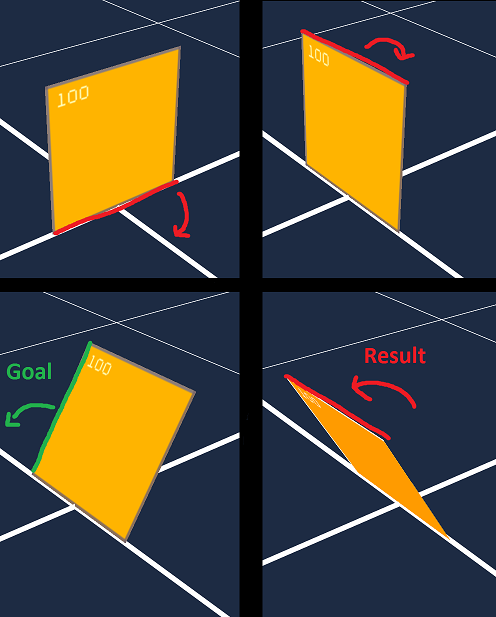
编辑：

我试着把这3轴四元数相乘，然后乘以4x4矩阵，然后乘以顶点点，但我仍然把万向节锁/到达奇点相乘！

    Quaternion q1 = (1,0,0,pitch);
    Quaternion q2 = (0,1,0,yaw);
    Quaternion q3 = (0,0,1,roll);
    Quaternion qtot = (q1*q2)*q3;
    Quaternion p1(0, vertices[x].x(), vertices[x].y(), vertices[x].z());
    QMatrix4x4 m;
    m.rotate(qtot);
    QVector4D v = m*p1;
    vertices[x] = QVector3D(v.x(),v.y(),v.z());

c++

rotation

transformation

quaternions

euler-angles

回答 2

Stack Overflow用户

发布于 2015-06-21 09:17:51

您的问题是，即使使用四元数，您仍然存储三个螺距、偏航和滚动值，而不是四元数，以表示对象的方向。

下面是使用四元数进行旋转的方法：

不是存储每个对象的X、Y、Z、螺距、偏航、滚动，而是在每个对象中存储X、Y、Z、orientation，其中orientation是从初始值(0、0、0、1)开始的四元数，意思是没有旋转。存储每个对象的俯仰、偏航和滚动容易受到奇点(万向节锁)的影响，因为当添加小的变化时，中间的一个旋转(例如，一个螺距)可能导致该对象平行于一个旋转轴(例如，偏航轴)，因此围绕该轴的下一个旋转可能失败。
然后，当对象被旋转时，确定在该帧中发生的对象的音调、偏航和滚动(假设您的输入设备以该形式提供旋转)，将其转换为四元数，然后将该四元数预乘为对象的orientation四元数。这种方法不太容易受到奇点的影响，因为预计每一帧的旋转变化都很小。
更改方向后，不要直接修改对象的X、Y和Z( verticies数组)。相反，当对象的方向发生变化时，创建一个新的旋转矩阵作为对象的世界转换矩阵的一部分(以及缩放和平移；要获得最佳结果，请将世界转换计算为translation * rotation * scaling)。
每隔几个帧，您就应该对orientation四元数进行规范化，以避免由于舍入错误而导致的方向上的不适当的更改。

票数 12

Stack Overflow用户

发布于 2015-02-27 17:28:44

如果你用一个欧拉角表示并把它转换成四元数，仅仅是为了做向量旋转，那么你仍然只是使用欧拉角。只要你在任何地方都有欧拉角，万向节锁定问题就会继续存在。你需要完全切换到四元数，如果你想要完全消除这个问题的话，永远不要在任何地方进行欧拉角表示。

这样做的基本方法是，您可以在计算的远端使用Euler角(作为原始输入或最终输出)，如果这对您更方便的话(例如，Euler角通常是一种“人类可读性”的表示)。但是，将四元数用于其他一切(您可以偶尔将其转换为旋转矩阵，因为它们对于旋转向量更有效)，并且从不对任何“坏”的旋转表示(欧拉角、轴角等)进行中间转换。“万向无锁”的四元数和旋转矩阵的好处，只有当你坚持这两个表示在你的所有计算。

因此，一方面，您有奇异表示( "gimbal锁“的正式术语是奇点)：

欧拉角(顺便说一句，有12种)；以及
轴角

在另一边，你有一个没有奇异性的表示：

四元数(更有效的内存和组合运算)；以及
旋转矩阵(更有效地将旋转应用于向量)。

每当您使用奇异表示操作(比如将几个旋转集合在一起，或移动一个旋转对象)时，您将不得不在每次计算中都担心这种奇异性。当你用奇点无关表示做同样的操作时，你就不用担心这个问题了(但是你必须担心约束，这是四元数的单位范数约束，旋转矩阵的适当正交性)。当然，任何时候，当你转换到或从一个奇异表示，你必须担心奇点。这就是为什么你只应该在你的计算的远端进行转换(当你进入或离开时)，并且在你的计算中坚持使用非奇异表示。

欧拉角的唯一好用途是为了人类的可读性，周期。

票数 8

页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持

原文链接：

https://stackoverflow.com/questions/28776788

复制

将SSRF升级为RCE

access 面向对象编程命令行工具 php html

今天我照例要和大家分享一个新的多汁漏洞。这个问题是在一个私人客户中发现的，所以我们称之为redacted.com。探索范围。在列举客户的域为子域的时候，我发现子域[docs]。我发现子域[docs]。我出来到这个子域[docs.redact.com]。寻找带外资源负载。 [docs]子域显示了一些文件和统计资料。当点击一个统计的照片时，我看到了一种奇怪的，但不是一个神奇的链接：我首先想到的是把[url]的值改为generaleg0x01.com 然后我注意到了[mimeType]参数，所以编辑

Khan安全团队

2021/01/11

2K0