简化采样多维曲线的实用算法有哪些?
提问于 2022-02-09 14:30:08
对于二维采样曲线(二维点数组),存在只保留“重要”点的Rahmer-Douglas-Peucker算法。它通过计算每个点(或样本)到连接第一个和最后一个点的直线的垂直距离来工作。如果最大距离大于一个值,则保持该点,并将该数组分成2部分。对于这两个部分,重复操作(最大垂直距离,如果大于epsilon等)。越小的感受器,就越能保持细节。
我正在尝试编写一个函数,它也可以用于高维点的更高数组。但我不知道如何定义距离。或者这真的是个好主意。我想有很多复杂和优雅的算法,适合贝齐尔和NURBS的曲线和什么的。但是否也有比较简单的呢?我不喜欢使用贝齐尔,而是简单地识别“重要的”N维点。
回答 1
Stack Overflow用户
发布于 2022-03-07 22:55:50
你可以用代数和L2范数扩展你的2D算法。假设你想要计算从点X到线段PQ的距离(其中X,P和Q被定义为N维向量)。
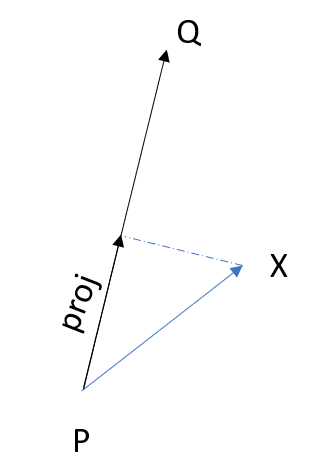
首先,可以将向量"proj“计算为:
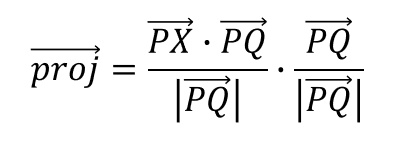
然后,距离是向量V=proj的模.
对于这个计算,你只需要向量之间的点积,这对于N维空间是很好的定义。
使用这种方法,我成功地在3D中使用了算法。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/71057623
复制













