图算法|Dijkstra算法python实现

01

—

Dijkstra算法的理论部分

关于Dijkstra算法的原理部分，请参考之前的推送：

图算法|Dijkstra最短路径算法

Dijkstra算法总结如下：

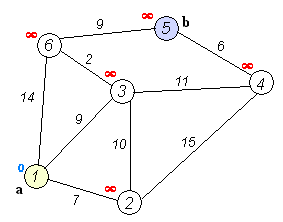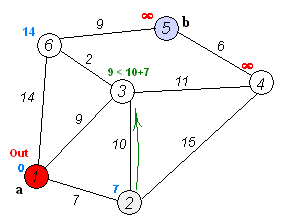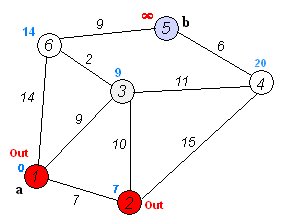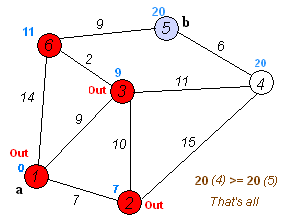
1. 此算法是计算从入度为0的起始点开始的单源最短路径算法，它能计算从源点到图中任何一点的最短路径，假定起始点为A

2. 选取一个中心点center，是S集合中的最后一个元素，注意起始点到这个点的最短距离已经计算出来，并存储在dist字典中了。

3. 因为已经求出了从A->center的最短路径，所以每次迭代只需要找出center->{有关系的节点nodei}的最短距离，如果两者的和小于dist(A->nodei)，则找到一条更短的路径。

02

—

代码实现

""" Dijkstra algorithm graphdict={"A":[("B",6),("C",3)], "B":[("C",2),("D",5)],"C":[("B",2),("D",3),("E",4)],\ "D":[("B",5),("C",3),("E",2),("F",3)],"E":[("C",4),("D",2),("F",5)],"F":[("D",3),"(E",5)]}) assert: start node must be zero in-degree """ def Dijkstra(startNode, endNode, graphdict=None): S=[startNode] V=[] for node in graphdict.keys(): if node !=startNode: V.append(node) #distance dict from startNode dist={} for node in V: dist[node]=float('Inf') while len(V)>0: center = S[-1] # get final node for S as the new center node minval = ("None",float("Inf")) for node,d in graphdict[center]: if node not in V: continue #following is the key logic.If S length is bigger than 1,need to get the final ele of S, which is the center point in current #iterator, and distance between start node and center node is startToCenterDist; d is distance between node # among out-degree for center point; dist[node] is previous distance to start node, possibly Inf or a updated value # so if startToCenterDist+d is less than dist[node], then it shows we find a shorter distance. if len(S)==1: dist[node] = d else: startToCenterDist = dist[center] if startToCenterDist + d < dist[node]: dist[node] = startToCenterDist + d #this is the method to find a new center node and # it's the minimum distance among out-degree nodes for center node if d < minval[1]: minval = (node,d) V.remove(minval[0]) S.append(minval[0]) # append node with min val return dist

03

—

测试

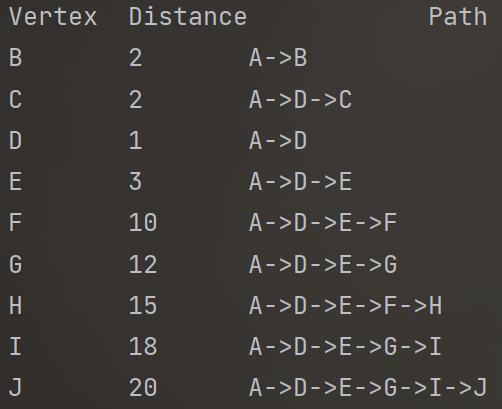
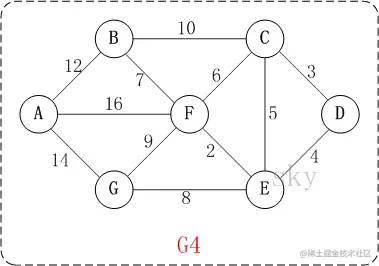
求出以上图中，从A到各个节点的最短路径：

shortestRoad = Dijkstra("A","F",graphdict={"A":[("B",6),("C",3)], "B":[("C",2),("D",5)],\

"C":[("B",2),("D",3),("E",4)],\

"D":[("B",5),("C",3),("E",2),("F",3)],\

"E":[("C",4),("D",2),("F",5)],"F":[("D",3),("E",5)]})

mystr = "shortest distance from A begins to "

for key,shortest in shortestRoad.items():

print(mystr+ str(key) +" is: " + str(shortest) )

打印结果如下：

shortest distance from A begins to B is: 5 shortest distance from A begins to C is: 3 shortest distance from A begins to D is: 6 shortest distance from A begins to E is: 7 shortest distance from A begins to F is: 9