问Dijkstra与MST的关系

EN

然而，

是否保证在一个无向、加权、连通的图中必须存在一个节点，如果我们选择它作为源并应用Dijkstra的算法，它将为该图生成一个MST？

不，Dijkstra的算法最小化了从单个节点到所有其他节点的路径权重。最小生成树最小化将所有节点连接在一起所需的权重之和。没有理由期望这些不同的需求会导致相同的解决方案。

考虑一个完整的图，其中任意两个边的权重之和超过了任何单个边的权重。这迫使Dijkstra始终选择直接连接作为两个节点之间的最短路径。然后，如果图中的最低权边并非都来自一个节点，则最小生成树将不与Dijkstra生成的任何树相同。

下面是一个例子：

​

​

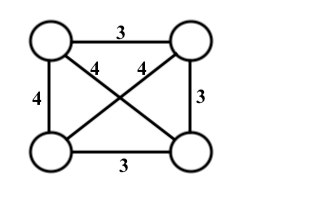
最小生成树由三条边组成，权重为3(总权重9)。Dijkstra算法返回的树将是直接连接到源节点的三条边(总权重10或11)。