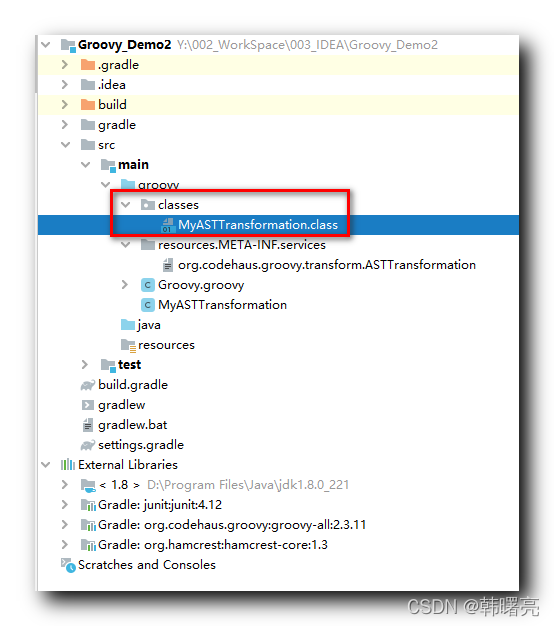
hmmlearn:如何在时间T+1中得到隐藏状态概率的预测，给出一个完整的观测序列1:T
hmmlearn:如何在时间T+1中得到隐藏状态概率的预测，给出一个完整的观测序列1:T
提问于 2017-06-03 19:15:24
我使用hmmlearn的GaussianHMM来训练带有高斯观测的隐马尔可夫模型。每个隐藏状态k都有相应的高斯参数: mu_k、Sigma_k。
在对模型进行培训之后，我想计算以下数量：
P(z_{T+1} =j+ x_{1:T})，
其中j= 1，2，.K，K是隐藏态的个数。
上述概率基本上是一步一步的隐藏状态概率，给定一个完整的观测序列: x_1，x_2，.，x_T，其中x_i，i=1，.，T被用来训练HMM模型。
我读了文档，但是找不到一个函数来计算这个概率。有什么解决办法吗？
回答 2
Stack Overflow用户
回答已采纳
发布于 2017-07-25 06:59:41
您正在寻找的概率只是过渡矩阵中的一行。转换矩阵的第n行给出了在时间上转换到每个状态的概率，t+1知道系统在时间上是t。
为了知道系统处于什么状态，t给出了一个x_1,...,x_t序列，可以使用hmmlearn中predict方法的默认设置维特比算法。
model = hmm.GaussianHMM(n_components=3, covariance_type="full", n_iter=100) # Viterbi is set by default as the 'algorithm' optional parameter.
model.fit(data)
state_sequence = model.predict(data)
prob_next_step = model.transmat_[state_sequence[-1], :]我建议您仔细看看这个文档，它显示了具体的使用示例。
Stack Overflow用户
发布于 2018-07-12 23:23:49
一旦对an HMM model进行了培训，您就可以获得给定1:t观测X的t+1状态如下：
import numpy as np
from sklearn.utils import check_random_state
sates = model.predict(X)
transmat_cdf = np.cumsum(model.transmat_, axis=1)
random_sate = check_random_state(model.random_state)
next_state = (transmat_cdf[states[-1]] > random_state.rand()).argmax()t+1状态根据t状态和transmat_生成。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接：
https://stackoverflow.com/questions/44350447
复制相关文章
安装RabbitMQ编译erlang时，checking for c compiler default output file name... configure:error:C compiler c
点击加载更多
相似问题
资源池中的系统内存不足，无法在Server 2008中执行SQL脚本
SQL缓冲区页面快速增加SQL Server内存使用量
缓冲池中没有可用的空闲缓冲区
SQL Server -高缓冲时间
SQL Server中的写缓冲
添加站长 进交流群
领取专属 10元无门槛券
AI混元助手 在线答疑
关注 腾讯云开发者公众号
洞察 腾讯核心技术
剖析业界实践案例
腾讯云开发者
