R语言进阶之因子分析
R语言进阶之因子分析
在介绍因子分析之前,我想和大家解释一下主成分分析和因子分析的区别:
(1)主成分分析主要是对原始变量进行线性组合,不涉及模型与假设,而因子分析则需要构造一个因子模型并伴随相关假设;
(2)主成分分析的解是唯一确定的,而因子分析的解往往不唯一;
(3)最后,因子分析对结果的解释效果往往比主成分分析更好,更具有现实意义。
我们可以使用R语言的内置函数factanal()来进行因子分析,该函数使用的是极大似然估计法,我们使用mtcars数据集作为示例数据。
1. 探索性因子分析
mydata <- mtcars
# 极大似然因子分析
# 提取2个因子,使用最大方差法旋转
fit <- factanal(mydata, 3, rotation="varimax") # 第2个参数是提取的因子个数
print(fit, digits=2, cutoff=0.3, sort=TRUE) # 输出结果
从上面的结果可以看到,Loadings部分第1个因子主要反映的是前7项变量的共同特征,而第2个因子主要反映后5项变量的特征,并且这两个因子的累计方差贡献率达到72%。另外,这三个因子是否能充分解释这些变量特征的假设检验结果P值为0.205 (大于0.05),说明这三个因子足以解释这些变量了。
load <- fit$loadings[,1:2]
plot(load,type="n") # 绘图
text(load,labels=names(mydata),cex=1) # 添加变量名
从上图可以看出,不同的变量可以用这两个因子进行区分。
另外,“psych”包的fa()函数也提供了各种相关的因子分析方法,使用起来十分方便,包括主轴因子分析(principal axis factor analysis):
# 主轴因子分析
library(psych)
r <- corr.test(mydata)$r # 提取各个变量之间的相关系数矩阵
fit2 <- fa(r, nfactors=3, rotate="varimax",fm="pa") # 指定因子个数,旋转方法和计算方法
fit2 # 输出结果
上图的结果解释和之前的一样,这里就不赘述了!
2. 确定要提取的因子数目
探索性因子分析最关键的就是确定提取的因子个数,这里R包“nFactors”就提供了一套函数用于辅助确定因子个数:
# 确定应提取的因子个数
library(nFactors)
ev <- eigen(cor(mydata)) # 获取特征值
ap <- parallel(subject=nrow(mydata),var=ncol(mydata),
rep=100,cent=.05) # subject指样本个数,var是指变量个数
nS <- nScree(x=ev$values, aparallel=ap$eigen$qevpea) # 确定探索性因子分析中应保留的因子
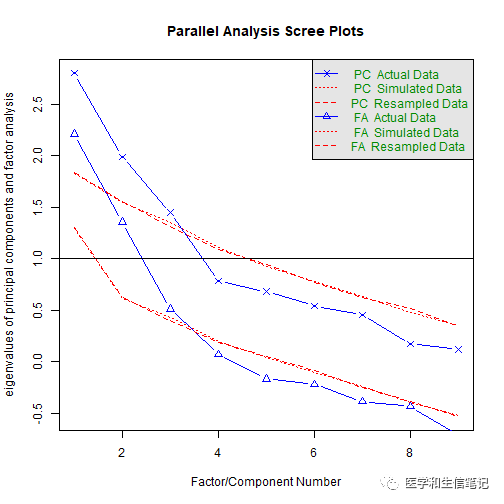
plotnScree(nS) # 绘制碎石图
该图的横坐标反映的的是各个因子,纵坐标对应各个因子的特征值,可以看出从第4个因子开始,它们的特征值几乎就没有变化了。所以从上图不难看出,选择三个因子是最佳的。
关于探索性因子分析的内容就讲解到这里,感兴趣的朋友可以学习一下验证性因子分析的相关内容。
- 在介绍因子分析之前,我想和大家解释一下主成分分析和因子分析的区别:
- (1)主成分分析主要是对原始变量进行线性组合,不涉及模型与假设,而因子分析则需要构造一个因子模型并伴随相关假设;
- (2)主成分分析的解是唯一确定的,而因子分析的解往往不唯一;
- (3)最后,因子分析对结果的解释效果往往比主成分分析更好,更具有现实意义。
- 1. 探索性因子分析
- 上图的结果解释和之前的一样,这里就不赘述了!
- 2. 确定要提取的因子数目

腾讯云开发者

扫码关注腾讯云开发者
领取腾讯云代金券
Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号:粤B2-20090059 深公网安备号 44030502008569
腾讯云计算(北京)有限责任公司 京ICP证150476号 | 京ICP备11018762号 | 京公网安备号11010802020287
Copyright © 2013 - 2025 Tencent Cloud.
All Rights Reserved. 腾讯云 版权所有