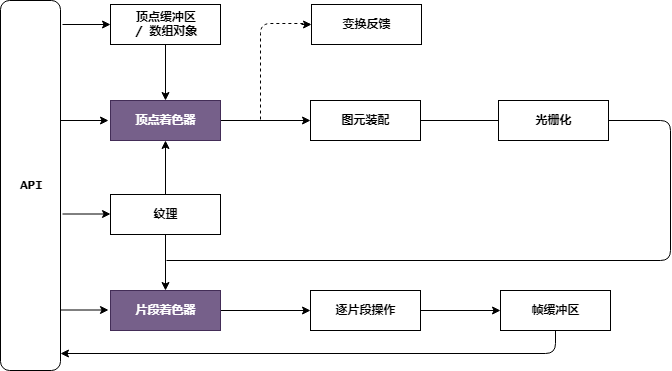
OpenGL ES 着色语言
OpenGL ES 着色语言
转载请以链接形式标明出处: 本文出自:103style的博客
OpenGL ES 3.0学习汇总
目录
- 变量和变量类型
- 向量和矩阵的构造及选择
- 常量
- 结构和数组
- 运算符、控制流和函数
- 输入/输出变量、统一变量、统一变量块和布局限定符
- 预处理器和指令
- 统一变量和插值器打包
- 精度限定符和不变性
着色器语言规范
OpenGL ES 3.0的顶点着色器和片段着色器第一行总是声明着色器版本。
# version 300 es
没有声明版本的表示用的 OpenGL ES着色语言的1.0版本,对应OpenGL ES 2.0。
变量和变量类型
变量分类 | 类型 | 描述 |
|---|---|---|
标量 | float, int, uint, bool | 用于浮点、整数、无符号整数和布尔值的基本标量的数据类型 |
浮点向量 | float, vec2, vec3, vec4 | 有1、2、3、4个分量的基于浮点的向量类型 |
整数向量 | int, ivec2, ivec3, ivec4 | 有1、2、3、4个分量的基于整数的向量类型 |
无符号整数向量 | uint, uivec2, uivec3, uivec4 | 有1、2、3、4个分量的基于无符号整数的向量类型 |
布尔向量 | bool, bvec2, bvec3, bvec4 | 有1、2、3、4个分量的基于布尔的向量类型 |
矩阵 | mat2(或 mat2 * 2),mat2 * 3 , mat2 * 4, mat3 * 2, mat3(或 mat3 * 3), mat3 * 4, mat4 * 2, mat4 * 3, mat4(或者 mat4 * 4) | 2 * 2, 3 * 2, 3 * 3, 3 * 4, 4 * 2, 4 * 3 , 4 * 4的基于浮点的矩阵 |
变量构造器
- 初始化和转换标量
float myFloat = 1.0;
float myFloat = 1; //ERROR: invalid type conversion.
bool myBool = true;
int myInt = 0;
int myInt2 = 0.0; //ERROR: invalid type conversion.
myFloat = float(myBool); //Convert from bool → float
myFloat = float(myInt); //Convert form int → float
myBool = bool(myInt); //Convert form init → bool- 初始化和转换向量
- 如果只为向量构造器提供一个标量参数,则该值用于设置向量的所有值
- 如果提供多个标量或者向量参数,则从左至右使用者写参数设置。如果提供多个标量参数,则参数中必须有至少和参数中一样多的分量。
vec4 myVec4 = vec4(1.0); //myVec4 = {1.0, 1.0, 1.0, 1.0}
vec3 myVec3 = vec3(1.0, 0.0, 0.5); //myVec3 = {1.0, 0.0, 0.5}
vec3 temp = myVec3; //temp = myVec3 = {1.0, 0.0, 0.5}
vec2 myVec2 = vec2(myVec3); //myVec2 = {myVec3.x, myVec3.y}
vec4 myVec4 = vec4(myVec2, temp); //myVec4 = {myVec2.x, myVec2.y, temp.x, temp.y}- 矩阵的构造
- 如果矩阵构造器只提供 一个标量参数,则该值被赋值到 矩阵的对角线 上。
- 矩阵可以从多个向量参数构造,e.g. mat2 可以从两个vec2构造
- 矩阵可以从多个标量参数构造——每个参数代表矩阵中的一个值,从左到右使用。
只要提供足够多的分量,矩阵可以从任何标量和向量组合构造。 矩阵以 列优先 顺序存储。
mat3 myMat3 = mat3(1.0, 0.0, 0.0, //first column
0.0, 1.0, 0.0, //second column
0.0, 1.0, 1.0);//third column对应矩阵:
| 1.0 0.0 0.0 |
| 0.0 1.0 1.0 |
| 0.0 0.0 1.0 |向量和矩阵分量
向量的单独分量两种访问方式:
使用 . 运算符。 可以通过{x, y, z, w}、{r, g, b, a}、{s, t, p, q} 某一种组合访问。
vec3 myVec3 = vec(0.0, 1.0, 2.0); // myVec3 = {0.0, 1.0, 2.0}
vec3 temp;
temp = myVec3.xyz; // temp = {0.0, 1.0, 2.0}
temp = myVec3.xxx; // temp = {0.0, 0.0, 0.0}
temp = myVec3.zyx; // temp = {2.0, 1.0, 0.0}通过数组下标。 下标从0开始。 矩阵可以看作一个二维数组
mat4 myMat4 = mat4(1.0);
vec4 col0 = myMat4[0]; //col0 = {1.0 , 0.0, 0.0, 1.0}
float m1_1 = myMat4[1][1]; // m1_1 = 1.0;
float m2_2 = myMat4[2].z; // m2_2 = 1.0;常量
可以将任何基本类型声明为常数变量。常数变量是着色器中不变的值。 用 const 限定符修饰。
常量必须在 声明时 初始化。
常量是只读的。和 C 和 C++ 中一样。
类似 java 中 final String s = "t";
结构
语法:
struct testStruct
{
vec4 color;
float start;
float end;
} testVar;结构可以构造器初始化,参数类型必须是一 一对应的。
testVar = testStruct(vec4(0.0, 1.0, 0.0, 0.0), //color
0.5, //start
2.0); //end访问方式:
vec4 color = testVar.color;
float start = testVar.start;
float end = testVar.end;数组
数组语法和C语言很相似。数组构造器中的参数数量必须等于数组的大小。
float floatArr[4];
vec4 vecArr[2];
float a[4] = float[]{1.0, 2.0, 3.0, 4.0};
float b[4] = float[4]{1.0, 2.0, 3.0, 4.0};
vec2 c[2] = vec2[2]{vec2(1.0), vec2(1.0)};运算符
和 C、Java 类似。
运算符类型 | D描述 |
|---|---|
+、-、 *、 /、% | 加、减、乘、除、取模 |
++, – | 递增 递减 |
=、 +=,-=,*=,/= | 赋值 以及 算术 赋值 |
==,!=,<,>,<=,>= | 比较运算符 |
&&,||,^^ | 逻辑与,逻辑或,逻辑异或 |
<<,>> | 移位 |
&,^,| | 按位 与,异或,或 |
?: | 选择 |
’ | 序列 |
函数
函数的声明方法和 C语言中相同。
OpenGL ES着色语言函数 和 C语言函数 的区别在于 函数的传递方法 以及 着色语言函数不能递归 不能递归的原因是某些函数通过把函数代码真正的内嵌到为GPU生成的最终程序来实施函数调用,着色语言有意的构造为允许这种内嵌实现,以支持没有堆栈的GPU。
着色语言提供特殊的限定符,定义函数是否可以修改可变参数。
限定符 | 描述 |
|---|---|
in | 默认限定符,指定参数按值传送,函数不能修改 |
inout | 变量按照引用传入函数 ,如果值被修改,将在函数退出后变化 |
out | 表示变量的值不被传入函数,但是在函数返回是将被修改 |
用法:
vec4 myFunc(inout flaot myFloat,
out vec4 myVec4,
mat4 myMat4);
vec4 diffuse(vec3 normal, vec3 light, vec4 baseColor)
{
return baseColor * dot(normal, light);
}内建函数
着色器语言最强大的功能之一。 类似 Java 提供的 jdk。
控制流语句
简单的 if-then-else、while、do-while 完全 和 C语言语法相同。
if(color.a < 0.25)
{
color *= color.a;
}
else
{
color = vec4(0.0);
}####统一变量
- 统一变量储存应用成簇通过API传入着色器的只读值, 用
uniform限定符修饰。 - 统一变量的命名空间在 顶点着色器 和 片段着色器 中都是共享的。如果两者中都声明了一个统一变量,那么两个声明必须匹配。
- 统一变量通常保存在硬件中,这块区域被称作 “常量存储”,是硬件为储存常量值而分配的特殊空间,大小一般是固定的,可以通过读取内建变量
gl_MaxVertexUniformVectors和gl_MaxFragmentUniformVectors值来确定。OpenGL ES 3.0实现必须提供至少256个顶点统一变量和224个片段统一变量。
####统一变量块
#version 300 es
uniform TransformBlock
{
mat4 matViewProj;
mat3 matNormal;
mat3 matTexGen;
};
layout(location = 0) in vec4 a_position;
void main()
{
gl_position = matViewProj * a_position;
}一些可选的布局限定符可用于指定统一变量块得的统一缓冲区对象在内存中的布局方式。
layout(shared, column_major) uniform;//default if not
layout(packed, row_major) uniform; //specified统一变量块布局限定符:
限定符 | 描述 |
|---|---|
shared | 指定多个着色器或者多个程序中统一变量块的内存布局相同。要使用这个限定符,不同定义的row_major/column_major值必须相等。覆盖 std140 和 packed(默认) |
packed | 制定编译器可以优化统一变量块的内存布局。使用这个是必须查询偏移位置,而且不能在 顶点/片段着色器 或者 程序间共享,覆盖std140 和 shared |
std140 | 制定统一变量块的布局基于OpenGL ES 3.0规范的 “标准统一变量块” 中定义的一组标准规则。覆盖shared和packed |
row_major | 矩阵在内存中以行优先布局 |
column_major | 矩阵在内存中以列优先布局(默认) |
顶点和片段着色器输入/输出
输入 用 in 关键字 指定, 输出 用 out 关键字 指定。
顶点和片段着色器 输入变量不能有布局限定符。OpenGL ES实现自动选择位置。
OpenGL ES 着色语言中另一个特殊变量类型是 顶点输入变量。 顶点输入变量指定顶点着色器中每个顶点的输入,用 in关键字指定。它们通常存储位置、法线、纹理坐标和颜色这样的数据。
和统一变量一样,底层硬件也会限制 可输入顶点着色器的属性变量、顶点着色器输出 、片段着色器输入 的数量,
- 可输入顶点着色器的属性变量最大属性数量由
gl_MaxVertexAttribs给出。 OpenGL ES 3.0实现可支持的最小属性为16个。如果想要编写保证能在任何OpenGL ES 3.0实现上运行的着色器。则属性限制为不多于16个。 - 顶点着色器输出由内建变量
gl_MaxVertexOutputVectors给出。OpenGL ES 3.0实现可支持的最小顶点输出向量数为16个。 - 片段着色器输入由
gl_MaxFragmentInputVectors给出。OpenGL ES 3.0实现可支持的最小片段输入向量数为15个。
//Vertex shader
#version 300 es
uniform mat4 u_matVireProjection;
//Vertex shader inputs
layout(location = 0) in vec4 a_postion;
layout(location = 1) in vec3 a_color;
//Vertex shader output
out vec3 v_color;
void main(void)
{
gl_Postion = u_matViewProjrction * a_position;
c_color = a_color;
}
//Fragment shader
#verison 300 es
precision mediump float;
//Input from vertex shader
in vec3 v_color;
//Output of fragment shader
layout(location = 0) out vec4 o_fragColor;
void main()
{
o_fragColor = vec4(v_color, 1.0);
}插值限定符
默认的插值行为是 执行平滑着色。
以下是明确的请求平滑着色代码。
// Vertex shader
smooth out vec3 v_color;
//Fragment shader
smooth in vec3 v_color;插值限定符 | 描述 |
|---|---|
smooth 平滑着色 | 在图元中进行线性插值 |
flat 平面着色 | 在图元中没有进行插值,而是将顶点是为驱动定点,该顶点的值被用于图元中的所有片段 |
最后,可以用centroid 关键字 在插值器中添加另一个限定度——质心采样。
smooth centroid out vec3 v_color;
//Fragment shader
smooth centroid in vec3 v_color;预处理器和指令
可以使用以下指令定义宏和条件测试:
#define
#undef
#if
#ifdef
#ifndef
#else
#elif
#endif宏不能定义为带有参数。 以下的宏是预先定义的。
_LINE_ // replaced with the current line number in a shader
_FILE_ // always 0 in OpenGL ES 3.0
_VERSION_ // the OpenGL ES shading language version
GL_ES // this will be defined for ES shaders to a values of 1指令:
指令名 | 描述 |
|---|---|
#error | 将会导致在着色器编译时出现编译错误,并在信息日志中放入对应的消息。 |
#pragma | 用于编译器指定特定与实现的指令。 |
#extension | 用于启用 和 设置扩展的行为。 |
以下代码展示了#extension的一般格式:
//set behavior for an extension
# extension extension_name : behavior
//set behavior for all extensions
#extension all : behavior扩展行为 | 描述 |
|---|---|
require | 扩展是必需的,因此预处理器在扩展不受支持是将抛出错误,如果指定了all,将总是抛出错误 |
enable | 扩展被启用,因此拓展不受支持是预处理器将抛出警告。如果扩展被启用,该语言将被处理,如果指定了all,将总是抛出错误 |
warn | 对于拓展的任何使用均提出警告,除非这种使用是另一个已经启用用的扩展所必循的,如果指定了all,则在使用扩展时都将抛出警告 |
disable | 扩展被禁用,因此使用拓展将抛出错误,如果制定了all(默认),则不启用任何拓展 |
e.q. 假定你希望预处理器在NVIDIA阴影采样器立方体扩展不受支持时产生警告,可以添加以下语句:
#extension GL_NV_shadow_samplers_cube : enable统一变量和插值器打包
着色器的各种 变量声明如何映射到硬件上的可用物理空间呢? 在OpenGL ES 3.0中,这个问题通过打包规则处理,该规则定义插值器和统一变量映射到物理存储空间的方式。 打包规则基于物理存储空间被组织为一个 每个存储位置4列(每个向量分量一列)和 1 行的网格 的概念。 打包规则寻求打包变量,使生成代码复杂度保持不变。换言之,打包规则不进行重新排序操作。
下面展示了如何打包的例子:
uniform mat3 m;
uniform float f[6];
uniform vec3 v;如果不进行打包: 矩阵 m 将占据 3 行,数组 f 占据 6 行,向量v 占据1 行,一共10行才能存储这些变量。 如下所示:
位置 | X | Y | Z | W |
|---|---|---|---|---|
0 | m[0].x | m[0].y | m[0].z | - |
1 | m[1].x | m[1].y | m[1].z | - |
2 | m[2].x | m[2].y | m[2].z | - |
3 | f[0] | - | - | - |
4 | f[1] | - | - | - |
5 | f[2] | - | - | - |
6 | f[3] | - | - | - |
7 | f[4] | - | - | - |
8 | f[5] | - | - | - |
9 | v.x | v.y | v,z | - |
打包之后: 则只需使用 6 个物理常量位置。
位置 | X | Y | Z | W |
|---|---|---|---|---|
0 | m[0].x | m[0].y | m[0].z | f[0] |
1 | m[1].x | m[1].y | m[1].z | f[1] |
2 | m[2].x | m[2].y | m[2].z | f[2] |
3 | v.x | v.y | v,z | f[3] |
4 | - | - | - | f[4] |
5 | - | - | - | f[5] |
精度限定符
分为 低、中、高 三个精度,在较低的精度上,有些OpenGL ES实现在运行着色器时可能更快当然这是以精度为代价的。没有使用正确的精度可能会造成伪像。
FP范围 | FP幅值范围 | FP精度 | 整数范围 有符号 | 整数范围 无符号 | |
|---|---|---|---|---|---|
highp | (2-126,2127) | 0.0, (2-126,2127) | 2-24 | (2-31,231-1) | (0,232-1) |
mediump | (2-14,214) | (2-14,214) | 2-10 | (2-15,215-1) | (0,216-1) |
lowp | (-2,2) | (2-8,2) | 2-8 | (2-7,27-1) | (0,28-1) |
除了精度限定符,还可以使用默认精度。默认精度符在着色器的开头用如下语法指定。
precision highp flaost;
precision mediumo int;在 顶点着色器 中,如果没有指定,int 和 float 默认为 highp。
在 片段着色器 中,浮点值 没有默认的精度值。 每个片段着色器必须声明一个默认的 float 精度。
不变性
OpengGL ES着色语言中引入 invariant 关键字可以用于任何可变的顶点着色器输出。
引入不变性的原因 :因为着色器需要编译,编译会导致指令重新排序的优化。 这种指令意味着两个着色器之间的等价计算不能保证产生完全相同的结果。
invariant 关键字可以用于 变量声明,或者 用于已经声明的变量。
invariant gl_Position;
invariant texCoord;一旦某个输出变量声明了不变性。编译器便保证相同的计算和着色器输出条件下结果相同。
警告:因为编译器需要保证不变性,所以可能限制他所做的优化。因此,只有在必要时才使用invariant关键字,否则可能导致性能下降。
腾讯云开发者

扫码关注腾讯云开发者
领取腾讯云代金券
Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号:粤B2-20090059 深公网安备号 44030502008569
腾讯云计算(北京)有限责任公司 京ICP证150476号 | 京ICP备11018762号 | 京公网安备号11010802020287
Copyright © 2013 - 2025 Tencent Cloud.
All Rights Reserved. 腾讯云 版权所有