用可视化技术打开AI模型的黑箱
原创用可视化技术打开AI模型的黑箱

在人工智能技术快速发展的今天,一个令人困扰的问题始终萦绕在开发者心头:我们如何理解那些动辄数百万参数的复杂模型?当深度学习模型在图像识别任务中将猫误判为狗时,当推荐系统意外推送不相关商品时,当医疗诊断AI给出矛盾结论时,数据可视化技术就像一把打开黑箱的金钥匙,让我们得以窥见模型决策的奥秘。本文将带你走进JupyterLab的魔法世界,用Matplotlib和Seaborn这两柄利器,揭开AI模型的神秘面纱。
一、可视化
在AI开发领域流传着一句箴言:"如果不能用图表解释,说明你还没真正理解。"数据可视化之于机器学习,就像显微镜之于生物学,它不仅将抽象的数字转化为直观图形,更能帮助我们发现数据中的隐藏规律。
想象你正在训练一个肺炎诊断模型,看着控制台里跳动的准确率数字,80%、82%、85%...这些数字本身无法告诉你:模型是否在死记硬背?是否对某些病例存在系统性误判?此时,一组精心设计的可视化图表,就像给模型装上了X光机,让我们能透视学习过程的全貌。
二、搭建你的可视化实验室
工欲善其事,必先利其器。我们在JupyterLab这个"数字实验室"中搭建工作环境:
# 科学家的工具箱
import matplotlib.pyplot as plt # 绘图界的瑞士军刀
import seaborn as sns # 统计可视化的美学大师
import pandas as pd # 数据整理的魔法书
import numpy as np # 数值计算的基石
# 设置画布风格
sns.set(style="whitegrid", # 白色网格背景
palette="husl", # 彩虹色系
font_scale=1.3) # 放大字体
# 魔法指令让图表内嵌显示
%matplotlib inline这个初始化过程就像实验室的器材准备:Matplotlib提供基础绘图工具,Seaborn带来更美观的统计图表,Pandas负责数据整理,Numpy处理数值计算。通过Seaborn的样式设置,我们统一了视觉风格,确保所有图表具有专业统一的呈现效果。
三、训练过程的"心电图"监测
3.1 损失曲线
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
learning_history = {
'epochs': range(1, 11),
'train_loss': [2.1, 1.5, 1.2, 0.9, 0.7, 0.6, 0.5, 0.4, 0.3, 0.25],
'val_loss': [2.0, 1.8, 1.6, 1.5, 1.4, 1.4, 1.4, 1.45, 1.5, 1.55]
}
# Convert range to list for epochs
epochs = list(learning_history['epochs'])
plt.figure(figsize=(10, 6))
sns.lineplot(x='epochs', y='value', hue='variable',
data=pd.DataFrame({
'epochs': epochs * 2,
'value': learning_history['train_loss'] + learning_history['val_loss'],
'variable': ['训练损失'] * 10 + ['验证损失'] * 10
}))
plt.title('模型损失曲线')
plt.xlabel('训练轮次')
plt.ylabel('损失值')
plt.annotate('出现过拟合!', xy=(7, 1.4), xytext=(5, 1.8),
arrowprops=dict(facecolor='red', shrink=0.05))
plt.show()
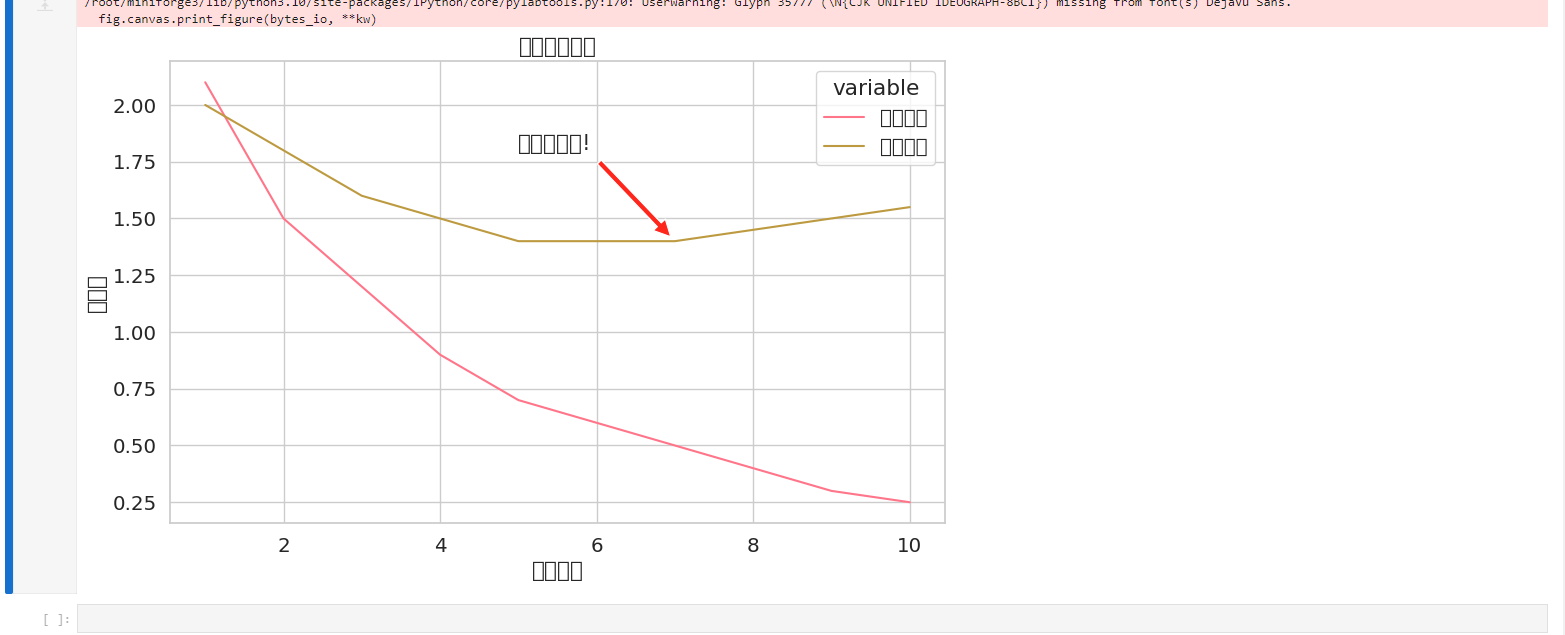
这段代码生成的曲线图就像模型的心电图:蓝色训练损失线持续下降,说明模型在学习;红色验证损失线在第七轮后突然上扬,犹如心跳异常,提示模型开始死记硬背训练数据(过拟合)。这时我们就需要像医生处理心电图异常一样,采取早停(Early Stopping)或正则化措施。
3.2 准确率曲线
plt.figure(figsize=(10, 6))
ax = sns.lineplot(x='epochs', y='accuracy', data=pd.DataFrame({
'epochs': learning_history['epochs'],
'accuracy': [0.65, 0.72, 0.78, 0.82, 0.85, 0.87, 0.89, 0.91, 0.93, 0.95]
}))
ax.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f"{x:.0%}")) # 转换为百分比
plt.axhline(y=0.9, color='green', linestyle='--', label='目标阈值')
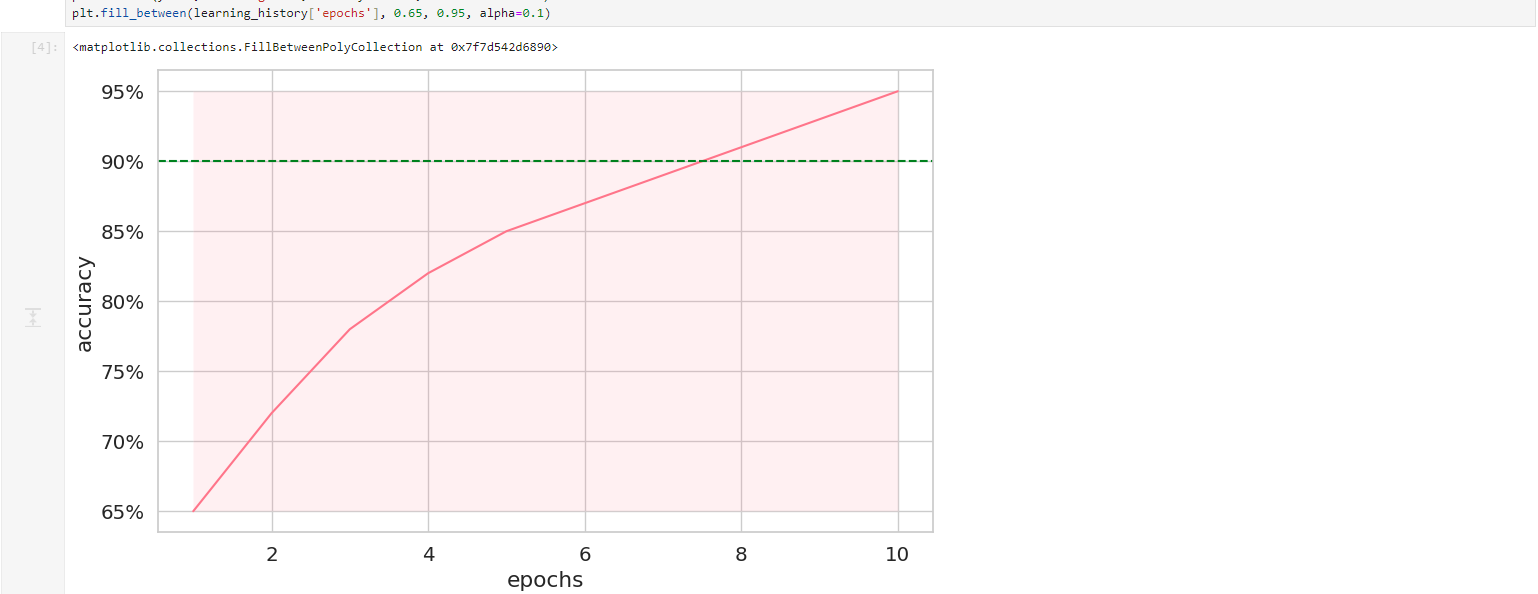
plt.fill_between(learning_history['epochs'], 0.65, 0.95, alpha=0.1)这个准确率曲线图配以目标阈值线,清晰展示了模型何时突破业务要求的性能门槛(90%)。渐变填充区域则形象地描绘出学习过程的波动范围,帮助我们判断模型表现是否稳定。
四、模型体检
4.1 混淆矩阵
# 生成医疗诊断案例的混淆矩阵
diagnosis_labels = ['肺炎', '肺结核', '健康']
confusion = np.array([[85, 5, 10],
[8, 72, 20],
[2, 3, 95]])
plt.figure(figsize=(10, 8))
sns.heatmap(confusion, annot=True, fmt='d', cmap='YlGnBu',
xticklabels=diagnosis_labels,
yticklabels=diagnosis_labels)
plt.title('呼吸系统疾病诊断混淆矩阵')
plt.xlabel('预测诊断')
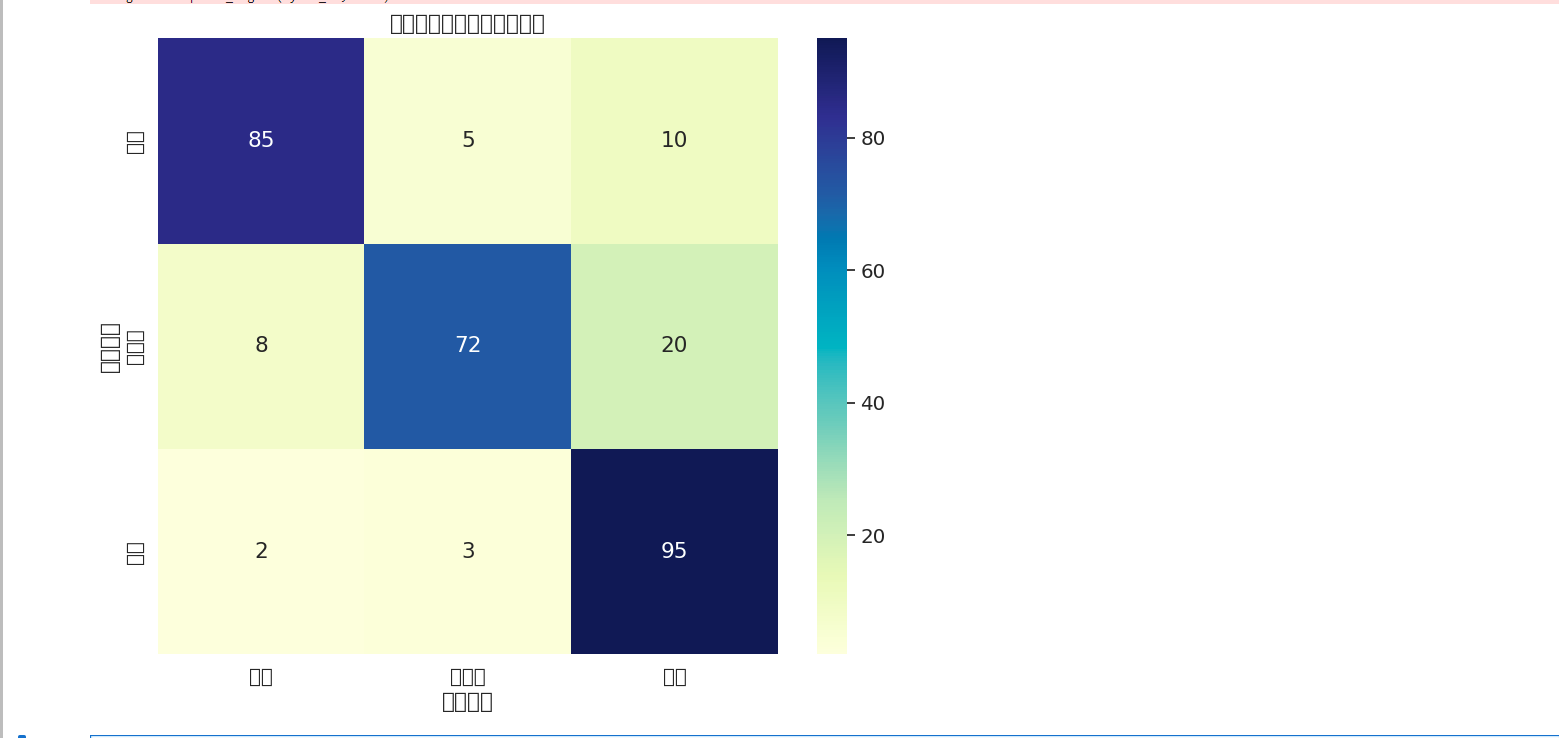
plt.ylabel('真实病情')这个医疗诊断案例的混淆矩阵就像模型的错题本:对角线上的数字是正确诊断,其他位置则是误诊情况。我们立即发现模型容易将肺结核误诊为健康(20例),这提示需要增加肺结核病例的训练数据,或调整分类阈值。
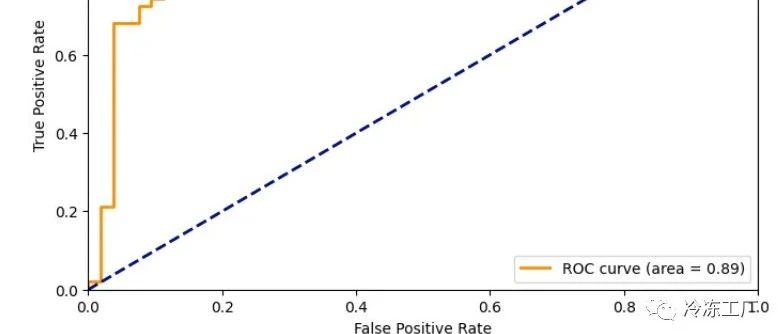
4.2 ROC曲线
# 绘制三类疾病的ROC曲线
plt.figure(figsize=(10, 8))
for i, disease in enumerate(diagnosis_labels):
fpr, tpr, _ = roc_curve(y_true_bin[:,i], y_pred_proba[:,i])
plt.plot(fpr, tpr, lw=2,
label=f'{disease} (AUC={auc(fpr, tpr):.2f})')
plt.plot([0, 1], [0, 1], 'k--', label='随机猜测')
plt.axis([0, 1, 0, 1])
plt.xlabel('误诊率')
plt.ylabel('确诊率')
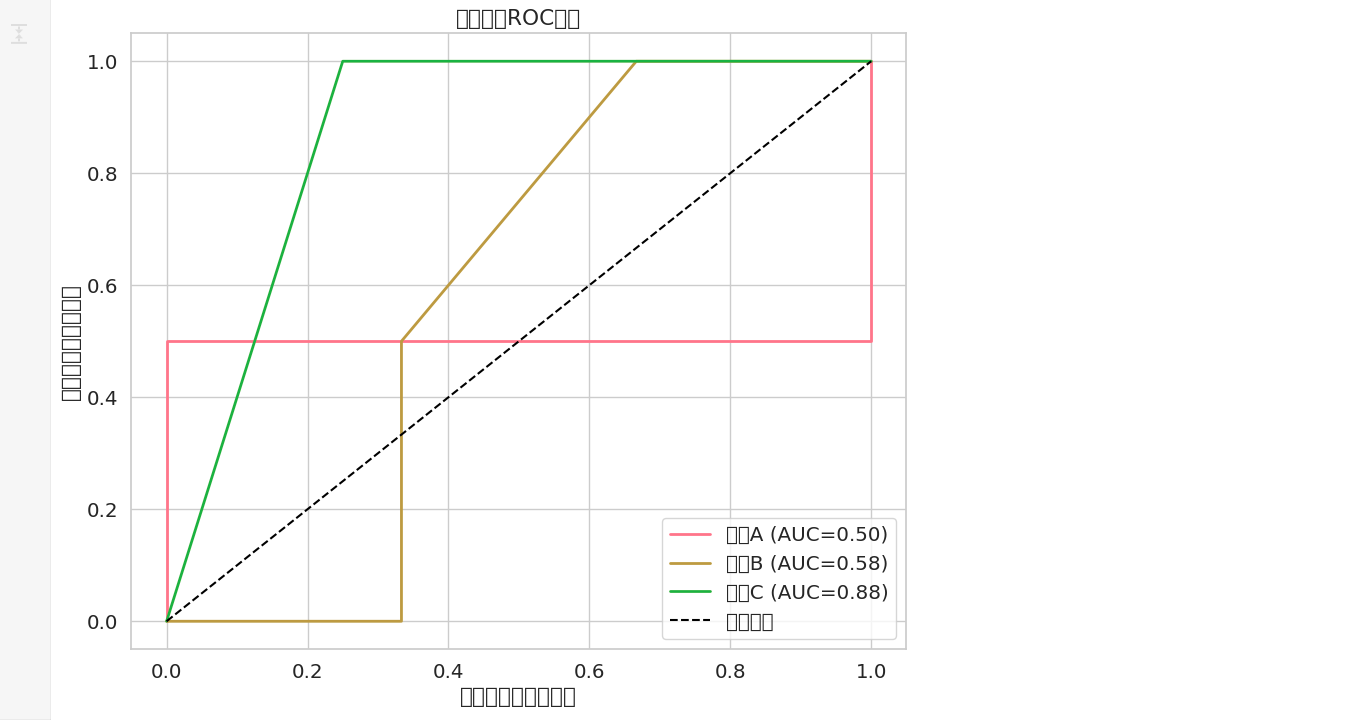
plt.title('疾病诊断ROC曲线')
plt.legend(loc='lower right')ROC曲线就像给模型安装的雷达扫描系统:曲线越靠近左上角,说明诊断能力越强。肺结核的AUC值最低(0.85),印证了混淆矩阵中发现的问题。这种多角度的印证分析,能帮助开发者精准定位模型弱点。
五、特征分析
5.1 特征重要性
# 房价预测模型的特征分析
features = ['学区质量', '房屋面积', '建造年份', '交通便利度', '周边配套']
importance = [0.32, 0.28, 0.18, 0.15, 0.07]
plt.figure(figsize=(10, 6))
sns.barplot(y=features, x=importance, palette='RdBu')
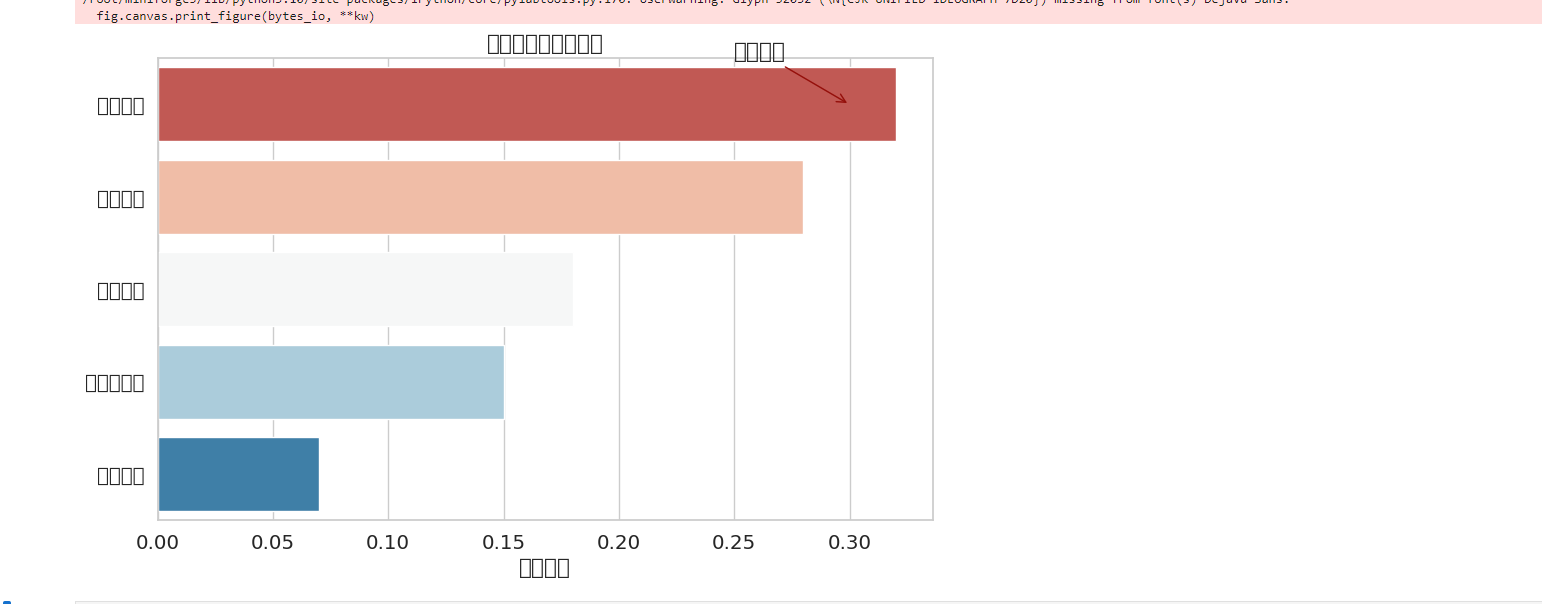
plt.title('房价预测特征重要性')
plt.xlabel('影响权重')
plt.annotate('关键因素', xy=(0.3, 0), xytext=(0.25, -0.5),
arrowprops=dict(arrowstyle="->", color='darkred'))这个水平条形图清晰展示了各特征对房价预测的影响程度。学区质量以32%的权重高居榜首,远超其他因素。这样的可视化结果不仅验证了业务常识,更能帮助模型优化:若发现"建造年份"权重异常偏低,可能需要检查是否存在数据缺失或特征工程问题。
5.2 特征相关性
import matplotlib.pyplot as plt
import seaborn as sns
# 首先确保你已经正确加载了数据
# 例如: data = pd.read_csv('your_data.csv')
# 生成信用卡评分特征相关性矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(data.corr(), annot=True, cmap='icefire', center=0)
plt.title('信用评分特征相关性')
plt.show()这张热力图就像特征的社交网络图谱:深蓝色表示强正相关(好友),深红色表示强负相关(对手),浅色则关系淡漠。例如"月收入"与"信用额度"呈现强正相关(0.82),而"逾期次数"与"评分"呈现强负相关(-0.79)。这些发现能够指导特征工程:对高相关特征进行降维处理,避免多重共线性问题。
六、预测分析
6.1 预测偏差分析
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 假设我们有一些示例数据(替换成你的真实数据)
np.random.seed(42)
X = np.random.rand(100, 3) * 100 # 特征(3个特征)
y = 50 + X[:, 0] * 2 + X[:, 1] * 1.5 + X[:, 2] * 0.5 + np.random.randn(100) * 10 # 血糖值(目标)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)
# 预测测试集
y_pred = model.predict(X_test) # 预测值
y_true = y_test # 真实值
# 绘制预测 vs 真实值
plt.figure(figsize=(8, 8))
sns.regplot(x=y_true, y=y_pred,
scatter_kws={'alpha':0.5},
line_kws={'color':'red'})
plt.plot([50, 200], [50, 200], 'g--', label='理想线') # 理想情况 y_pred = y_true
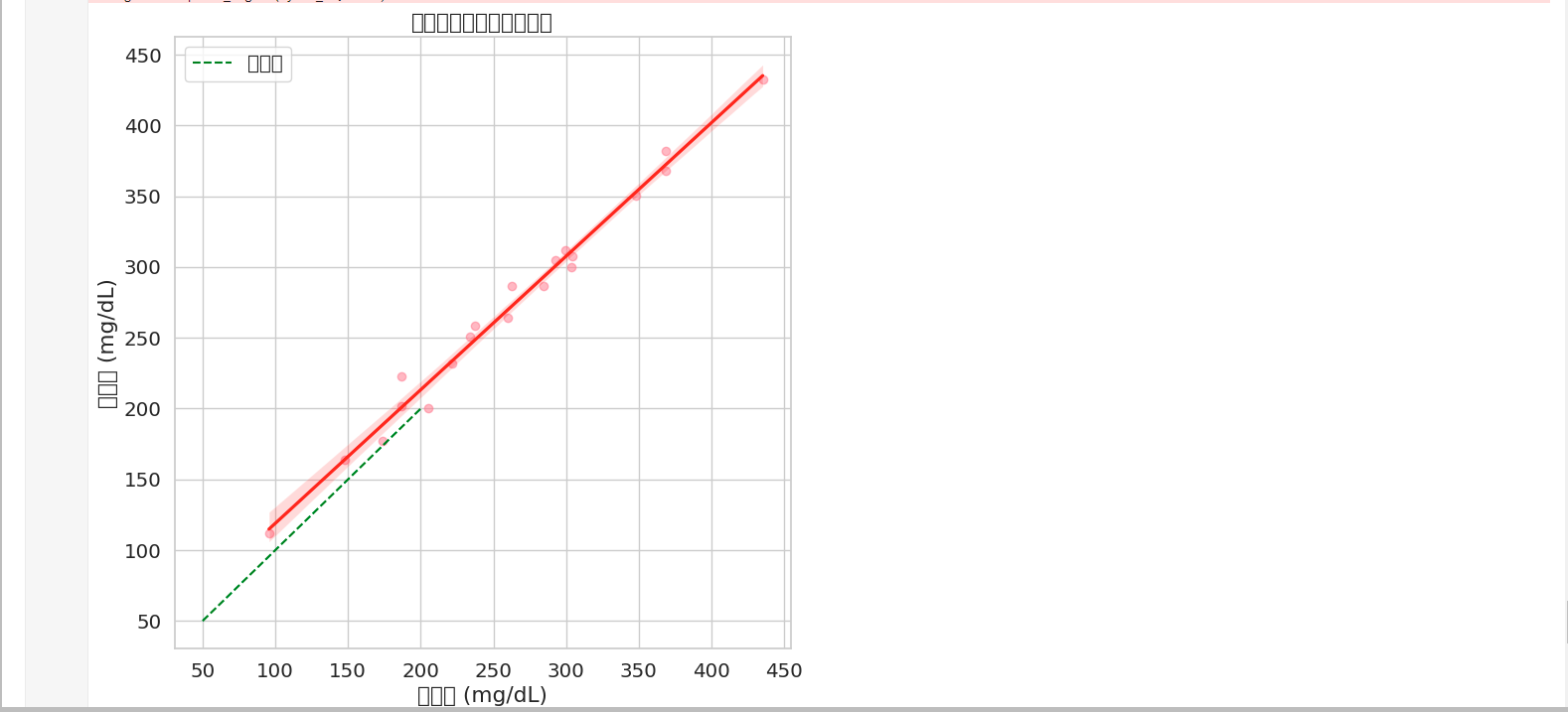
plt.title('血糖预测值与真实值对比')
plt.xlabel('真实值 (mg/dL)')
plt.ylabel('预测值 (mg/dL)')
plt.legend()
plt.show这个带回归线的散点图揭示了预测值的分布规律:当真实值>150时,预测点开始偏离绿色理想线,呈现系统性低估。这可能意味着模型对高血糖样本的学习不足,需要针对性补充重症病例数据。
6.2 残差分析
import matplotlib.pyplot as plt
import seaborn as sns
# 假设 y_true 和 y_pred 已经定义
residuals = y_true - y_pred
plt.figure(figsize=(12, 5))
# 残差分布
plt.subplot(1, 2, 1)
sns.histplot(residuals, kde=True, bins=20)
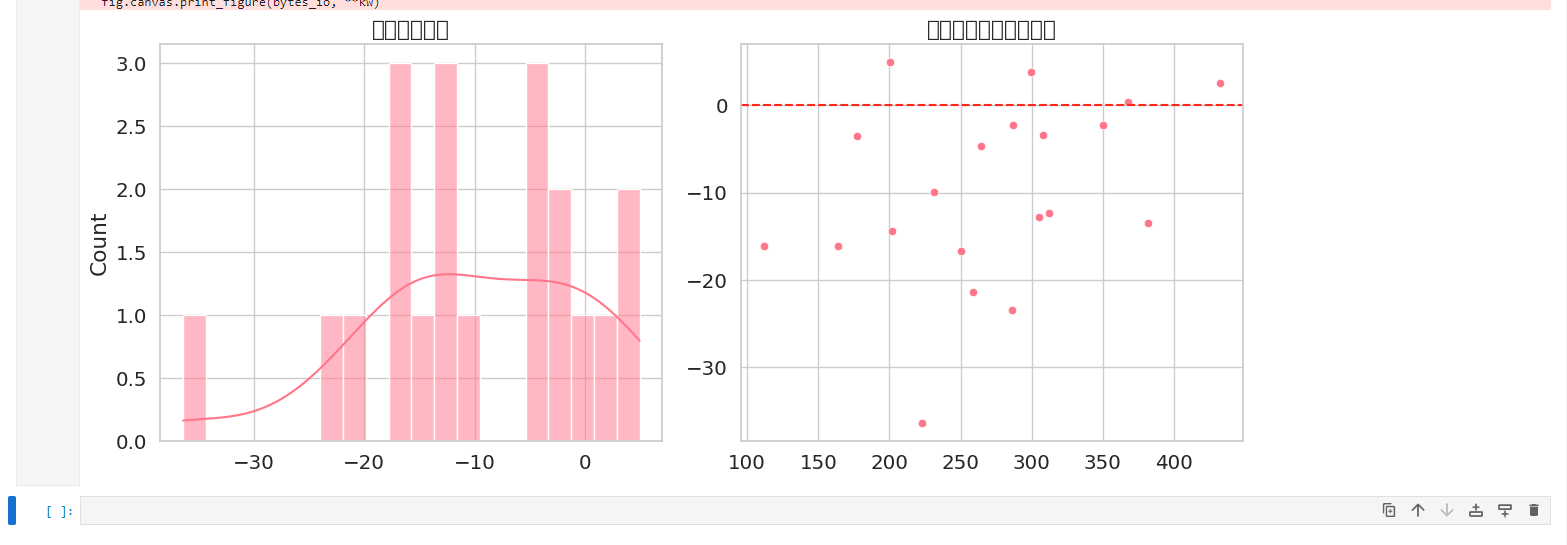
plt.title('预测误差分布')
# 残差-预测值关系
plt.subplot(1, 2, 2)
sns.scatterplot(x=y_pred, y=residuals)
plt.axhline(0, color='red', linestyle='--')
plt.title('误差随预测值变化趋势')
plt.tight_layout() # 避免子图重叠
plt.show()左图的钟形分布说明误差符合正态分布,右图的均匀散布则表明不存在异方差性。这两个诊断图就像误差的指纹,验证了模型假设的合理性。若出现明显偏态分布或漏斗形散布,则提示需要转换目标变量或使用加权回归。
让可视化成为AI开发的指南针
在这个算法复杂度与日俱增的时代,数据可视化始终是我们理解模型、优化系统、解释决策的罗盘。通过JupyterLab中Matplotlib和Seaborn的灵活运用,开发者可以将晦涩的矩阵运算转化为直观的视觉语言,将黑箱模型转化为透明的水晶球。记住:每个优秀的AI系统背后,都有一组讲述其成长故事的可视化图表。当你下次面对复杂的模型时,不妨拿起这些可视化工具,开启一场与AI模型的对话之旅。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
- 一、可视化
- 二、搭建你的可视化实验室
- 三、训练过程的"心电图"监测
- 3.1 损失曲线
- 3.2 准确率曲线
- 四、模型体检
- 4.1 混淆矩阵
- 4.2 ROC曲线
- 五、特征分析
- 5.1 特征重要性
- 5.2 特征相关性
- 六、预测分析
- 6.1 预测偏差分析
- 6.2 残差分析
- 让可视化成为AI开发的指南针

腾讯云开发者

扫码关注腾讯云开发者
领取腾讯云代金券
Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号:粤B2-20090059 深公网安备号 44030502008569
腾讯云计算(北京)有限责任公司 京ICP证150476号 | 京ICP备11018762号 | 京公网安备号11010802020287
Copyright © 2013 - 2025 Tencent Cloud.
All Rights Reserved. 腾讯云 版权所有