流苏管道中的QQ图
提问于 2019-11-21 13:35:56
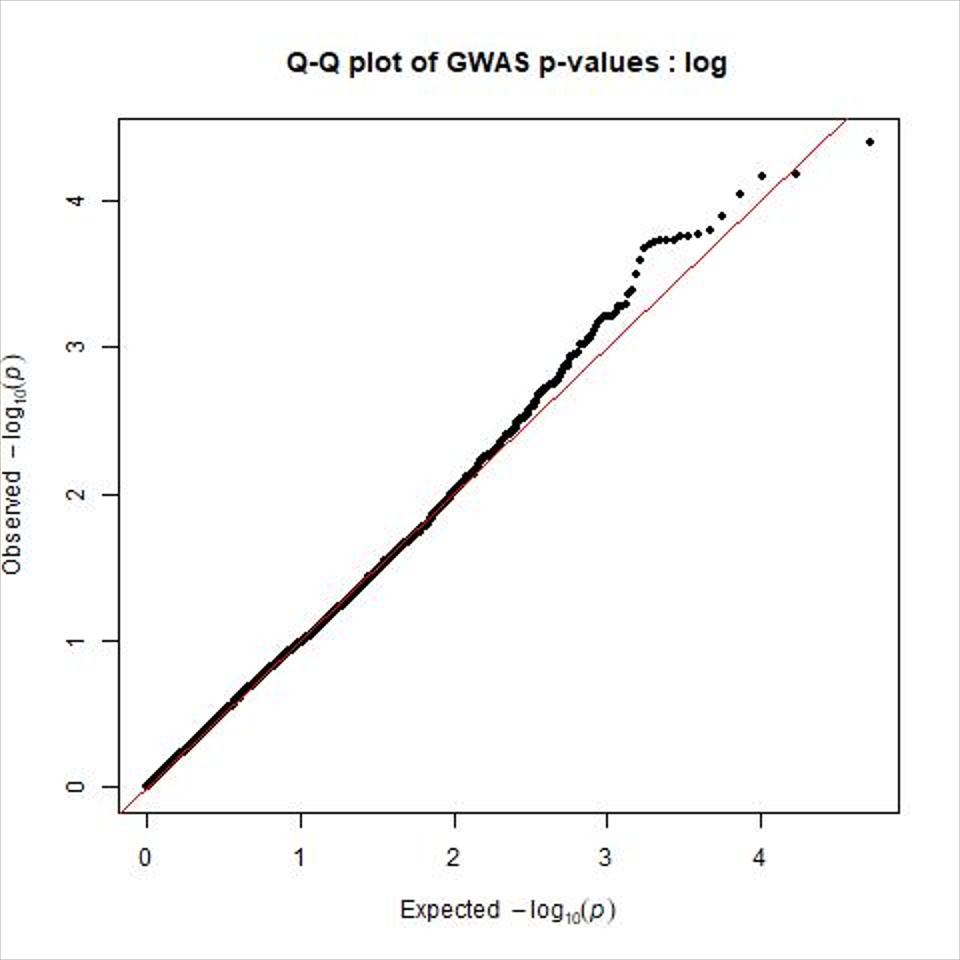
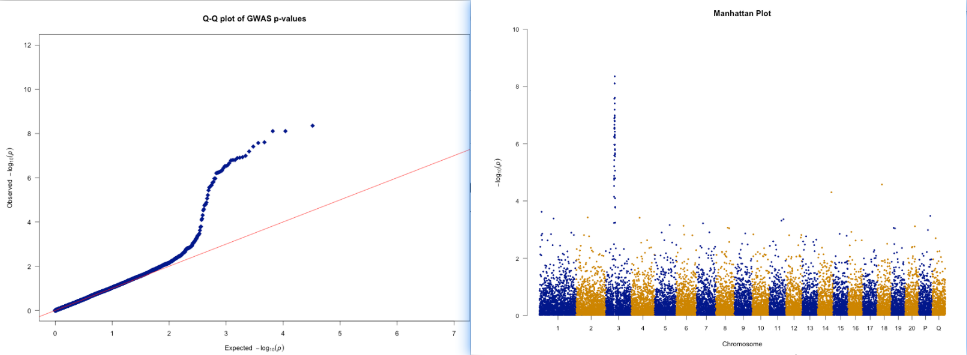
在我的GWAS分析中,我使用了流苏管道。在我的GWAS中,我正在研究两个相关的性状。我想在一个图中绘制两个性状的Q_Q图,就像我们可以从tassel程序中获得的那样

。
有没有人有什么建议,用哪一个r包可以做到这一点?使用qqman包中的qq()命令,我在单独的图中绘制QQ图,但我想要一个包含我的两个特征的图,就像我在Tassel中所做的那样
有什么建议吗?
回答 1
Stack Overflow用户
发布于 2019-11-21 14:44:03
在您的案例中,QQ图将您的结果的经验分布的分位数与如果零假设为真时理论上预期的分布的分位数进行比较。
如果你有n个数据点,比较n个分位数是有意义的,因为这样你的经验分布的实际分位数就是你的数据点,排序。
P值的理论分布是均匀分布。想想看,这正是它们存在的原因。例如,如果一个测量值被指定为p值0.05,那么如果您经常重复该实验,那么在您的实验中,仅有5%的实验中会出现这种或更极端的测量(零假设)。预计在50%的情况下,使用p=0.5进行测量。因此,推广到任意值p,你的累积分布函数
CDF( p ) =p具有≤的p值p=p的测量。
在维基百科中,这是0到1之间均匀分布的CDF。
因此,您的QQ图的预期n分位数是{1/n,2/n,...n/n}。(它们表示零假设为真的情况)
现在,我们有了理论分位数(x轴)和实际分位数。在R代码中,这类似于
expected_quantiles <- function(pvalues){
n = length(pvalues)
actual_quantiles = sort(pvalues)
expected_quantiles = seq_along(pvalues)/n
data.frame(expected = expected_quantiles, actual = actual_quantiles)
}您可以获取这些值的-log10并绘制它们,例如
testdata1 <- c(runif(98,0,1), 1e-4, 2e-5)
testdata2 <- c(runif(96,0,1), 1e-3, 2e-3, 2e-4)
qq <- lapply(list(d1 = testdata1, d2 = testdata2), expected_quantiles)
xlim <- rev(-log10(range(rbind(qq$d1, qq$d2)$expected))) * c(1, 1.1)
ylim <- rev(-log10(range(rbind(qq$d1, qq$d2)$actual))) * c(1, 1.1)
plot(NULL, xlim = xlim, ylim = ylim)
points(x = -log10(qq$d1$expected) ,y = -log10(qq$d1$actual), col = "red")
points(x = -log10(qq$d2$expected) ,y = -log10(qq$d2$actual), col = "blue")
abline(a = 0, b = 1)页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/58976316
复制